1 Introduction
Many tutorials on programming with dependent types define the type of length-indexed lists, also known as vectors. Using a language such as Agda (Norell, Reference Norell2007), we can write:
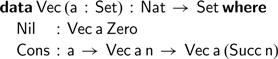
Many familiar functions on lists can be readily adapted to work on vectors, such as concatenation:
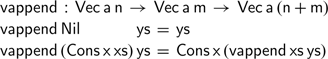
Here, the definitions of both addition and concatenation proceed by induction on the first argument; this coincidence allows concatenation to type check, without having to write explicit proofs involving natural numbers. Programming languages such as Agda will happily expand definitions while type checking—but any non-trivial equality between natural numbers may require further manual proofs.
However, not all functions on lists are quite so easy to adapt to vectors. How should we reverse a vector? There is an obvious—but inefficient—definition.
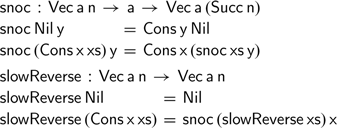
The
![]() $\textsf{snoc}$
function traverses a vector, adding a new element at its end. Repeatedly traversing the intermediate results constructed during reversal yields a function that is quadratic in the input vector’s length. Fortunately, there is a well-known solution using an accumulating parameter, often attributed to Hughes (Reference Hughes1986). If we try to implement this version of the reverse function on vectors, we get stuck quickly:
$\textsf{snoc}$
function traverses a vector, adding a new element at its end. Repeatedly traversing the intermediate results constructed during reversal yields a function that is quadratic in the input vector’s length. Fortunately, there is a well-known solution using an accumulating parameter, often attributed to Hughes (Reference Hughes1986). If we try to implement this version of the reverse function on vectors, we get stuck quickly:
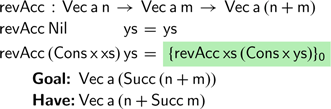
Here we have highlighted the unfinished part of the program, followed by the type of the value that we are trying to produce and the type of the expression that we have written so far. Each of these goals that appear in the text will be numbered, starting from
![]() $\textsf{0}$
here. In the case for non-empty lists, the recursive call
$\textsf{0}$
here. In the case for non-empty lists, the recursive call
![]() $\textsf{revAcc}\;\textsf{xs}\;(\textsf{Cons}\;\textsf{x}\;\textsf{ys})$
returns a vector of length
$\textsf{revAcc}\;\textsf{xs}\;(\textsf{Cons}\;\textsf{x}\;\textsf{ys})$
returns a vector of length
![]() $\textsf{n}\;\textsf{+}\;\textsf{Succ}\;\textsf{m}$
, whereas the function’s type signature requires a vector of length
$\textsf{n}\;\textsf{+}\;\textsf{Succ}\;\textsf{m}$
, whereas the function’s type signature requires a vector of length
![]() $(\textsf{Succ}\;\textsf{n})\;\textsf{+}\;\textsf{m}$
. Addition is typically defined by induction over its first argument, immediately producing an outermost successor when possible—correspondingly, the definition of
$(\textsf{Succ}\;\textsf{n})\;\textsf{+}\;\textsf{m}$
. Addition is typically defined by induction over its first argument, immediately producing an outermost successor when possible—correspondingly, the definition of
![]() $\textsf{vappend}$
type checks directly—but
$\textsf{vappend}$
type checks directly—but
![]() $\textsf{revAcc}$
does not.
$\textsf{revAcc}$
does not.
We can remedy this by defining a variation of addition that mimics the accumulating recursion of the
![]() $\textsf{revAcc}$
function:
$\textsf{revAcc}$
function:
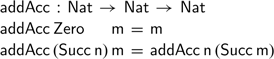
Using this accumulating addition, we can define the accumulating vector reversal function directly:
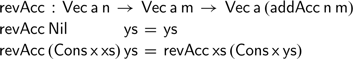
When we try to use the
![]() $\textsf{revAcc}$
function to define the top-level
$\textsf{revAcc}$
function to define the top-level
![]() $\textsf{vreverse}$
function; however, we run into a new problem:
$\textsf{vreverse}$
function; however, we run into a new problem:

Again, the desired definition does not type check:
![]() $\textsf{revAcc}\;\textsf{xs}\;\textsf{Nil}$
produces a vector of length
$\textsf{revAcc}\;\textsf{xs}\;\textsf{Nil}$
produces a vector of length
![]() $\textsf{addAcc}\;\textsf{n}\;\textsf{Zero}$
, whereas a vector of length
$\textsf{addAcc}\;\textsf{n}\;\textsf{Zero}$
, whereas a vector of length
![]() $\textsf{n}$
is required. We could try another variation of addition that pattern matches on its second argument, but this will break the first clause of the
$\textsf{n}$
is required. We could try another variation of addition that pattern matches on its second argument, but this will break the first clause of the
![]() $\textsf{revAcc}$
function. To complete the definition of vector reverse, we can use an explicit proof to coerce the right-hand side,
$\textsf{revAcc}$
function. To complete the definition of vector reverse, we can use an explicit proof to coerce the right-hand side,
![]() $\textsf{revAcc}\;\textsf{xs}\;\textsf{Nil}$
, to have the desired length. To do so, we define an auxiliary function that coerces a vector of length
$\textsf{revAcc}\;\textsf{xs}\;\textsf{Nil}$
, to have the desired length. To do so, we define an auxiliary function that coerces a vector of length
![]() $\textsf{n}$
into a vector of length
$\textsf{n}$
into a vector of length
![]() $\textsf{m}$
, provided that we can prove that
$\textsf{m}$
, provided that we can prove that
![]() $\textsf{n}$
and
$\textsf{n}$
and
![]() $\textsf{m}$
are equal:
$\textsf{m}$
are equal:
Using this function, we can now complete the definition of
![]() $\textsf{vreverse}$
as follows:
$\textsf{vreverse}$
as follows:
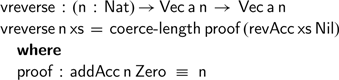
We have omitted the definition of
![]() $\textsf{proof}$
—but we will return to this point in the final section.
$\textsf{proof}$
—but we will return to this point in the final section.
This definition of
![]() $\textsf{vreverse}$
is certainly correct—but the additional coercion will clutter any subsequent lemmas that refer to this definition. To prove any property of
$\textsf{vreverse}$
is certainly correct—but the additional coercion will clutter any subsequent lemmas that refer to this definition. To prove any property of
![]() $\textsf{vreverse}$
will require pattern matching on the
$\textsf{vreverse}$
will require pattern matching on the
![]() $\textsf{proof}$
to reduce—rather than reasoning by induction on the vector directly.
$\textsf{proof}$
to reduce—rather than reasoning by induction on the vector directly.
Unfortunately, it is not at all obvious how to complete this definition without such proofs. We seem to have reached an impasse: how can we possibly define addition in such a way that
![]() $\textsf{Zero}$
is both a left and a right identity?
$\textsf{Zero}$
is both a left and a right identity?
2 Monoids and endofunctions
The solution can also be found in Hughes’s article, that explores using an alternative representation of lists known as difference lists. These difference lists identify a list with the partial application of the append function. Rather than work with natural numbers directly, we choose an alternative representation of natural numbers that immediately satisfies the desired monoidal equalities, representing a number as the partial application of addition.
In what follows, we will refer to these functions
![]() $\textsf{Nat}\;\to \;\textsf{Nat}$
as difference naturals. We can readily define the following conversions between natural numbers and difference naturals:
$\textsf{Nat}\;\to \;\textsf{Nat}$
as difference naturals. We can readily define the following conversions between natural numbers and difference naturals:

We have some choice of how to define the
![]() $\textsf{reify}$
function. As addition is defined by induction on the first argument, we define
$\textsf{reify}$
function. As addition is defined by induction on the first argument, we define
![]() $\textsf{reify}$
by applying
$\textsf{reify}$
by applying
![]() $\textsf{Zero}$
to its argument. This choice ensures that the desired ‘return trip’ property between our two representations of naturals holds definitionally:
$\textsf{Zero}$
to its argument. This choice ensures that the desired ‘return trip’ property between our two representations of naturals holds definitionally:
Note that we have chosen to use the type
![]() $\textsf{Nat}\;\to \;\textsf{Nat}$
here, but there is nothing specific about natural numbers in these definitions. These definitions can be readily adapted to work for any monoid—an observation we will explore further in later sections. Indeed, this is an instance of Cayley’s theorem for groups (Armstrong, Reference Armstrong1988, Chapter 8), or the Yoneda embedding more generally (Boisseau & Gibbons, Reference Boisseau and Gibbons2018; Awodey, Reference Awodey2010), that establishes an equivalence between the elements of a group and the partial application of the group’s multiplication operation.
$\textsf{Nat}\;\to \;\textsf{Nat}$
here, but there is nothing specific about natural numbers in these definitions. These definitions can be readily adapted to work for any monoid—an observation we will explore further in later sections. Indeed, this is an instance of Cayley’s theorem for groups (Armstrong, Reference Armstrong1988, Chapter 8), or the Yoneda embedding more generally (Boisseau & Gibbons, Reference Boisseau and Gibbons2018; Awodey, Reference Awodey2010), that establishes an equivalence between the elements of a group and the partial application of the group’s multiplication operation.
While this fixes the conversion between numbers and their representation using functions, we still need to define the monoidal operations on this representation. Just as for difference lists, the zero and addition operation correspond to the identity function and function composition, respectively:
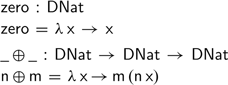
Somewhat surprisingly, all three monoid laws hold definitionally using this functional representation of natural numbers:
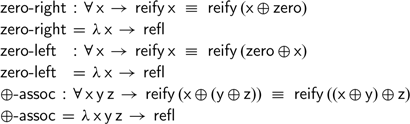
As adding zero corresponds to applying the identity function and addition is mapped to function composition, the proof of these equalities follows immediately after evaluating the left- and right-hand sides of the equality.
To convince ourselves that our definition of addition is correct, we should also prove the following lemma, stating that addition on ‘difference naturals’ and natural numbers agree for all inputs:
After simplifying both sides of the equation, the proof boils down to the associativity of addition. Proving this requires a simple inductive argument, and does not hold definitionally. The reverse function we will construct, however, does not rely on this property.
3 Revisiting reverse
Before we try to redefine our accumulating reverse function, we need one additional auxiliary definition. Besides
![]() $\textsf{zero}$
and the
$\textsf{zero}$
and the
![]() $ \oplus $
operation on these naturals—we will need a successor function to account for new elements added to the accumulating parameter. Given that
$ \oplus $
operation on these naturals—we will need a successor function to account for new elements added to the accumulating parameter. Given that
![]() $\textsf{Cons}$
constructs a vector of length
$\textsf{Cons}$
constructs a vector of length
![]() $\textsf{Succ}\;\textsf{n}$
for some
$\textsf{Succ}\;\textsf{n}$
for some
![]() $\textsf{n}$
, our first attempt at defining the successor operation on difference naturals becomes
$\textsf{n}$
, our first attempt at defining the successor operation on difference naturals becomes
With this definition in place, we can now fix the type of our accumulating reverse function:
As we want to define
![]() $\textsf{revAcc}$
by induction over its first argument vector, we choose that vector to have length
$\textsf{revAcc}$
by induction over its first argument vector, we choose that vector to have length
![]() $\textsf{n}$
, for some natural number
$\textsf{n}$
, for some natural number
![]() $\textsf{n}$
. Attempting to pattern match on a vector of length
$\textsf{n}$
. Attempting to pattern match on a vector of length
![]() $\textsf{reify}\;\textsf{m}$
creates unification problems that Agda cannot resolve: it cannot decide which constructors of the
$\textsf{reify}\;\textsf{m}$
creates unification problems that Agda cannot resolve: it cannot decide which constructors of the
![]() $\textsf{Vec}$
datatype can be used to construct a vector of length
$\textsf{Vec}$
datatype can be used to construct a vector of length
![]() $\textsf{reify}\;\textsf{m}$
. As a result, we index the first argument vector by a
$\textsf{reify}\;\textsf{m}$
. As a result, we index the first argument vector by a
![]() $\textsf{Nat}$
; the second argument vector has length
$\textsf{Nat}$
; the second argument vector has length
![]() $\textsf{reify}\;\textsf{m}$
, for some
$\textsf{reify}\;\textsf{m}$
, for some
![]() $\textsf{m}\;\mathbin{:}\;\textsf{DNat}$
. The length of the vector returned by
$\textsf{m}\;\mathbin{:}\;\textsf{DNat}$
. The length of the vector returned by
![]() $\textsf{revAcc}$
is the sum of the input lengths—
$\textsf{revAcc}$
is the sum of the input lengths—
![]() ${\rm{reify}}\;(\left[\kern-0.15em\left[ {\rm{n}} \right]\kern-0.15em\right]\; \oplus \;{\rm{m}})$
—which simplifies to
${\rm{reify}}\;(\left[\kern-0.15em\left[ {\rm{n}} \right]\kern-0.15em\right]\; \oplus \;{\rm{m}})$
—which simplifies to
![]() $\textsf{m}\;\textsf{n}$
. We can now attempt to complete the definition as follows:
$\textsf{m}\;\textsf{n}$
. We can now attempt to complete the definition as follows:
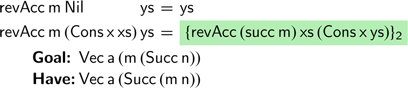
Unfortunately, the desired definition does not type check. The right-hand side produces a vector of the wrong length. To understand why, compare the types of the goal and expression we have produced. Using this definition of
![]() $\textsf{succ}$
creates an outermost successor constructor, hence we cannot produce a vector of the right type.
$\textsf{succ}$
creates an outermost successor constructor, hence we cannot produce a vector of the right type.
Let us not give up just yet. We can still redefine our successor operation as follows:
This definition should avoid the problem that arises from the outermost
![]() $\textsf{Succ}$
constructor that we observed previously. If we now attempt to complete the definition of
$\textsf{Succ}$
constructor that we observed previously. If we now attempt to complete the definition of
![]() $\textsf{revAcc}$
, we encounter a different problem:
$\textsf{revAcc}$
, we encounter a different problem:
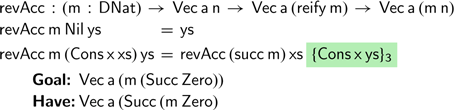
Once again, the problem lies in the case for
![]() $\textsf{Cons}$
. We would like to make a tail recursive call on the remaining list
$\textsf{Cons}$
. We would like to make a tail recursive call on the remaining list
![]() $\textsf{xs}$
, passing
$\textsf{xs}$
, passing
![]() $\textsf{succ}\;\textsf{m}$
as the length of the accumulating parameter. This call now type checks—as the desired length
$\textsf{succ}\;\textsf{m}$
as the length of the accumulating parameter. This call now type checks—as the desired length
![]() $\textsf{m}\;(\textsf{Succ}\;\textsf{n})$
and computed length
$\textsf{m}\;(\textsf{Succ}\;\textsf{n})$
and computed length
![]() $(\textsf{succ}\;\textsf{m})\;\textsf{n}$
coincide. The problem, however, lies in constructing the accumulating parameter to pass to the recursive call. The recursive call requires a vector of length
$(\textsf{succ}\;\textsf{m})\;\textsf{n}$
coincide. The problem, however, lies in constructing the accumulating parameter to pass to the recursive call. The recursive call requires a vector of length
![]() $\textsf{m}\;(\textsf{Succ}\;\textsf{Zero})$
, whereas the
$\textsf{m}\;(\textsf{Succ}\;\textsf{Zero})$
, whereas the
![]() $\textsf{Cons}$
constructor used here returns a vector of length
$\textsf{Cons}$
constructor used here returns a vector of length
![]() $\textsf{Succ}\;(\textsf{m}\;\textsf{Zero})$
.
$\textsf{Succ}\;(\textsf{m}\;\textsf{Zero})$
.
We might try to define an auxiliary function, analogous to the
![]() $\textsf{Cons}$
constructor:
$\textsf{Cons}$
constructor:
If we try to define this function directly, however, we get stuck immediately. The type requires that we produce a vector of length,
![]() $\textsf{m}\;(\textsf{Succ}\;\textsf{Zero})$
. Without knowing anything further about
$\textsf{m}\;(\textsf{Succ}\;\textsf{Zero})$
. Without knowing anything further about
![]() $\textsf{m}$
, we cannot even decide if the vector should be empty or not. Fortunately, we do know more about the difference natural
$\textsf{m}$
, we cannot even decide if the vector should be empty or not. Fortunately, we do know more about the difference natural
![]() $\textsf{m}$
in the definition of
$\textsf{m}$
in the definition of
![]() $\textsf{revAcc}$
. Initially, our accumulator will be empty—hence
$\textsf{revAcc}$
. Initially, our accumulator will be empty—hence
![]() $\textsf{m}$
will be the identity function. In each iteration of
$\textsf{m}$
will be the identity function. In each iteration of
![]() $\textsf{revAcc}$
, we will compose
$\textsf{revAcc}$
, we will compose
![]() $\textsf{m}$
with an additional
$\textsf{m}$
with an additional
![]() $\textsf{succ}$
until our input vector is empty.
$\textsf{succ}$
until our input vector is empty.
If we assume we are provided with a
![]() $\textsf{cons}$
function of the right type, we can complete the definition of vector reverse as expected:
$\textsf{cons}$
function of the right type, we can complete the definition of vector reverse as expected:
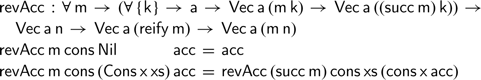
This definition closely follows our previous attempt. Rather than applying the
![]() $\textsf{Cons}$
constructor, this definition uses the argument
$\textsf{Cons}$
constructor, this definition uses the argument
![]() $\textsf{cons}$
function to extend the accumulating parameter. Here, the
$\textsf{cons}$
function to extend the accumulating parameter. Here, the
![]() $\textsf{cons}$
function is assumed to commute with the successor constructor and an arbitrary difference natural
$\textsf{cons}$
function is assumed to commute with the successor constructor and an arbitrary difference natural
![]() $\textsf{m}$
. In the recursive call, the first argument vector has length
$\textsf{m}$
. In the recursive call, the first argument vector has length
![]() $\textsf{n}$
, whereas the second has length
$\textsf{n}$
, whereas the second has length
![]() $\textsf{reify}\;(\textsf{succ}\;\textsf{m})$
. As the
$\textsf{reify}\;(\textsf{succ}\;\textsf{m})$
. As the
![]() $\textsf{cons}$
parameter extends a vector of length
$\textsf{cons}$
parameter extends a vector of length
![]() $\textsf{m}\;\textsf{k}$
for any
$\textsf{m}\;\textsf{k}$
for any
![]() $\textsf{k}$
, we use it in our recursive call, silently incrementing the implicit argument passed to
$\textsf{k}$
, we use it in our recursive call, silently incrementing the implicit argument passed to
![]() $\textsf{cons}$
. In this way, we count down from
$\textsf{cons}$
. In this way, we count down from
![]() $\textsf{n}$
, the length of the first vector, whilst incrementing the difference natural
$\textsf{n}$
, the length of the first vector, whilst incrementing the difference natural
![]() $\textsf{m}$
in each recursive call.
$\textsf{m}$
in each recursive call.
But how are we ever going to call this function? We have already seen that it is impossible to define the
![]() $\textsf{cons}$
function in general. Yet we do not need to define
$\textsf{cons}$
function in general. Yet we do not need to define
![]() $\textsf{cons}$
for arbitrary values of
$\textsf{cons}$
for arbitrary values of
![]() $\textsf{m}$
—we only ever call the
$\textsf{m}$
—we only ever call the
![]() $\textsf{revAcc}$
function from the
$\textsf{revAcc}$
function from the
![]() $\textsf{vreverse}$
function with an accumulating parameter that is initially empty. As a result, we only need to concern ourselves with the case that
$\textsf{vreverse}$
function with an accumulating parameter that is initially empty. As a result, we only need to concern ourselves with the case that
![]() $\textsf{m}$
is
$\textsf{m}$
is
![]() $\textsf{zero}$
—or rather, the identity function. When
$\textsf{zero}$
—or rather, the identity function. When
![]() $\textsf{m}$
is the identity function, the type of the
$\textsf{m}$
is the identity function, the type of the
![]() $\textsf{cons}$
function required simply becomes:
$\textsf{cons}$
function required simply becomes:
Hence, it suffices to pass the
![]() $\textsf{Cons}$
constructor to
$\textsf{Cons}$
constructor to
![]() $\textsf{revAcc}$
after all:
$\textsf{revAcc}$
after all:
This completes the first proof-free reconstruction of vector reverse.
Correctness
Reasoning about this definition of vector reverse, however, is a rather subtle affair. Suppose we want to prove
![]() $\textsf{vreverse}$
is equal to the quadratic
$\textsf{vreverse}$
is equal to the quadratic
![]() $\textsf{slowReverse}$
function from the introduction:
$\textsf{slowReverse}$
function from the introduction:
If we try to prove this using induction on
![]() $\textsf{xs}$
directly, we quickly get stuck in the case for non-empty vectors: we cannot use our induction hypothesis, as the definition of
$\textsf{xs}$
directly, we quickly get stuck in the case for non-empty vectors: we cannot use our induction hypothesis, as the definition of
![]() $\textsf{vreverse}$
assumes that the accumulator is the empty vector. To fix this, we need to formulate and prove a more general statement about calls to
$\textsf{vreverse}$
assumes that the accumulator is the empty vector. To fix this, we need to formulate and prove a more general statement about calls to
![]() $\textsf{revAcc}$
with an arbitrary accumulator, corresponding to a lemma of the following form:
$\textsf{revAcc}$
with an arbitrary accumulator, corresponding to a lemma of the following form:
Here the
![]() $\textsf{vappend}$
function refers to the append on vectors, defined in the introduction. There is a problem, however, formulating such a lemma: the
$\textsf{vappend}$
function refers to the append on vectors, defined in the introduction. There is a problem, however, formulating such a lemma: the
![]() $\textsf{vappend}$
function uses the usual addition operation in its type, rather than the ‘difference addition’ used by
$\textsf{vappend}$
function uses the usual addition operation in its type, rather than the ‘difference addition’ used by
![]() $\textsf{revAcc}$
. As a result, the vectors on both sides of the equality sign have different types. To fix this, we need the following variant of
$\textsf{revAcc}$
. As a result, the vectors on both sides of the equality sign have different types. To fix this, we need the following variant of
![]() $\textsf{vappend}$
, where the length of the second vector is represented by a difference natural:
$\textsf{vappend}$
, where the length of the second vector is represented by a difference natural:
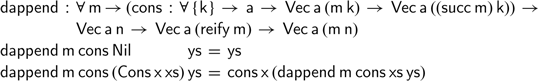
Using this ‘difference append’ operation, we can now formulate and prove the following correctness property, stating that
![]() $\textsf{revAcc}$
pushes all the elements of
$\textsf{revAcc}$
pushes all the elements of
![]() $\textsf{xs}$
onto the accumulating parameter
$\textsf{xs}$
onto the accumulating parameter
![]() $\textsf{ys}$
:
$\textsf{ys}$
:
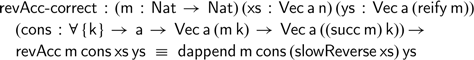
The proof itself proceeds by induction on the vector
![]() $\textsf{xs}$
and requires a single auxiliary lemma relating
$\textsf{xs}$
and requires a single auxiliary lemma relating
![]() $\textsf{dappend}$
and
$\textsf{dappend}$
and
![]() $\textsf{snoc}$
. Using
$\textsf{snoc}$
. Using
![]() $\textsf{revAcc-correct}$
and the fact that
$\textsf{revAcc-correct}$
and the fact that
![]() $\textsf{Nil}$
is the right-unit of
$\textsf{Nil}$
is the right-unit of
![]() $\textsf{dappend}$
, we can now complete the proof of
$\textsf{dappend}$
, we can now complete the proof of
![]() $\textsf{vreverse-correct}$
.
$\textsf{vreverse-correct}$
.
4 Using a left fold
The version of vector reverse defined in the Agda standard library uses a left fold. In this section, we will reconstruct this definition. A first attempt might use the following type for the
![]() $\textsf{fold}$
on vectors:
$\textsf{fold}$
on vectors:
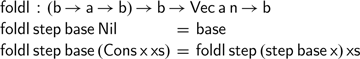
Unfortunately, we cannot define
![]() $\textsf{vreverse}$
using this fold. The first argument,
$\textsf{vreverse}$
using this fold. The first argument,
![]() $\textsf{f}$
, of
$\textsf{f}$
, of
![]() $\textsf{foldl}$
has type
$\textsf{foldl}$
has type
![]() $\textsf{b}\;\to \;\textsf{a}\;\to \;\textsf{b}$
; we would like to pass the
$\textsf{b}\;\to \;\textsf{a}\;\to \;\textsf{b}$
; we would like to pass the
![]() $\textsf{flip}\;\textsf{Cons}$
function as this first argument, but it has type
$\textsf{flip}\;\textsf{Cons}$
function as this first argument, but it has type
![]() $\textsf{Vec}\;\textsf{a}\;\textsf{n}\;\to \;\textsf{a}\;\to \;\textsf{Vec}\;\textsf{a}\;(\textsf{Succ}\;\textsf{n})$
—which will not type check as the first argument and return type are not identical. We can solve this, by generalising the type of this function slightly, indexing the return type
$\textsf{Vec}\;\textsf{a}\;\textsf{n}\;\to \;\textsf{a}\;\to \;\textsf{Vec}\;\textsf{a}\;(\textsf{Succ}\;\textsf{n})$
—which will not type check as the first argument and return type are not identical. We can solve this, by generalising the type of this function slightly, indexing the return type
![]() $\textsf{b}$
by a natural number:
$\textsf{b}$
by a natural number:
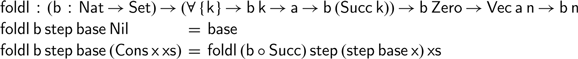
At heart, this definition is the same as the one above. There is one important distinction: the return type changes in each recursive call by precomposing with the successor constructor. In a way, this ‘reverses’ the natural number, as the outermost successor is mapped to the innermost successor in the type of the result. The accumulating nature of the
![]() $\textsf{foldl}$
is reflected in how the return type changes across recursive calls.
$\textsf{foldl}$
is reflected in how the return type changes across recursive calls.
We can use this version of
![]() $\textsf{foldl}$
to define a simple vector reverse:
$\textsf{foldl}$
to define a simple vector reverse:
This definition does not require any further proofs: the calculation of the return type follows the exact same recursive pattern as the accumulating vector under construction.
The
![]() $\textsf{foldl}$
function on vectors is a useful abstraction for defining accumulating functions over vectors. For example, as Kidney (Reference Kidney2019) has shown we can define the convolution of two vectors in a single pass in the style of Danvy & Goldberg (Reference Danvy and Goldberg2005):
$\textsf{foldl}$
function on vectors is a useful abstraction for defining accumulating functions over vectors. For example, as Kidney (Reference Kidney2019) has shown we can define the convolution of two vectors in a single pass in the style of Danvy & Goldberg (Reference Danvy and Goldberg2005):
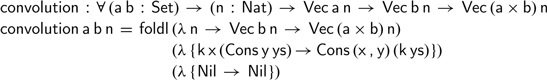
Monoids indexed by monoids
A similar problem—monoidal equalities in indices—shows up when trying to prove that vectors form a monoid. Where proving the monoidal laws for natural numbers or lists is a straightforward exercise for students learning Agda, vectors pose more of a challenge. Crucially, if the lengths of two vectors are not (definitionally) equal, the statement that the vectors themselves are equal is not even type correct. For example, given a vector
![]() $\textsf{xs}\;\mathbin{:}\;\textsf{Vec}\;\textsf{a}\;\textsf{n}$
, we might try to state the following equality:
$\textsf{xs}\;\mathbin{:}\;\textsf{Vec}\;\textsf{a}\;\textsf{n}$
, we might try to state the following equality:
The vector on the left-hand side of the equality has type
![]() ${\textsf{Vec}\;\textsf{a}\;\textsf{n}}$
, while the vector on the right-hand side has type
${\textsf{Vec}\;\textsf{a}\;\textsf{n}}$
, while the vector on the right-hand side has type
![]() ${\textsf{Vec}\;\textsf{a}\;(\textsf{n}\;\textsf{+}\;\textsf{0})}$
. As these two types are not the same—the vectors have different lengths—the statement of this equality is not type correct.
${\textsf{Vec}\;\textsf{a}\;(\textsf{n}\;\textsf{+}\;\textsf{0})}$
. As these two types are not the same—the vectors have different lengths—the statement of this equality is not type correct.
For difference vectors, however, this is not the case. To illustrate this, we begin by defining the type of difference vectors as follows:
We can then define the usual zero and addition operations on difference vectors as follows:
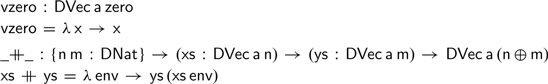
Next we can formulate the monoidal equalities and establish that these all hold trivially:
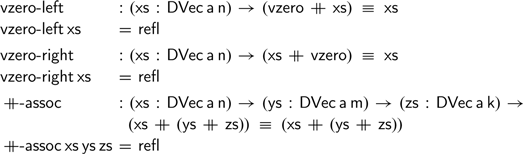
We have elided some implicit length arguments that Agda cannot infer automatically, but it should be clear that the monoidal operations on difference vectors are no different from the difference naturals we saw in Section 2.
It is worth pointing out that using the usual definitions of natural numbers and additions, the latter two definitions would not hold—a fortiori, the statement of the properties
![]() $\textsf{vzero-right}$
and
$\textsf{vzero-right}$
and
![]() $\mathbin{+\!\!\!+} \!\textsf{-assoc}$
would not even type check. Consider the type of
$\mathbin{+\!\!\!+} \!\textsf{-assoc}$
would not even type check. Consider the type of
![]() $\textsf{vzero-right}$
, for instance: formulating this property using natural numbers and addition would yield a vector on the left-hand side of the equation of length
$\textsf{vzero-right}$
, for instance: formulating this property using natural numbers and addition would yield a vector on the left-hand side of the equation of length
![]() $\textsf{n}\;\textsf{+}\;\textsf{0}$
, whereas
$\textsf{n}\;\textsf{+}\;\textsf{0}$
, whereas
![]() $\textsf{xs}$
has length
$\textsf{xs}$
has length
![]() $\textsf{n}$
. As the equality type can only be used to compare vectors of equal length, the statement of
$\textsf{n}$
. As the equality type can only be used to compare vectors of equal length, the statement of
![]() $\textsf{vzero-right}$
would be type incorrect. Addressing this requires coercing the lengths of the vectors involved—as we did in the very first definition of
$\textsf{vzero-right}$
would be type incorrect. Addressing this requires coercing the lengths of the vectors involved—as we did in the very first definition of
![]() $\textsf{vreverse}$
in the introduction—that quickly spreads throughout any subsequent definitions.
$\textsf{vreverse}$
in the introduction—that quickly spreads throughout any subsequent definitions.
In this section, we will explore another application of the Cayley representation of monoids. Instead of indexing by a natural number, this section revolves around computations indexed by lists.
We begin by defining a small language of boolean expressions:

The
![]() $\textsf{Expr}$
data type has constructors for truth, falsity, negation, conjunction and disjunction. Expressions are parametrised by a list of variables,
$\textsf{Expr}$
data type has constructors for truth, falsity, negation, conjunction and disjunction. Expressions are parametrised by a list of variables,
![]() $\textsf{vars}\;\mathbin{:}\;\textsf{List}\;\textsf{a}$
for some type
$\textsf{vars}\;\mathbin{:}\;\textsf{List}\;\textsf{a}$
for some type
![]() $\textsf{a}\;\mathbin{:}\;\textsf{Set}$
. While we could model a finite collection of variables using the well known
$\textsf{a}\;\mathbin{:}\;\textsf{Set}$
. While we could model a finite collection of variables using the well known
![]() $\textsf{Fin}$
type, we choose a slightly different representation here—allowing us to illustrate how the Cayley representation can be used for other indices beyond natural numbers. Each
$\textsf{Fin}$
type, we choose a slightly different representation here—allowing us to illustrate how the Cayley representation can be used for other indices beyond natural numbers. Each
![]() $\textsf{Var}$
constructor stores a proof,
$\textsf{Var}$
constructor stores a proof,
![]() ${\rm{x}}\; \in \;{\rm{vars}}$
, that is used to denote the particular named variable to which is being referred. The proofs,
${\rm{x}}\; \in \;{\rm{vars}}$
, that is used to denote the particular named variable to which is being referred. The proofs,
![]() $\textsf{x}\; \in \;\textsf{xs}$
, can be constructed using a pair of constructors,
$\textsf{x}\; \in \;\textsf{xs}$
, can be constructed using a pair of constructors,
![]() $\textsf{Top}$
and
$\textsf{Top}$
and
![]() $\textsf{Pop}$
, that refer to the elements in the head and tail of the list, respectively:
$\textsf{Pop}$
, that refer to the elements in the head and tail of the list, respectively:

Indexing expressions by the list of variables they may contain allows us to write a total evaluation function. The key idea is that our evaluator is passed an environment assigning a boolean value to each variable in our list:
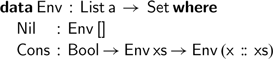
The evaluator itself is easy enough to define; it maps each constructor of the
![]() $\textsf{Expr}$
data type to its corresponding operation on booleans.
$\textsf{Expr}$
data type to its corresponding operation on booleans.

The only interesting case is the one for variables, where we call an auxiliary
![]() $\textsf{lookup}$
function to find the boolean value associated with the given variable.
$\textsf{lookup}$
function to find the boolean value associated with the given variable.
For a large fixed expression, however, we may not want to call
![]() $\textsf{eval}$
over and over again. Instead, it may be preferable to construct a decision tree associated with a given expression. The decision tree associated with an expression is a perfect binary tree, where each node branches over a single variable:
$\textsf{eval}$
over and over again. Instead, it may be preferable to construct a decision tree associated with a given expression. The decision tree associated with an expression is a perfect binary tree, where each node branches over a single variable:
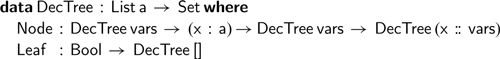
Given any environment, we can still ‘evaluate’ the boolean expression corresponding to the tree, using the environment to navigate to the unique leaf corresponding to the series of true-false choices for each variable:
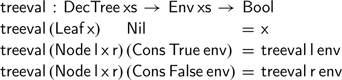
We would now like to write a function that converts a boolean expression into its decision tree representation, while maintaining the scope hygiene that our expression data type enforces. We could imagine trying to do so by induction on the list of free variables, repeatedly substituting the variables one by one:
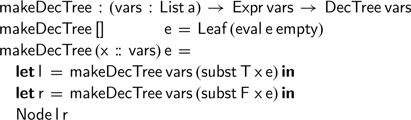
But this is not entirely satisfactory: to prove this function correct, we would need to prove various lemmas relating substitution and evaluation; furthermore, this function is inefficient, as it repeatedly traverses the expression to perform substitutions.
Instead, we would like to define an accumulating version of
![]() $\textsf{makeDecTree}$
, that carries around a (partial) environment of those variables on which we have already branched. As we shall see, this causes problems similar to those that we saw previously for reversing a vector. A first attempt might proceed by induction on the free variables in our expression, that have not yet been captured in our environment:
$\textsf{makeDecTree}$
, that carries around a (partial) environment of those variables on which we have already branched. As we shall see, this causes problems similar to those that we saw previously for reversing a vector. A first attempt might proceed by induction on the free variables in our expression, that have not yet been captured in our environment:

This definition, however, quickly gets stuck. In the recursive calls, the environment has grown, but the variables in the expression and environment no longer line up. The situation is similar to the very first attempt at defining the accumulating vector reverse function: the usual definition of addition is unsuitable for defining functions using an accumulating parameter. Fortunately, the solution is to define a function
![]() $\textsf{revAcc}$
, akin to the one defined for vectors, that operates on lists:
$\textsf{revAcc}$
, akin to the one defined for vectors, that operates on lists:
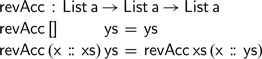
We can now attempt to construct the desired decision tree, using the
![]() $\textsf{revAcc}$
function in the type indices, as follows:
$\textsf{revAcc}$
function in the type indices, as follows:
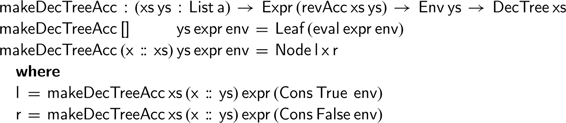
Although this definition now type checks, just as we saw for one of our previous attempts for
![]() $\textsf{revAcc}$
, the problem arises once we try to call this function with an initially empty environment:
$\textsf{revAcc}$
, the problem arises once we try to call this function with an initially empty environment:
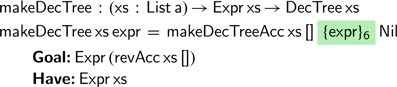
Calling the accumulating version fails to produce a value of the desired type—in particular, it produces a tree branching over the variables
![]() $\textsf{revAcc}\;\textsf{xs}\;\textsf{[]}$
rather than
$\textsf{revAcc}\;\textsf{xs}\;\textsf{[]}$
rather than
![]() $\textsf{xs}$
. To address this problem, however, we can move from an environment indexed by a regular lists to one indexed by a difference list, accumulating the values of the variables we have seen so far:
$\textsf{xs}$
. To address this problem, however, we can move from an environment indexed by a regular lists to one indexed by a difference list, accumulating the values of the variables we have seen so far:
Note that we use the Cayley representation of monoids in both the type index of and the value representing environments.
We can now complete our definition as expected, performing induction without ever having to prove a single equality about the concatenation of lists:

Finally, we can kick off our accumulating function with a pair of identity functions, corresponding to the zero elements of the list of variables that have been branched on and the difference environment:
Interestingly, the type signature of this top-level function does not mention the ‘difference environment’ or ‘difference lists’ at all.
Can we verify that definition is correct? The obvious theorem we may want to prove states the
![]() $\textsf{eval}$
and
$\textsf{eval}$
and
![]() $\textsf{treeval}$
functions agree on all possible expressions:
$\textsf{treeval}$
functions agree on all possible expressions:
A direct proof by induction quickly fails, as we cannot use our induction hypothesis; we can, however, prove a more general lemma that implies this result:
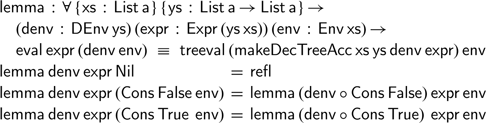
The proof is reassuringly simple; it has the same accumulating structure as the inductive definitions we have seen.
In this last section, we show how this technique of mapping monoids to their Cayley representation can be used to solve equalities between any monoidal expressions. To generalise the constructions we have seen so far, we define the following Agda record representing monoids:
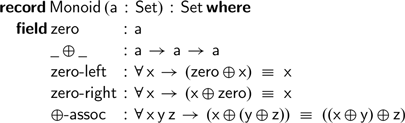
We can represent expressions built from the monoidal operations using the following data type,
![]() $\textsf{MExpr}$
:
$\textsf{MExpr}$
:
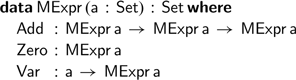
If we have a suitable monoid in scope, we can evaluate a monoidal expression,
![]() $\textsf{MExpr}$
, in the obvious fashion:
$\textsf{MExpr}$
, in the obvious fashion:
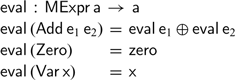
This is, however, not the only way to evaluate such expressions. As we have already seen, we can also define a pair of functions converting a monoidal expression to its Cayley representation and back:
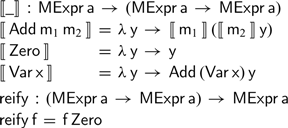
Finally, we can normalise any expression by composing these two functions:
Crucially, we can prove that this
![]() $\textsf{normalise}$
function preserves the (monoidal) semantics of our monoidal expressions:
$\textsf{normalise}$
function preserves the (monoidal) semantics of our monoidal expressions:
Where the cases for
![]() $\textsf{Zero}$
and
$\textsf{Zero}$
and
![]() $\textsf{Var}$
are straightforward, the addition case is more interesting. This final case requires a pair of auxiliary lemmas that rely on the monoid equalities:
$\textsf{Var}$
are straightforward, the addition case is more interesting. This final case requires a pair of auxiliary lemmas that rely on the monoid equalities:
Using transitivity, we can complete this last case of the proof.
Finally, we can use this soundness result to prove that two expressions are equal under evaluation, provided their corresponding normalised expressions are equal under evaluation:
What have we gained? On the surface, these general constructions may not seem particularly useful or exciting. Yet the
![]() $\textsf{solve}$
function establishes that to prove any equality between two monoidal expressions, it suffices to prove that their normalised forms are equal. Yet—as we have seen previously—the monoidal equalities hold definitionally in our Cayley representation. As a result, the only ‘proof obligation’ we need to provide to the
$\textsf{solve}$
function establishes that to prove any equality between two monoidal expressions, it suffices to prove that their normalised forms are equal. Yet—as we have seen previously—the monoidal equalities hold definitionally in our Cayley representation. As a result, the only ‘proof obligation’ we need to provide to the
![]() $\textsf{solve}$
function will be trivial.
$\textsf{solve}$
function will be trivial.
Lets consider a simple example to drive home this point. Once we have established that lists are a monoid, we can use the
![]() $\textsf{solve}$
function to prove the following equality:
$\textsf{solve}$
function to prove the following equality:
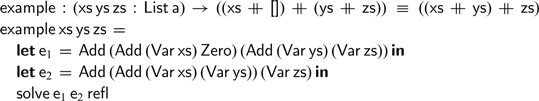
To complete the proof, we only needed to find monoidal expression representing the left- and right-hand sides of our equation—and this can be automated using Agda’s meta-programming features (Van Der Walt & Swierstra, Reference Van Der Walt and Swierstra2012). The only remaining proof obligation—that is, the third argument to the
![]() $\textsf{solve}$
function—is indeed trivial. In this style, we can automatically solve any equality that relies exclusively on the three defining properties of any monoid.
$\textsf{solve}$
function—is indeed trivial. In this style, we can automatically solve any equality that relies exclusively on the three defining properties of any monoid.
We can also show that natural numbers form a monoid under
![]() $\textsf{addAcc}$
and
$\textsf{addAcc}$
and
![]() $\textsf{Zero}$
. Using the associated solver, we can construct the proof obligations associated with the very first version of vector reverse from our introduction:
$\textsf{Zero}$
. Using the associated solver, we can construct the proof obligations associated with the very first version of vector reverse from our introduction:
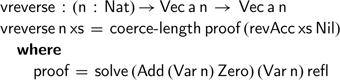
Even if the proof constructed here is a simple call to one of the monoidal identities, automating this proof lets us come full circle.
7 Discussion
I first learned of that monoidal identities hold definitionally for the Cayley representation of monoids from a message Alan Jeffrey (Reference Jeffrey2011) sent to the Agda mailing list. Since then, this construction has been used (implicitly) in several papers (McBride, Reference McBride2011; Jaber et al., Reference Jaber, Lewertowski, PÉdrot, Sozeau and Tabareau2016; Allais et al., Reference Allais, Chapman, McBride and McKinna2017) and developments (Kidney, Reference Kidney2020; Ko, Reference Ko2020)—but the works cited here are far from complete. The observation that the Cayley representation can be used to normalise monoidal expressions dates back at least to Beylin & Dybjer (Reference Beylin and Dybjer1995), although it is an instance of the more general technique of normalisation by evaluation (Berger & Schwichtenberg, Reference Berger and Schwichtenberg1991).
The two central examples from this paper, reversing vectors and constructing trees, share a common structure. Each function uses an accumulating parameter, indexed by a monoid, but relies on the monoid laws to type check. To avoid using explicit equalities, we use the Cayley representation of monoids in the index of the accumulating parameter. In the base case, this ensures that we can safely return the accumulating parameter; similarly, when calling the accumulating function with an initially empty argument, the Cayley representation ensures that the desired monoidal property holds by definition. In our second example, we also use the Cayley representation in the value of the accumulating parameter; we could also use this representation in the definition of
![]() $\textsf{vreverse}$
, but it does not make things any simpler. In general, this technique works provided we only rely on the monoidal properties. As soon as the type indices contain richer expressions, we will need to prove equalities and coerce explicitly—or better yet, find types and definitions that more closely follow the structure of the functions we intend to write.
$\textsf{vreverse}$
, but it does not make things any simpler. In general, this technique works provided we only rely on the monoidal properties. As soon as the type indices contain richer expressions, we will need to prove equalities and coerce explicitly—or better yet, find types and definitions that more closely follow the structure of the functions we intend to write.
Acknowledgements
I would like to thank Guillaume Allais, Joris Dral, Jeremy Gibbons, Donnacha Ois n Kidney and the anonymous reviewers for their insightful feedback.
Conflicts of Interest
None.
Supplementary materials
For supplementary material for this article, please visit https://doi.org/10.1017/S0956796822000065



Discussions
No Discussions have been published for this article.