Introduction
Early theoretical glaciology created two fundamentally different parabolic profiles as the shapes of steady flowline ice sheets lying on flat beds (Fig. 1). One was the profile of an ice sheet with perfect plasticity (E. Orowan comment in BGS, 1949; Reference NyeNye, 1952) and the other the profile for a sliding ‘plug’ flow (Reference BöðvarssonBöðvarsson, 1955). These global views of free surface flows in glaciology focus on different aspects of the problem and they come to rather different conclusions. Up to scaling, one is of the form x = 1 – z 2 (Orowan–Nye) and the other is of the form z = 1 – x 2 (Böðvarsson). The former perfect-plasticity solution has a central peak at the highest point of the ice sheet, and a margin with unbounded surface gradient. The latter plug-flow solution has a smooth dome and a finite-slope, wedge-shaped margin.

Fig. 1. The parabolas by Orowan (comment in BGS, 1949) and Reference NyeNye (1952) (dotted curve) and by Böðvarsson (1955; solid curve) for steady, flowline ice sheets on flat beds. A dome thickness of H 0 = 3000 m and a length of L 0 = 500 km are chosen for concreteness.
This paper shows how to combine Böðvarsson’s solution with a well-known exact solution for an ice shelf (Reference Van der VeenVan der Veen, 1983, Reference Van der Veen2013) to generate an exact solution for a flowline, steady marine ice sheet. It is shown in Figure 2. This exact solution simultaneously solves the steady mass-continuity equation and the so-called shallow-shelf approximation (SSA; Reference Weis, Greve and HutterWeis and others, 1999) stress balance. It is an exact solution in the rapidly sliding marine ice-sheet case (Reference SchoofSchoof, 2007), the model addressed by the MISMIP (Marine Ice-Sheet Model Intercomparison Project) intercomparison (Reference PattynPattyn and others, 2012). After presenting the model equations and constructing the exact solution in the next two sections, we examine the errors from two different numerical methods. We observe, through linearization of the equations around the exact solution, that the grounding line generates a strong ‘stiffness’ contrast, in the sense of numerical analysis.

Fig. 2. The geometry (solid curve) and velocity (dashed curve) of an exact solution of the simultaneous steady mass-continuity and SSA stress-balance equations for a marine ice sheet. The solution is Reference BöðvarssonBöðvarsson’s (1955) when grounded and Reference Van der VeenVan der Veen’s (1983, Reference Van der Veen2013) when floating.
Continuum Model
Model equations
Our model equations describe the steady-state, flat-bed case of the rapid-sliding model of Reference SchoofSchoof (2007, eqns (2.1–2.5)), but we restrict our consideration to the linear-sliding case. The primary unknowns in these equations are the ice thickness, H(x), velocity, u(x), and vertically integrated longitudinal stress, T(x) (Reference SchoofSchoof, 2006), where x is the flowline distance. Using the notation of Table 1, the equations are
Table 1. Notation and SI units or values. Values of physical constants

Here the subscript x denotes the derivative. Equations (1) and (2) are the mass-continuity and SSA stress-balance equations, respectively, while Eqn (3) defines T. In Eqn (1) the climatic-basal mass-balance rate, M(x) (Reference CogleyCogley and others, 2011), also called the accumulation/ablation rate function, combines the surface mass-balance rate and the rate of basal melt/refreeze. In grounded ice the basal shear stress is linear, so τ b = -βu (Reference MacAyealMacAyeal, 1989) appears in Eqn (2), with β = 0 in floating ice, so the same linear form holds throughout. The coefficient B(x) in Eqn (3) is called the ice ‘hardness’.
Let ω = 1 – ρ/ρw be the ‘Archimedean factor’, which relates ice surface elevation to thickness in floating ice. Let z o be the elevation of the ocean surface. The grounded ice rests on bedrock at elevation b, which is a constant in this paper. By the flotation criterion,
defines the ice surface elevation in grounded and floating cases, respectively. Using the same flotation criterion we can clarify the basal shear stress,
where we have scaled β = kρgH with the ice overburden pressure, ρgH, following Reference BöðvarssonBöðvarsson (1955).
Equations (1–5) apply on an interval 0 < x < x c, where x c is the floating calving front. We must solve for the location, x = x g, of the grounding line, at which we know ρH (x g) = ρ w(z o – b).
For the exact and numerical solutions in this paper, Eqns (1–5) are augmented by boundary conditions:
where ua and Ha simply denote Dirichlet boundary values for velocity and thickness respectively. Here x = 0 is an upstream location where Dirichlet boundary conditions are applied (Eqn (6)), while at the calving front, x = x c, we have the standard hydrostatic pressure imbalance condition, Eqn (7) (Reference SchoofSchoof, 2007).
On well-posedness and the grounding line
Given data B (x), b, k > 0, M (x), x c > 0, z o, along with physical constants g, n, ρ, ρ w, we expect the problem consisting of Eqns (1–8) to be well-posed. To our knowledge this has not been proved, nor do we attempt to prove it. It is, however, now worth considering the smoothness of the solution to Eqns (1–7), including what hypotheses would lead to satisfying Eqn (8) at the free (i.e. unknown) location x g in the interior of the domain.
Suppose that, for physical reasons, the climatic-basal mass-balance rate, M (x), and ice hardness, B (x), are bounded, and further that B (x) is bounded below by a positive constant. On integrating M, Eqn (1) implies that the flux, q = uH, is absolutely continuous and bounded. If there is a positive lower bound on thickness, H, then we can conclude that the magnitude of u is bounded because u = q/H. If the magnitude of the driving stress, -ρgHhx , is bounded then Eqn (2) implies T is absolutely continuous. By Eqn (3) this implies u has a bounded and integrable derivative, and, thus, that u is also absolutely continuous. From these facts we could then return to the flux and write H = q/u, which shows H is absolutely continuous away from locations where u = 0 (e.g. divides). In summary, assuming (i) that an integrable solution (H, u, T) to Eqns (1–7) exists, (ii) that the functions M, B are bounded and integrable, (iii) that B is bounded below by a positive constant, (iv) that a positive lower bound on thickness exists and (v) that an upper bound on the magnitude of the driving stress exists, then we can regard the conditions of Eqn (8), giving continuity at the grounding line, as properties of the solution instead of as part of the ‘imposed’ problem statement. Thus, from now on we speak of solving the problem consisting of Eqns (1–7), with the location of the grounding line, x g, unknown, and with Eqn (8) describing proportion of the solution.
Exact Solution
Böðvarsson’s parabola
Reference BöðvarssonBöðvarsson (1955) built, based on minimal existing literature, a rigorous theory of the flow of glaciers and ice sheets. His test case was Brúarjökull, a glacier on the northern margin of Vatnajökull, Iceland. It flows over a smooth bed for 20 km, from a location where its thickness is 600 m, to a zero thickness margin. This glacier is entirely grounded. He showed that a good fit to measured surface elevations can be made using his model.
He initially states an equation for the ice-sheet surface elevation which has both vertical-plane shear and longitudinal stresses within the ice. However, he says this equation ‘is quite tedious and very difficult to handle especially because of the [shear term]. It is therefore fortunate that [the shear] term appears to be small compared to the [basal sliding] term.’ Then he drops the shear term and writes an equation in which driving stress is balanced by sliding resistance. He solves and analyzes this plug-flow model, for which we now state his equations in detail.
As is perhaps best known about Böðvarsson’s work, he chooses the surface mass-balance rate to be
for a mass-balance gradient a > 0 and equilibrium-line altitude H ela. Böðvarsson’s basal resistance formula scales with the overburden pressure, so that the basal shear stress is
He then writes the ice flux as uH = – (H/k)Hx , or equivalently the ice velocity as
(We return to Eqn (11) below, explaining it in modern language.) Combining Eqns (9) and (11) with mass continuity (Eqn (1)) yields Eqn (17) of Reference BöðvarssonBöðvarsson (1955), namely
His thickness solution to this equation is (Reference BöðvarssonBöðvarsson, 1955, Eqns (18) and (23))
where H 0 = 1: 5H ela and akL 2 0 = 9H ela (Reference BöðvarssonBöðvarsson, 1955, Eqn (24)).
Despite its simplicity, Eqn (13) is an exact solution to Eqn (12), with boundary condition H (0) = H 0, as the reader may verify. The formula of Eqn (13) defines the solid parabola shown in Figure 1. Böðvarsson does not offer a reason why there should be such a simple quadratic solution to Eqn (12). His solution seems to be a new result for a narrow class of nonlinear second-order ordinary differential equations (ODEs) like Eqn (12) (Appendix A). Seeking a polynomial solution to Eqn (12) with the single boundary condition H (0) = H 0, as in Appendix A, generates a location, x = L 0, where both the flux and the thickness are zero. Böðvarsson explicitly considers the solution, Eqn (13), as solving a free-boundary problem in this sense.
Böðvarsson had a particular ‘sliding law’ in mind, namely Eqn (10), in which the sliding coefficient scales with overburden pressure. The modern reader may protest that β should instead be a function of (e.g. proportional to) effective pressure, N = ρgH – P, where P is the subglacial water pressure. However, it is not unreasonable to suppose that P also scales with (is roughly a fixed fraction, λ, of) overburden pressure. In that case we have equations β = cN, N = ρgH – P and P = λρgH, which combine to give β = c(1 – λ)ρgH. Thus, if the reader so wishes, in Böðvarsson’s model we can write β = kρgH with k = c(1 – λ).
Reference BöðvarssonBöðvarsson’s 1955 paper was apparently first cited by Reference WeertmanWeertman (1961), who decided that his sliding, plug-flow physics should be replaced by a shear deformation model more like the shallow-ice approximation. This replacement seems to have influenced readers from then on. The surface balance parameterization, Eqn (9), also reappears in Reference WeertmanWeertman (1961), among other places. It parameterizes a potential climatic instability, which was Böðvarsson’s, Weertman’s and most readers’, major interest. We are, however, interested now in Böðvarsson’s solution to the ice-flow equations themselves.
An SSA re-interpretation
We have claimed that Eqn (13) exactly solves a combination of the steady flowline mass-continuity equation (Eqn (1)) and the SSA stress-balance equation (Eqn (2)), but the source of Eqn (11) may be less clear. However, suppose we look for solutions of Eqns (1) and (2), with constant vertically integrated longitudinal stress, Tx = 0. In that case Eqn (2) and the scaling, Eqn (10), implies Böðvarsson’s formula for the velocity, namely Eqn (11). Furthermore, Eqns (1) and (9) then give Böðvarsson’s main equation, Eqn (12). That is, if (i) Tx = 0, (ii) sliding resistance is linear and scales with overburden pressure and (iii) climatic-basal mass-balance rate is proportional to elevation above the equilibrium line, then we can recover a simple parabolic profile for H (x), namely Eqn (13), which is a solution to Eqn (12).
But what does the condition Tx = 0 imply as a relation among the modeled quantities? Given a thickness profile H (x) and a strain-rate profile ux (x), we may interpret Tx = 0 as a statement of variable ice hardness, B (x). Generally, variation in hardness can be physically explained (e.g. in numerical models that use the SSA in a temperature-dependent way (Reference Bueler and BrownBueler and Brown, 2009)), so assuming that hardness is x –dependent requires no conceptual extensions in the marine ice-sheet modeling context. Numerical models can therefore use the exact solution we are building for verification without requiring unusual modifications.
Thus the variable hardness, B (x), used here allows us to ‘manufacture’ an exact solution (Reference Bueler, Lingle, Brown, Covey and BowmanBueler and others, 2005). Specifically, the assumption T = T 0 in Eqn (3) yields a formula for ice hardness in grounded ice:
The value T 0 in Eqn (14) will be set by a downstream stress condition, just as it is in many models for flowline ice shelves (e.g. Reference SchoofSchoof, 2007; Reference PattynPattyn and others, 2012).
Extending the exact solution to floating ice
Two well-known observations are relevant to the argument in the next paragraphs: (i) For floating ice with β = 0, Eqns (1–7) also have a known exact solution, specifically in the case where the climatic-basal mass-balance rate, M, and the ice hardness, B, are constant (Reference Van der VeenVan der Veen, 1983, Reference Van der Veen2013); (ii) The vertically integrated longitudinal stress, T, in a flowline ice shelf (i.e. one without lateral stresses) satisfies Eqn (7) at each location, x, in the shelf, i.e. T (x) = ½ ωρgH(x)2, because this is a first integral of Eqn (2) if β = 0.
Based on these observations we can construct a marine ice-sheet exact solution by connecting Böðvarsson’s grounded solution to floating ice. Note the grounding-line thickness is H (x g) = (ρ w /ρ)z o if we take b = 0. Then from Böðvarsson’s thickness solution (Eqn (13)) we can determine x g. At x g, from Eqns (11) and (13), we also know u (x g). For x g ≤ x ≤ x c, the floating ice shelf, we then set M (x) = M (x g) as constant from Eqn (9), thus making M (x) continuous across the grounding line, while at the same time allowing us to use Van der Veen’s construction, which is based on a constant climatic-basal mass-balance rate. The equation T (x) = ½ ωρgH (x)2 determines T 0 = T (x g) for use in Eqn (14), which determines B (x g) in particular, and so we then set B (x) = B (x g) for x g ≤ x ≤ x c, a constant, also needed in Van der Veen’s construction.
The results of the above choices are the following formulas for an exact marine ice sheet satisfying our steady model equations (Eqns (1–8)). The velocity combines the Reference BöðvarssonBöðvarsson (1955) and Reference Van der VeenVan der Veen (1983) results,

where the shelf velocity u s(x) is defined by
Cs = [ρgω/4B(xg))]n, Q g = u (x g)H (x g) and Q s(x) = Q g + M (x g)(x – x g). Similarly the thickness isM

Equations (15) and (17) define the continuous functions shown in Figure 2, using the specific values given in Table 2.
Table 2. Specific values used in (above divider) or determined by (below divider) the equations that define the exact solution shown in Figures 2–5. Note ‘g.l.’ = grounding line and ‘c.f.’ = calving front

As described above, from the thickness, H (x), and the velocity, u (x), we can find continuous functions, M (x) and B (x), for the full flowline, using Eqns (9) and (14). These functions are shown in Figure 3. Then we can use Eqn (3) to find T (x); this is shown in Figure 4. In Figure 4 we also show the sliding coefficient, β (x), which drops to zero discontinuously at x g. Finally Figure 5 shows a detail of the grounding line and floating ice in the exact solution.

Fig. 3. The climatic-basal mass-balance rate, M (x) (solid curve), and ice hardness, B (x) (dashed curve), for the exact solution.

Fig. 4. The sliding coefficient, β (x) (solid curve), and the vertically integrated longitudinal stress, T (x) (dashed curve), for the exact solution. The solid curve shows β = kρgH on both sides of the grounding line. The actual basal resistance experienced by the shelf drops to zero at the grounding line (dotted line).
The floating ice shelf is a relatively short 40 km (Figs 2 and 5). To explain, note that the equilibrium-line altitude, H ela, in Reference BöðvarssonBöðvarsson’s (1955) solution is high on the ice sheet because of its relation to the upstream ice thickness in the construction of the exact solution (i.e. H ela = (2/ 3)H 0). This, in turn, implies M (x g) is quite negative (Eqn (9); Fig. 3). Because Reference Van der VeenVan der Veen’s (1983) solution uses a constant climatic-basal mass-balance rate, and because we want continuity for M (x), we therefore have an ice shelf experiencing rapid melting. The location of the calving front, x c, must, of course, be put upstream of the location where the ice has melted away. As a result of these same factors we also see a rapid decline in the stress, T (x), from its constant grounded value to its small value at x c (Fig. 4; Table 2). Though the ice shelf shown here is very wedge-like, the thickness, H (x), for floating ice comes from Eqn (17), and it is not a linear function because u s(x) is not constant on the shelf.

Fig. 5. Detail of Figure 2, showing the floating ice-shelf geometry and velocity.
Numerical Results
Verification of a grid-free ‘shooting’ numerical method
In our steady flowline case the model equations form a two-point boundary-value problem (BVP) for ODEs. Specifically, the three first-order ODEs, Eqns (1–3), are subject to two boundary conditions: Eqn (6) at x = 0 and the calving-front stress condition, Eqn (7), at x = x c.
A nonlinear ‘shooting’ method (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992, section 17.1) applies to this problem. We use the correct values for u (0) and H (0) from Eqn (6) and guess an additional value, T 0, for T (0). Then we use a numerical ODE initial-value problem (IVP) solver to compute a solution, (ũ(x), (x), (x)), from x = 0 to x = x c. The failure of this ODE IVP solution to satisfy boundary condition Eqn (7) is a measure of the wrongness of T 0. In fact, based on Eqn (7) we define the function
and then we can apply a numerical method to find the solution (root),0, to the problem F (T 0) = 0. This root gives us complete initial conditions, so that the ODE IVP solution also solves the two-point BVP, Eqns (1–7).
A robust root-finding method is bisection (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992, section 9.1). It is guaranteed to converge if F is continuous and if an initial bracket is given, which is easy to find in this case. Regarding faster root-finding methods than bisection, such as Newton’s method, we observe that F ’ may not exist because of the low regularity of the solution at the interior point, x = x g. However, by using our exact solution we will see clear evidence that the bisection iteration succeeds in finding the root,0, to many digits, despite the uncertain smoothness of F.
This ‘shooting’ method has the advantage that the advanced step-size control mechanism of an ODE IVP solver determines the spatial gridpoints, so as to solve the ODEs to a desired tolerance. Thereby we avoid an a priori choice of the grid, and in this sense the method is grid-free. In this case we use LSODA from the ODEPACK collection (Reference Hindmarsh, Stepleman, Carver, Peskin, Ames and VichnevetskyHindmarsh, 1983), because it both automatically adjusts step-size to achieve desired tolerance and automatically switches method when stiffness (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992, section 16.6) is detected.
We now apply this grid-free procedure to the same problem for which we have the exact solution (given in Eqns (15–17)). Using relative tolerance 10-12 and absolute tolerance 10-14 for LSODA we get the numerical error shown in Figure 6. We have shown the error in two runs, one in which we have used the exactly correct initial value, T 0, (‘cheating’) and one in which we start with a large initial bracket on T 0 and converge on the correct calving-front boundary condition through shooting and bisection (‘realistic’). In the ‘cheating’ runs we see that the numerical error just from solving the ODE, i.e. independent of errors in boundary conditions, is quite small, in the 10th or 11th digit for H and u. The much larger error seen in the ‘realistic’ case suggests, however, that F in Eqn (18) is significantly irregular. Apparently, matching the calving-front boundary condition by numerical shooting from upstream causes the loss of 4 or 5 digits of accuracy. Nonetheless, even in this ‘realistic’ case our numerical method achieves 6- or 7-digit accuracy over the whole domain, including in the immediate vicinity of the grounding line. Note that though the peak thickness error is near the grounding line, it is only modestly larger than errors elsewhere.

Fig. 6. Pointwise error in thickness (upper panel) and in velocity (lower panel) from an adaptive numerical ODE scheme. Both the ‘cheating’ case (solid curve), where we use the exactly correct initial value for T, and the ‘realistic’ case (dashed curve), where the shooting method converges on the correct initial value for T by the bisection method, are shown.
The ODE solver also detects the grounding line as a point of transition to shorter (spatial) steps, as seen in Figure 7. More significantly, however, the grounded ice requires a stiff method while the floating ice allows a non-stiff one, according to the automatic switch mechanism in LSODA. Note that high accuracy (e.g. 6 or 7 digits) is achieved in the ‘realistic’ case, despite rather large grid spacing in the grounded ice, with large portions at 5–10 km spacing. The spacing drops to a minimum of 100 m just downstream of the grounding line at x g = 350 km.

Fig. 7. The adaptive numerical ODE scheme in the ‘realistic’ case makes steps of 1–10 km in grounded ice, but at the grounding line, x g = 350 km, the step size is reduced to a few hundred meters. The adaptive mechanism automatically switches from a stiff method where grounded (circles), to a non-stiff method where floating (stars).
In all numerical tests we have treated M (x) as a predetermined field (i.e. the one shown in Fig. 3). This removes the climatically important elevation–accumulation feedback, and the associated instability, of interest to Reference BöðvarssonBöðvarsson (1955) and others. This feedback can, however, be restored by using Eqn (9) to determine M from H.
Linearization around the exact solution
The above numerical evidence shows that a distinct change in stiffness occurs at the grounding line. To analyze this we linearize the model equations around the exact solution. Denote the exact solution (0,0,0) and consider a small perturbation u = + εũ, H = + ε and T = + ε. Denote the column vector of perturbations by w = [ũ,, ]T Assuming x > 0, Eqns (1–3) imply that, to first order in ε, the perturbation solves this linear ODE system in grounded ice:

where p = 1/n – 1. In floating ice, only the last rows differ from Eqn (19):
If we define L (x) and R (x) to be the left- and right-side matrices in Eqns (19) and (20) then w solves
along its whole length, where A (x) = L (x)-1 R (x).
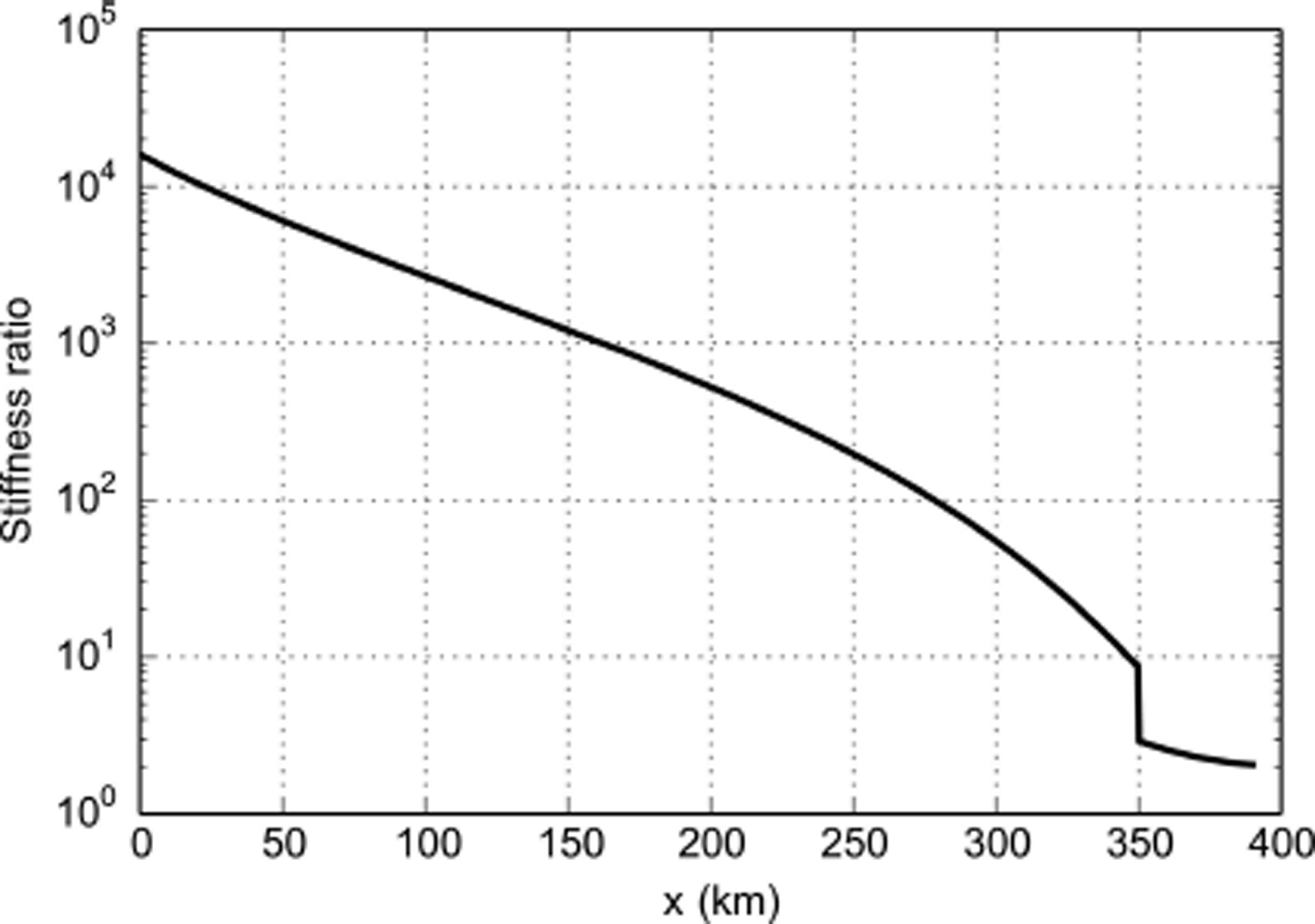
Linear ODE system Eqn (21) is stiff if there is a large ratio of magnitudes in the eigenvalues of A (x) (Reference Press, Teukolsky, Vetterling and FlanneryPress and others, 1992). Because the entries and eigenvalues of A (x) are exactly computable using the exact solution values, ((x), (x), (x)), we can plot (Fig. 8) the x –dependent ‘stiffness ratio’ for A (x), namely the ratio of absolute values of the real parts of the largest and smallest eigenvalues of A (x), along the whole length of the flowline. Note this ratio is small in the non-stiff floating ice. This ratio is independent of the direction of integration (i.e. upstream versus downstream). The stiffness ratio is by no means the last word on quantifying stiffness, which turns out to be difficult generally (e.g. Reference Higham and TrefethenHigham and Trefethen, 1993).
We believe that the strong stiffness contrast at the grounding line is significant in explaining large near-grounding-line errors made by gridded numerical methods (Reference Gladstone, Payne and CornfordGladstone and others, 2010; Reference PattynPattyn and others, 2012). The stiffness ratio drops by a factor of almost ten at the grounding line, though it is largest in the interior part of the grounded ice. It is possible that models of modified effective pressure near the grounding line (Reference Leguy, Davis and LipscombLeguy and others, 2014), in sliding laws that are parameterized by effective pressure (Reference SchoofSchoof, 2005), can smooth this stiffness contrast.
Verification of a fixed-grid finite-difference numerical method
We also implemented an equally spaced, second-order, finite-difference scheme using Newton iteration (Appendix B). Our exact solution allows us to measure, for the first time in a rapidly sliding marine ice-sheet context, the errors from such a numerical scheme of the common type implemented in practical marine ice-sheet models (e.g. Reference Pollard and DeContoPollard and DeConto, 2009; Reference WinkelmannWinkelmann and others, 2011).
It is important to distinguish the errors attributable to the finite-difference discretization itself from errors attributable to imperfect convergence of the nonlinear iterative solver that is applied to solve the discretized equations. To evaluate the former type of errors we initialized the nonlinear solver with the exact solution values. These are not the exact solutions of the discretized equations but they are (obviously) close. We see converged solutions to the discretized equations down to 5 m grids. The resulting thickness and velocity errors, at the mm and mm a–1 level, respectively (Fig. 9), are larger than from the adaptive (grid-free) higher-order ODE method above (cf. Fig. 6). Nonetheless errors at this level are certainly acceptable, if they were to represent the realistic case.
Figure 9 shows that the maximum numerical thickness and velocity errors are observed to converge at a rate much slower than the optimal O(Δx 2) rate under grid refinement (Reference Morton and MayersMorton and Mayers, 2005). This is essentially because of the loss of smoothness in the exact solution at the grounding line. By contrast, use of the grounded-only Reference BöðvarssonBöðvarsson (1955) exact solution, without a grounding line, confirms that the same finite-difference method gives optimal O(Δx 2) convergence (not shown).

Fig. 9. Maximum errors in ice thickness (upper panel) and velocity (lower panel) on grids with spacing from 20 km to 5 m. When initialized with the exact solution, the numerical scheme converges at a rate Δx 1.08 for both thickness and velocity (large dots plus dotted line). For a more realistic initial iterate the convergence rate is initially good, but at resolutions <1 km the Newton iteration fails to converge (stars).
However, if we use a simple ‘wedge’ initial iterate, which has a linear thickness profile from the upstream initial condition, H (0), down to 300 m at the calving front, and a similar linear velocity profile increasing from u (0) to 300 m a-1 at the calving front, then we see more realistic results, that reflect the experience of ice-sheet modelers addressing these equations. Here the initial iterate is relatively far from the exact solution. Difficulties arise in the global convergence behavior of the Newton solver, even though standard line-search techniques are used in these computations (Reference KelleyKelley, 1987). For grids finer than 1 km the iteration for this scheme does not converge, apparently because the Jacobian matrix is not providing useful directional information as to the location of the solution of the discretized equations.
Our results suggest a lack of nonlinear solver robustness that we attribute to the non-smooth, stiffness-contrasting properties of the problem near the grounding line. Grounding-line parameterizations (e.g. Reference Gladstone, Payne and CornfordGladstone and others, 2010; Reference Feldmann, Albrecht, Khroulev, Pattyn and LevermannFeldmann and others, 2014) may act like homotopy continuation methods (Reference KelleyKelley, 1987) to improve global solver behavior in this case, but such considerations go beyond the scope of this paper. No regularization of grounding-line discontinuities and slope discontinuities in the formulas for β (x) and h (x) (respectively) were applied in this paper.
Conclusion
As noted by Reference Bueler, Lingle, Brown, Covey and BowmanBueler and others (2005), Reference WesselingWesseling (2001) and many others, verification of numerical methods is a valuable first step in effective numerical modeling of realistic flows. This is especially so in geophysical flows, where validation by comparison with controlled laboratory experiments is difficult. Thus, the rediscovery of an exact solution to a marine ice-sheet problem is a welcome development. Even though this solution is for a steady-state and flat-bed case, it provides a partial alternative to using hard-to-interpret inter-comparison results (Reference PattynPattyn and others, 2012).
Because this solution is found in some of the first work in theoretical glaciology (Reference BöðvarssonBöðvarsson, 1955), we have recovered an early approach to sliding dynamics. The rapid-sliding case turns out to be one of the first dynamical situations examined, even though other early efforts at global views of ice dynamics tended toward the plastic-ice (Orowan comment in BGS, 1949; Reference NyeNye, 1952), frozen-bed (Reference VialovVialov, 1958) and vertical-shear dominated (Reference WeertmanWeertman, 1961) models, and these came to dominate the field until recent decades.
Citations of Reference BöðvarssonBöðvarsson (1955) usually relate to its theory of climatic instability for glaciers and ice sheets, in which surface mass-balance rate depends on elevation. The only citation exception to this pattern known to the current author is that Reference BöðvarssonFowler (1992) refers to the basal-shear-dominated dynamics of Reference BöðvarssonBöðvarsson (1955) as ‘approximate results’. We hope that the current work revives interest in Böðvarsson’s ice-dynamical solution and corrects the misreading of his results as approximate.
Application of the new exact solution here, which includes a floating extension, also reveals one feature of the marine ice-sheet problem that we feel has been overlooked, namely that there is a strong stiffness contrast at the grounding line, in the sense of differential equations. This is, conceptually, in addition to the loss of smoothness seen at the grounding line. Both smoothness and stiffness must be addressed by numerical methods. Modelers should have more than grid refinement in mind as they attempt to model grounding lines correctly.
Acknowledgements (and Erratum)
Comments from referees R. Gladstone and K. Hutter have focused and improved the paper. Thanks to G. Aðalgeirsdóttir, H. Blatter and H. Björnsson for tracking down a copy of Reference BöðvarssonBöðvarsson (1955) and a bibliography of the works of Gunnar Böðvarsson. Reference Bueler, Lingle, Brown, Covey and BowmanBueler and others (2005) incorrectly identify the constant accumulation SIA solution as ‘Reference BöðvarssonBöðvarsson (1955)–Vialov (1958)’. In fact it is attributable only to Vialov. Finally, note that spellings of Böðvarsson include ‘Böðvarsson’ (e.g. in Reference BöðvarssonBöðvarsson, 1955) and ‘Böðvarsson’ in the literature.
Appendix A: Böðvarsson’s Little Theorem
Böðvarsson (1955) does not identify a source for the exact parabolic thickness solution to his flow equations, and we have not been able to attribute it to earlier work. We summarize his result as the theorem that there is a unique polynomial solution, y (x), to the nonlinear second-order differential equation
satisfying the single boundary condition, y (0) = y 0 > 0, subject to both an initial downslope assumption (y ’(0) ≤ 0) and to the technical inequality 2c 1 y 0 + 3c 0 ≥ 0.
Equation (A1) is Eqn (17) of Böðvarsson (1955). The additional assumptions (i.e. initial downslope plus the technical inequality) are unstated, though he comments that there is ‘one and only one solution which is admittable from the physical point of view’.
Here we justify this little theorem and, generally following Böðvarsson (1955), derive relations among parameters which allow a solution. The unique polynomial solution may be interpreted as solving a free-boundary problem for the first positive zero x 0 > 0 of y (x). In Böðvarsson’s context x 0 = L 0 is the length of the glacier, the location of the margin in the everywhere-grounded case.
It is easy to see by substitution into Eqn (A1) that nontrivial solutions of degree d, i.e. of the form y (x) = Cxd + (lower degree) with C ≠ 0, exist only if d = 2. In that case we seek solutions that satisfy the boundary conditions y (0) = y 0 and y ’(0) ≤ 0, so
for some α ≥ 0 and γ, which are to be determined (this is Eqn (18) of Böðvarsson, 1955). Substitution of Eqn (A2) into Eqn (A1) gives the two equations
These two relations determine α and γ from c 0 and c 1. The first relation explains the technical inequality, noting 3y 2 0 α 2 ≥ 0, of course.
In his main text, Böðvarsson (1955) relates four numbers to the unknown glacier thickness, which is y (x) in the above formulas: the initial (upstream) ice thickness, H 0, an ablation gradient, a > 0, the equilibrium-line altitude, H ela, and a scaled sliding coefficient, k > 0. He has c 0 = kaH ela and c 1 = –ka in Eqn (A1), so the technical inequality says 3H ela ≥ 2H 0 after simplification. This causes the equilibrium-line altitude to be relatively high on the glacier.
Appendix B: A Finite-Difference Scheme
The steady-state equations for mass continuity (Eqn (1)) and stress balance (Eqn (2)) form a coupled system that can be approximately solved by the centered, second-order finite-difference scheme described here. There is no claim that this scheme is optimal, but merely that it is a reasonable fixed-grid method for initial evaluation. Because we use it to solve a steady-state problem, it generalizes to the time-dependent case as an implicit method.
We define an equally spaced grid on the domain [0, x
c]. Because the boundary condition at the calving front evaluates the stress, T, we put the right endpoint, x
c, at a ‘staggered’ location halfway between gridpoints. Thus if N is the number of spaces we define Δx = x
c
= (N + 1/ 2) and xj
= j Δx for j = 0,…, N + 1. Denote the numerical approximations Hi
≈ H (xi
) and ui
≈ u (xi
). Let ![]() be the staggered location for j = 0,…, N. Note
be the staggered location for j = 0,…, N. Note ![]() . Denote
. Denote ![]() .
.
The mass-continuity equation (Eqn (1)) is approximated by a second-order difference centered at the staggered location. For j = 0,…, N,
In Eqn (2) we avoid infinite viscosity by using a regularization (Schoof, 2006). Let ε = 1/x c per year, i.e. a strain rate corresponding to 1 m a-1 velocity change over the whole domain. Define
where u l and u r are velocity values to the left and right of a staggered gridpoint, respectively. Then we approximate the stress, T, at staggered points,
For j = 0,…,N. Equation (2) is approximately
for j = 1,…, N, where βj = kρgHj if the ice is grounded at xj (i.e. if ρHj ≥ ρ w(z o – b)) and βj = 0 if the ice is floating, and where hj = Hj + b if the ice is grounded and hj = ωHj + z o if the ice is floating. Thus Eqn (B4) applies, as stated, both for grounded and floating ice. At this point we have 2N + 4 scalar unknowns, namely uj and Hj for j = 0,…, N + 1. There are 2N + 1 nonlinear equations in Eqns (B1) and (B4). The two upstream Dirichlet equations (Eqn (6)), namely u 0 = u (0) and H 0 = H (0), bring the number of equations to 2N + 3. The following approximation of the calving-front condition (Eqn (7)), completes the system:
where T * N is the approximation given in Eqn (B3).
Thus we have a system of 2N + 4 nonlinear equations in the same number of unknowns. One can write this system abstractly as F(v) = 0. These equations are solved by Newton’s method (Reference KelleyKelley, 1987), as implemented in the PETSc library (Reference BalayBalay and others, 2014). A residual evaluation function computes F(v) given v. A finite-difference Jacobian matrix, J = F ’, can then be computed by PETSc, and this allows us to solve systems up to size N ≈ 103. We also implemented an exact Jacobian using by-hand differentiation of the above formulas. For initial guesses sufficiently near the exact solution, this exact Jacobian permits solutions of the system for up to N = 105. A full analysis of the robustness and convergence rate of this Newton solver is beyond the scope of the current paper.