Introduction
Modeling the flow of ice is central to glaciology. A glacier model can be used to predict changes in response to climate change (e.g. Reference Oerlemans and van der VeenOerlemans and Van der Veen, 1984). Inversely, observed changes of glaciers and ice sheets are related to the climate history, but the dynamics of glacier flow makes this relationship complex. Accurate glacier models are also important to help date and interpret ice cores (e.g. Reference Dahl-JensenDahl-Jensen, 1989) or to assess glacier-related natural hazards (e.g. Reference Pralong, Funk and LuthiPralong and others, 2003).
A temperate glacier can be modeled by considering the equations of mass and momentum balance, a flow law and boundary conditions (e.g. Reference HutterHutter, 1983). The surface boundary condition is that of a stress-free surface and a prescribed climate (accumulation/ablation). The bottom boundary condition consists of a melting rate defining the velocity component perpendicular to the bed, and a sliding law defining the basal velocity, often as a function of the basal shear stress and/or basal water pressure (e.g. Reference Budd, Keage and BlundyBudd and others, 1979).
Formulating a glacier flow model poses many challenges, but one of the most fundamental is a poor understanding of the basal boundary condition. This is a significant problem, because basal motion can be 50% or more of the total glacier or ice-stream motion. Direct measurements of basal motion are often difficult or impossible to obtain, for obvious reasons. Theoretical sliding laws for ice overlying bedrock have been derived (Reference LliboutryLliboutry, 1968; Reference KambKamb, 1970; Reference NyeNye, 1970; Reference IkenIken, 1981; Fowler, 1986; Reference Truffer and IkenTruffer and Iken, 1998), but they do not perform well on a macroscopic scale (e.g. Reference Iken and TrufferIken and Truffer, 1997). Some observations indicate that water storage plays an important role for basal motion (Reference Kamb, Engelhardt, Fahnestock, Humphrey, Meier and StoneKamb and others, 1994; Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2001), but no useful parameterization of this relationship has yet been proposed. An added complication is that many glaciers rest on sediments. Viscous models of sediment deformation lead to basal boundary conditions similar to the ones mentioned above (Reference Boulton and HindmarshBoulton and Hindmarsh, 1987), but laboratory experiments show a strongly non-linear or even plastic behavior (e.g. Reference KambKamb, 1991), which motivated Truffer and others (2001b) to introduce a stress boundary condition into their flow model. Usually it is not even possible to infer the subglacial morphology (hard vs soft vs mixed beds), but, even if that was known, there are no appropriate general boundary conditions.
Contrary to the situation at the bottom of a glacier, measurements on the glacier surface are much easier to accomplish, either by field or remote-sensing methods. In particular, synthetic aperture radar (Reference Goldstein, Engelhardt, Kamb and FrolichGoldstein and others, 1993) has made it possible to measure the surface velocity fields of glaciers (Reference Fatland and LingleFatland and Lingle, 1998; Reference Michel and RignotMichel and Rignot, 1999) and large parts of the ice sheets (Reference Fahnestock, Bindschadler, Kwok and JezekFahnestock and others, 1993; Reference Joughin, Kwok and FahnestockJoughin and others, 1996, 1999, 2000; Reference Rignot, Gogineni, Krabill and EkholmRignot and others, 1997, 2001; Reference Mohr, Reeh and MadsenMohr and others, 1998). Airborne and ground geophysics also provide an increasing dataset of ice thickness and surface topography (Reference Bamber, Ekholm and KrabillBamber and others, 2001a, Reference Bamber, Layberry and Goginenib; Gogenini and others, 2001; Reference Lythe and VaughanLythe and others, 2001; Reference Arendt, Echelmeyer, Harrison, LingleandV and ValentineArendt and others, 2002).
Mathematically, this sets up a classic ill-posed problem: it can be shown that infinitely many assumptions for the basal velocity field lead to the same surface velocities. Essentially, there are too many boundary conditions at the top and not enough at the bottom. This situation is common in many other areas of science, particularly geophysics. It is typically addressed by inverse methods.
Inverse theory is becoming an increasingly popular tool in glaciology. Reference Van der Veen and WhillansVan der Veen and Whillans (1989) pioneered the force budget method. It uses geometry and surface velocities as input and calculates basal velocities by solving the momentum equations in successive layers from the top down. This method is numerically unstable, however, and it magnifies input errors (Reference Bahr, Pfeffer and MeierBahr and others, 1994; Reference LliboutryLliboutry, 1995). It lacks the capability to deal with errors in the input data, and it provides no mechanism to choose a desirable solution among the infinitely many possible solutions. On the other hand, the force budget method works well for estimating basal shear stresses on the scale of several ice thicknesses.
Reference MacAyealMacAyeal (1993) applied control theory to calculate the basal friction of Ice Stream E, West Antarctica. He solves a well-posed forward model assuming some basal friction. The friction is then used as an adjustable parameter to minimize a misfit functional (calculated vs observed surface velocities) using an adjoint trajectory method. This theory is robust and has also been successfully applied to West Ant- arctica’sWhillans Ice Stream (Reference Rommelaere and MacAyealRommelaere and MacAyeal, 1997) and the northeast Greenland ice stream (Reference Joughin, Fahnestock, MacAyeal, Bamber and GogineniJoughin and others, 2001), where a finite-element forward model (Reference MacAyealMacAyeal, 1989; Reference Hulbe and MacAyealHulbe and MacAyeal, 1999) was inverted. Reference Gudmundsson, Raymond and BindschadlerGudmundsson and others (1998) chose an analytical approach and calculated transfer functions for basal velocities and topography, and inverted those.
Here we propose to use a different approach, based on inverse methods common in geophysics and many other areas (Reference MenkeMenke, 1989; Reference ParkerParker, 1994).
Methods
In this paper we will adapt textbook inverse methods to an analytical one-dimensional glaciological model developed by Reference Kamb and EchelmeyerKamb and Echelmeyer (1986). It is particularly simple, because it can be linearized. We will follow an approach outlined by Parker (1994, section 3).
The first step in inverse modeling is the formulation of a forward model. A forward model is a well-posed problem; in our case it is a model to calculate surface velocities, given an appropriate basal boundary condition (such as basal velocities). In general terms, a linear forward model can be written as an inner product:
where dj are N numbers that can be derived from measurements taken at discrete points, xj . The so-called model m is a continuous function of the longitudinal coordinate x and gj are continuous functions of xj – x, called representers. Equation (1) defines a linear forward model. If m is known, dj can be calculated. The inverse model finds m given dj . If we treat m as a function in a Hilbert space V, and dj are N real numbers, then the inverse problem is underdetermined and infinitely many exact solutions exist for m. The goal then is to find a measure of m to optimize, so the best solution in some sense can be selected. We will choose a norm (actually a semi-norm) based on the first derivative. This procedure will select for a smooth solution, i.e. one with a small first derivative. Even though the data can be fitted exactly, it is advantageous to relax this criterion. The data will only be fitted within a given tolerance.
As an example we will present a one-dimensional forward model that can be linearized. It treats the flow of glacier ice down an inclined channel. An analytical solution exists for the surface velocity of an inclined slab (inclination α, thickness h) of infinite extent (Reference PatersonPaterson, 1994):

where u plate is the surface speed. Equation (2) is derived by treating ice as a non-linear viscous fluid: A is the flow rate factor, n the flow law exponent, ρ the ice density and g the gravitational acceleration. For flow of ice confined to a channel the surface velocity on the center line of the glacier can be calculated by introducing a shape factor f (Reference NyeNye, 1965):

h is now the ice thickness at the center of the channel. Reference Kamb and EchelmeyerKamb and Echelmeyer (1986) described a method to calculate u ch for the case of longitudinally variable ice thickness and surface slope, by a method of longitudinal averaging (adapted from their equations 35a and b):

where x is the downslope longitudinal coordinate, L is the glacier’s length, and g(.) is a weighing function:
C is a normalizing factor such that ![]() and L
+ are up- and downstream averaging lengths, as calculated by Reference Kamb and EchelmeyerKamb and Echelmeyer (1986). They are typically about three times the local ice thickness. The basal speed ub
was introduced into Equation (4) in an ad hoc way, assuming that it is averaged in the same way as the deformational speed u
ch. It is of advantage to write Equation (4) as an inner product:
and L
+ are up- and downstream averaging lengths, as calculated by Reference Kamb and EchelmeyerKamb and Echelmeyer (1986). They are typically about three times the local ice thickness. The basal speed ub
was introduced into Equation (4) in an ad hoc way, assuming that it is averaged in the same way as the deformational speed u
ch. It is of advantage to write Equation (4) as an inner product:

We recast this equation into:

The lefthand side can be evaluated at discrete points xj , as it only contains quantities derivable from measurements, such as u surf and u ch. Comparing Equation (7) to Equation (1) we realize that we have defined a linear inverse problem, with dj = ln u surf (xj ) – (g, ln u ch) and m = ln(1 + u b/u ch).
As mentioned above, infinitely many solutions m satisfy Equation (7) exactly. We now need a measure to choose an optimal solution. Following Parker (1994, sec. 3.05), we accomplish this by minimizing a norm. The choice of a norm should be guided by a property of the function that is desirable. Here, we choose a norm (more correctly a semi-norm) that is a measure of the first derivative of m. Minimizing this norm will select a function with a small first derivative, i.e. a smooth function. Since solutions will be found numerically, we proceed by discretizing m, writing it as a vector in ℝ M , with M > N (the number of measurements). The calculation of the norm can then be defined through a matrix R, such that:
We will choose 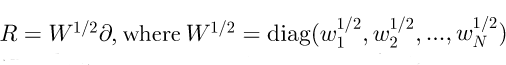 is a diagonal matrix containing the proper weighting factors for a quadrature rule integration, and
is a diagonal matrix containing the proper weighting factors for a quadrature rule integration, and

is a differencing operator. It is now possible to proceed by minimizing this norm for all m that solve Equation (7) exactly.
However, the lefthand side of Equation (7) has measurement errors associated with it, so we do not wish to solve it exactly. Instead, we require that Equation (7) be solved within a tolerance that is dictated by the errors in the data:
where ∑ is a diagonal matrix containing the standard deviations, and B = WG is the product of a weighting matrix for quadrature integration W and the Gram matrix G consisting of the discretized representers gj . T is the tolerance level, and it is strictly a function of N (Reference ParkerParker, 1994, sec. 3.01). Parker (1994, sec. 3.02) also shows that under most conditions equality holds for Equation (10). The problem now becomes one of minimizing the semi-norm (6) under condition (10). A standard method of doing that is to introduce a Lagrange multiplier v and minimize the functional:
v is sometimes called the trade-off parameter. If it is large, fitting the data within the tolerance is dominant; if it is small, then minimizing the semi-norm is more important. In that sense it defines a trade-off between norm-minimization and data fit. But in general, both v and m can be found by solving ∂U/∂mi = 0 and ∂U/∂v = 0. The second condition simply yields Equation (10) with equality.
Synthetic Glaciers
We have done controlled tests of this inverse procedure by running a forward model to create “data”, introducing some noise, and inverting the “data”. The forward model consists of a simple glacier of uniform thickness, shape and slope. The basal speed varies down-glacier (lower curve in Fig. 1). The upper solid line shows the surface speed predicted by the forward model. We then sample this at regular intervals and introduce random noise (crosses in Fig. 1). This “dataset” is used as an input to the inverse model.

Fig. 1. A forward model is used to generate “data”. The lower line is the prescribed basal speed, the upper solid line shows calculated surface speed, and the crosses show the surface speed with some random noise that is used for the inverse model. The longitudinal coordinate is normalized by the ice thickness, and the flow speed by the deformational speed that would result if the glacier was frozen to its bed.
The lower solid line in Figure 2 shows the results of the inversion, compared to the originally prescribed basal speed (lower dotted line). The basal speeds resulting from the inversion are again run through the forward model (upper solid line) and compared to the “data”. This simple example shows that a satisfactory solution can be found. Because the inverse procedure selects smooth functions, the true maxima in basal speed are under-predicted while the minima are over-predicted. Figure 2 also shows that the solution fits the data within the error.

Fig. 2. Results of the inversion (lower solid line) compared to the originally prescribed basal speed. The inversion result is again run through the forward model (upper solid line) and compared to the “data”. Normalized units are as in Figure 1.
Two things should be noted: First, in general the true basal velocities cannot be recovered. This is because of the diffusive nature of ice flow. Small-scale velocity variations can only be detected close to the glacier bed, not at the surface. This is in close agreement with results from Balise and Raymond (1986) and Reference GudmundssonGudmundsson (2003). Secondly, it would be a mistake to try to fit surface velocities exactly. Of all the models that fit the above “data”exactly (there are an infinity), the smoothest one still oscillates in an unrealistic fashion (Fig. 3). This is again due to the non-linear and diffusional nature of ice flow. If an error in a surface measurement is interpreted as a physical effect described by the model, it will require an amplified subglacial cause. This is a major problem with Van der Veen and Whillans’ (1989) force budget method. It is an appealing feature of this inverse method that measurement errors can be accommodated.

Fig. 3. The smoothest model that fits the “data” exactly. The lower curve shows the result of the inversion (solid line) compared to the originally prescribed basal speed (dotted line). The upper curve shows the “data” (crosses) and the fit of the inversion to them (solid line). Units are as in Figure 1.
As mentioned above, we cannot hope to resolve velocity variations on a small scale. There is a somewhat intuitive way to derive resolving functions to find the minimum resolving length. It is done by running a Dirac function through the forward model and then inverting the result. The Dirac 8 function is used, because it represents the smallest possible perturbation. Inverting the resulting surface speeds thus illustrates how much a small-scale basal perturbation spreads through the inversion process. The half-width of the resulting bell-shaped function gives a measure of the spatial scale at which structure in the model can be resolved (Fig. 4). This scale depends on the accuracy of the data. It is noteworthy that the resolving scale does not tend towards zero as the sampling interval for the data becomes small. The half-width of the resolving function remains at two to three ice thicknesses, even for an almost continuous record of glacier geometry and surface speed (Fig. 4; ice thickness is 200 m in this example).

Fig. 4. Resolving function for the inversion discussed above (upper line).The half-width of this function defines a resolving scale for the inverse model. The lower line illustrates how the resolution degrades for inaccurate data.
Since the inversion method presented here selects for a smooth model, it will discriminate against fast changes and spread them out over a range given approximately by the half-width of the resolving function. We illustrate this by modeling a glacier with constant thickness (200 m), slope (5°), and channel shape (f = 0.5). Basal velocities undergo a step change from 0to5ma-1 halfway down the glacier. We ran the forward model and inverted it subsequently (Fig. 5). The step change is spread over several ice thicknesses, as illustrated by the results of the inversion and the resolving function.

Fig. 5. A step change (dash-dotted line) in basal speed was run through the forward model and sampled at a regular interval (crosses).The results were then inverted (dotted line). The inversion results fit the original data well (thick solid line). The half-width of the resolving function (thin solid line) compares well to the spreading of the step change in the inversion process.
We will now apply the method to two glaciers, where suitable data have been gathered: Brown Glacier in the southern Indian Ocean, and McCall Glacier in the Brooks Range, Alaska, U.S.A.
Brown Glacier
Brown Glacier is located on the flanks of Big Ben, a 2700 m high volcano on the Australian sub-antarctic Heard Island (53°05′ S, 73°30′ E). The Australian Antarctic Division selected it for a detailed study illustrating glacier change in the Southern Hemisphere. The ensuing report (Reference Truffer, Thost and RuddellTruffer and others, 2001a) contains data on the flow and geometry of the glacier (Fig. 6). Velocities were measured at points spaced about 500 m along the 5 km long glacier (Fig. 6d). Ice thickness was only measured at four sites (Fig. 6a). The shape factor was calculated assuming a channel of parabolical shape and interpolating between the results obtained for the half-width to depth ratios calculated by Reference NyeNye (1965). Surface slope was read from a map that was created from kinematic global positioning system profiles (Reference Truffer, Thost and RuddellTruffer and others, 2001a). The slope was averaged over about one ice thickness (~100 m).

Fig. 6. Data used in the inverse model for Brown Glacier. Ice thickness (a), surface slope (b), shape factor (c) and observed surface velocities (d) are shown. Ice thickness an shape factors were only determined on the lower part of the glacier.
We restrict our analysis to the lower part of the glacier, where the ice thickness is known. All data were interpolated onto a regular grid, spaced 200 m, and this was used as an input for the inverse model, as described above. We assumed a flow rate factor of A = 3.2 × 10-24 Pa-3 s-1 in Equation (1). This value is about half that recommended by Reference PatersonPaterson (1994). Figure 7 shows the deformational speed calculated with the forward model assuming no basal motion. Note that the deformational speed would exceed observed surface speed at many locations if Reference PatersonPaterson’s (1994) value for the flow rate factor were used. This has been found to be true for many temperate glacier flow models (Reference HookeHooke, 1981; Reference Hubbard, Blatter, Nienow, Mair and HubbardHubbard and others, 1998; Reference GudmundssonGudmundsson, 1999; Adalgeirsdottir, 2000; Reference Albrecht, Jansson and BlatterAlbrecht and others, 2000; Reference Truffer, Thost and RuddellTruffer and others, 2001b). The inversion indicates steadily increasing basal motion in the lower part of the glacier (Fig. 7). As discussed above, we do not require the inversion to fit the data exactly, in order to account for errors. The actual measurement errors for the glacier speed are small (±3ma-1), but additional errors can arise due to the simplification of a one-dimensional model. Figure 7 also shows the fit of the inversion to the original data, and resolving functions at two points. These functions have a half-width of about 500 m. This defines a useful scale for the interpretation of the inversion results. Nothing should be deduced on a scale smaller than that. For example, it is possible that the actual increase in basal motion happens on a smaller scale, as demonstrated above for the step function model.

Fig. 7. Results of the Brown Glacier inversion, showing the inverted basal speed (dotted line), the deformational speed without basal motion (dash-dotted line), the surface speed calculated from the inverted results (solid line), and the observed speed (crosses). Note that the results of the inversion do not match the observations exactly. The bell-shaped curves are resolving functions at two positions. Their half-width is an indication of the spatial scale over which changes can be resolved.
McCall Glacier
McCall Glacier in Alaska’s Brooks Range has been studied intermittently since the International Geophysical Year (Reference Rabus, Echelmeyer, Trabant and BensonRabus and others, 1995, and references therein). As part of a more recent regional mass-balance study, Reference Rabus and EchelmeyerRabus and Echelmeyer (1997) described the dynamics of this polythermal glacier. They noticed that deformational speeds alone could not account for the observed surface speeds and a region of year-round basal motion must exist in the middle part of the glacier. Here, we confirm their findings by running an inverse model. We used data published by the above authors (their Fig. 10) and sampled it every 200 m. Our results show not only the sliding anomaly pointed out by Reference Rabus and EchelmeyerRabus and Echelmeyer (1997), but also a smaller one further upstream (Fig. 8). Not surprisingly, the inversion results in a smoother profile of basal speeds than that proposed by the other authors. The resolving functions show a resolving scale of about 500-700 m (or about three to four times the ice thickness). As discussed above, nothing can be said about the variation of basal motion on smaller scales, so both models for basal motion are equally plausible.

Fig. 8. Results of the McCall Glacier inversion. Inverted basal motion (dotted line), deformational speed (dash-dotted line), surface speed calculated from the inversion results (heavy thick line), and the observed surface speeds (crosses) are shown. The thin solid line shows the basal velocity that Reference Rabus and EchelmeyerRabus and Echelmeyer (1997) used to model surface velocities. The bell-shaped curves are resolving functions with half-widths of about 700 m (four to five ice thicknesses).
Conclusions
We successfully applied geophysical inverse methods to find the basal velocity of a valley glacier. The forward model is a one-dimensional theory of glacier flow down an inclined channel. It includes longitudinal stress gradients (Reference Kamb and EchelmeyerKamb and Echelmeyer, 1986) and can be used to calculate the surface speed given the glacier geometry, basal motion and the flow law. Inverse methods are then applied to calculate the basal motion, given the surface speed and glacier geometry, which is a more realistic and common situation. The inverse procedure chosen here selects for a smooth model by minimizing a norm that is a measure of the first derivative. In general, the inverse problem can be solved exactly. However, it is advantageous to relax that condition and allow the model to account for errors in the data. This prevents unphysical solutions resulting from trying to fit measurement errors, or processes not accounted for in the model. Our method also allows us to calculate so-called resolving functions. They are obtained by propagating a point perturbation through the forward and back through the inverse model. Its half-width is a qualitative measure of the minimum scale that can be resolved by the inverse method. This scale is typically three to four times the ice thickness, but can be larger if data are sparse. It depends on the averaging lengths (L + and L - in Equation (5)) and on the sampling interval for geometry and surface velocity. The averaging lengths also depend on the rate of basal motion (Reference Kamb and EchelmeyerKamb and Echelmeyer, 1986). This can be accounted for through an iterative procedure, where the averaging lengths are adjusted after a first inversion, and the inversion is then repeated with the new values.
This paper focuses on applying inverse methods to valley glacier flow, which is a problem that has seldom been addressed in the glaciological inverse literature. However, the same methods can be applied to ice sheets and ice streams, and they can be generalized, in principle, to non-linear forward models (e.g. Reference ParkerParker, 1994) and to numerical forward models. They can then be extended to two or three dimensions and applied to a variety of complex flow regimes.
Acknowledgements
I would like to thank K. Echelmeyer who sparked my interest in these methods and with whom I had many fruitful discussions. I also appreciate the input from R. Greve (Scientific Editor), H. Blatter and an anonymous reviewer. M. Luthi read the manuscript and provided useful comments. Part of this work was done while working at the Australian Antarctic Division in Hobart, Tasmania. Funding from the U.S. National Science Foundation (OPP-0115819) helped complete the study.









