1. Introduction
The filling and draining of ice-dammed reservoirs underlies many important glaciohydrological phenomena. Ice-marginal lakes fill with meltwater and can drain suddenly through subglacial channels (Reference NyeNye, 1976; Reference BjörnssonBjörnsson, 2002; Reference RobertsRoberts, 2005), producing subglacial floods called ‘jökulhlaups’ that pose hazards and impact ice dynamics (Reference Björnsson, Owens and SlaymakerBjörnsson, 2004; Reference Anderson, Walder, Anderson, Trabant and FountainAnderson and others, 2005; Reference Sugiyama, Bauder, Weiss and FunkSugiyama and others, 2007; Reference Bartholomaus, Anderson and AndersonBartholomaus and others 2008; Reference MagnússonMagnússon and others, 2011; Reference Kingslake and NgKingslake and Ng, 2013a). Englacial conduits called moulins route surface meltwater to the beds of glaciers and ice sheets, coupling ice dynamics to surface meteorological conditions (e.g. Reference Nienow, Sharp and WillisNienow and others, 1998; Reference Zwally, Abdalati, Herring, Larson, Saba and SteffenZwally and others, 2002; Reference BartholomewBartholomew and others, 2011; Reference CowtonCowton and others, 2013; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014). Subglacial lakes at the beds of ice sheets reduce basal friction and influence basal conditions as they drain (e.g. Reference Wingham, Siegert, Shepherd and MuirWingham and others, 2006; Reference Bell, Studinger, Shuman, Fahnestock and JoughinBell and others, 2007; Reference DasDas and others, 2008; Reference StearnsStearns and others, 2008; Reference Wright and SiegertWright and Siegert, 2012; Reference Carter, Fricker and SiegfriedCarter and others, 2013; Reference SergienkoSergienko, 2013; Reference Howat, Porter, Noh, Smith and JeongHowat and others, 2015).
The filling and drainage of these ice-dammed reservoirs is controlled by the imbalance between two water fluxes: input controlled predominantly by meltwater production and output through a subglacial drainage system whose evolution is controlled by the water pressure in the reservoir. Hence these reservoirs are coupled to subglacial drainage systems in terms of water pressure and discharge (Reference NyeNye, 1976; Reference NgNg, 1998; Reference Flowers, Björnsson, Pálsson and ClarkeFlowers and others, 2004; Reference EvattEvatt, 2006; Reference Kingslake and NgKingslake and Ng, 2013a).
Reference NyeNye’s (1976) model of an ice-dammed lake that drains through a subglacial channel to produce jökulhlaups was the first mathematical description of this coupling. It has been used to investigate various aspects of jökulhlaup dynamics (e.g. Reference Spring and HutterSpring and Hutter, 1981; Reference ClarkeClarke, 1982, Reference Clarke2003; Reference BjörnssonBjörnsson, 1992, Reference Björnsson1998; Reference NgNg, 1998; Reference FowlerFowler, 1999, Reference Fowler2009; Reference JóhannessonJóhannesson, 2002; Reference Ng and BjörnssonNg and Björnsson, 2003; Reference Kessler and AndersonKessler and Anderson, 2004; Reference EvattEvatt, 2006; Reference Ng and LiuNg and Liu, 2009; Reference Pimentel and FlowersPimentel and Flowers, 2011; Reference Kingslake and NgKingslake and Ng, 2013a; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014). In particular, Reference FowlerFowler (1999) showed that a modified version of Reference NyeNye’s (1976) model can simulate stable, periodic flood cycles when a constant water input is supplied to the lake and the subglacial channel along its length (Reference EvattEvatt, 2006; Reference Kingslake and NgKingslake and Ng, 2013a). Reference FowlerFowler (1999) also showed that modelled floods are larger when the constant input to the lake is larger. This is due to the dynamics of a subglacial hydraulic divide that forms during lake-filling periods and could explain observed variability in the size of floods (Reference Ng, Liu, Mavlyudov and WangNg and others, 2007; Reference Ng and LiuNg and Liu, 2009; Reference KingslakeKingslake, 2013; Reference Kingslake and NgKingslake and Ng, 2013b).
Most previous jökulhlaup modelling studies have used a constant lake input. This is unrealistic. Real ice-dammed reservoirs receive water inputs that vary on diurnal, seasonal and interannual timescales (e.g. Reference Bartholomaus, Anderson and AndersonBartholomaus and others 2008; Reference Ng and LiuNg and Liu, 2009; Reference Kingslake and NgKingslake and Ng, 2013b; Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others, 2014; Reference Siegfried, Fricker, Roberts, Scambos and TulaczykSiegfried and others, 2014). Here we investigate the behaviour of Reference NyeNye’s (1976) model when it is forced with a meltwater input that depends on a seasonally varying synthetic air temperature time series. Section 2 describes the model, this seasonally varying forcing, our numerical methods and a suite of numerical simulations during which the magnitude of air temperature variations is varied between simulations. In Section 3 we present the results of these simulations and show that simulated flood cycles can be ‘mode-locked’, so that their repeat time equals an integer multiple of the forcing period (1 year), and ‘resonate’ when forced with air temperature variations of particular magnitudes. We also show that the model can behave chaotically, where simulated time series are highly sensitive to initial conditions and never repeat exactly, despite idealized model geometry and forcings. Abrupt changes in flood characteristics, or ‘bifurcations’, separate regions of parameter space associated with these behaviours. In Section 4 we discuss the implications of our findings for real ice-marginal lakes, moulins and subglacial lakes.
2. Methods
2.1. Model
Our model closely resembles that described by Reference FowlerFowler (1999). It consists of a subglacial channel hydraulically coupled (in terms of both water discharge and pressure) to an ice-dammed lake (Fig. 1). The most important difference between our model and Fowler’s is our addition of a seasonally varying lake input. Model variables and parameters are summarized in Tables 1 and 2.

Fig. 1. Our model ice-dammed reservoir system. (a) A subglacial channel is hydraulically coupled to an ice-dammed lake that receives meltwater at a rate Q i. The channel receives a constant and uniform supply of water along its length M. (b) The prescribed basic hydraulic gradient ψ (blue curve) is negative near the lake – a topographic seal. Also displayed is an example pair of ice surface and bed profiles (z s and z b; black and brown curves) that would produce this hydraulic gradient. In this example the bed slope φ b = 0.01.
Table 1. Summary of model variables

Table 2. Model parameters and physical constants

The ice-dammed lake is vertically sided, with a surface area A = 5 km2, and the ice dam has a constant thickness H =100 m. Its depth h L evolves with time t due to input Q i and water exchange with the subglacial channel (Fig. 1) according to
where Q is the discharge in the channel and the spatial coordinate s is zero at the lake and s 0 (=10 km) at the glacier terminus. The lake’s depth provides the boundary condition on the channel’s effective pressure N (equal to the difference between the ice-overburden and water pressures) at the lake outlet: N(0,t) = ρ i gH − ρ w gh L, where ρ i is the ice density (900 kg m−3), ρ w is the water density (1000 kg m−3) and g is the acceleration due to gravity (9.8 m s−2). One choice for the boundary condition on N at s = s 0 is N(s 0,t) = 0 (e.g. Reference NgNg, 1998; Reference KingslakeKingslake, 2013). However, to simplify the numerics, we assume that drainage is controlled by a boundary layer in the channel’s effective pressure near the lake. Hence this boundary condition is replaced by ∂N/∂s = 0 (Reference FowlerFowler, 1999). The qualitative behaviour of the model is not affected by this simplification (Reference EvattEvatt, 2006; Reference KingslakeKingslake, 2013).
The evolution of the channel’s cross-sectional area is controlled by the competition between melt enlargement and creep closure:
where n = 3 and K 0 = 10−24 Pa−3 s−1 are temperate ice-rheology parameters (Reference FowlerFowler, 1999) and m is the rate of frictional channel-wall melting per unit distance ((ψ + ∂N/∂s)|Q|/L, where L is the latent heat of fusion of water (334 kJ kg−1) and ψ is the basic hydraulic gradient). This assumes that the water is at the pressure-melting point and all the energy it gains as it flows through the total hydraulic gradient (ψ +∂N/∂s) is used locally for melting (Reference FowlerFowler, 1999). Ignoring a small contribution from the changing channel area, water mass continuity gives
where M is a constant, uniform input to the channel along its length (7 × 10−4 m2 s−1). We use Manning’s equation to parameterize momentum balance in the turbulent water flow:
where f is the hydraulic roughness (n′2(l 2/S)2/3 ≈ 0.07 m2/3 s2 for a semicircular channel with wetted perimeter l and Manning’s roughness coefficient n′ = 0.1 m1/3 s; Reference FowlerFowler, 1999; Reference Kingslake and NgKingslake and Ng, 2013a). Water flow is driven by the total hydraulic gradient ψ + ∂N/∂s. This contains a dynamic component ∂N/∂s and a component that depends on glacier shape – the basic hydraulic gradient ψ (= ρ w g sin φ b − ∂P i/∂s, where φ b is the channel slope and P i is the ice overburden pressure). To encourage the simulation of stable flood cycles, the prescribed glacier shape is such that ψ is negative near the lake (Fig. 1b):

where ψ 0 = 100 Pa m−1.
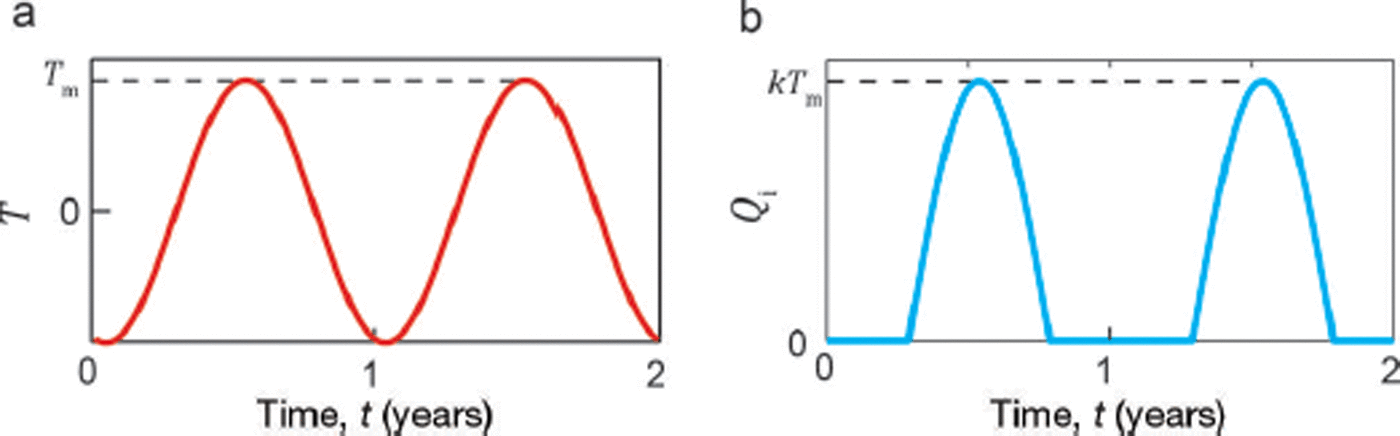
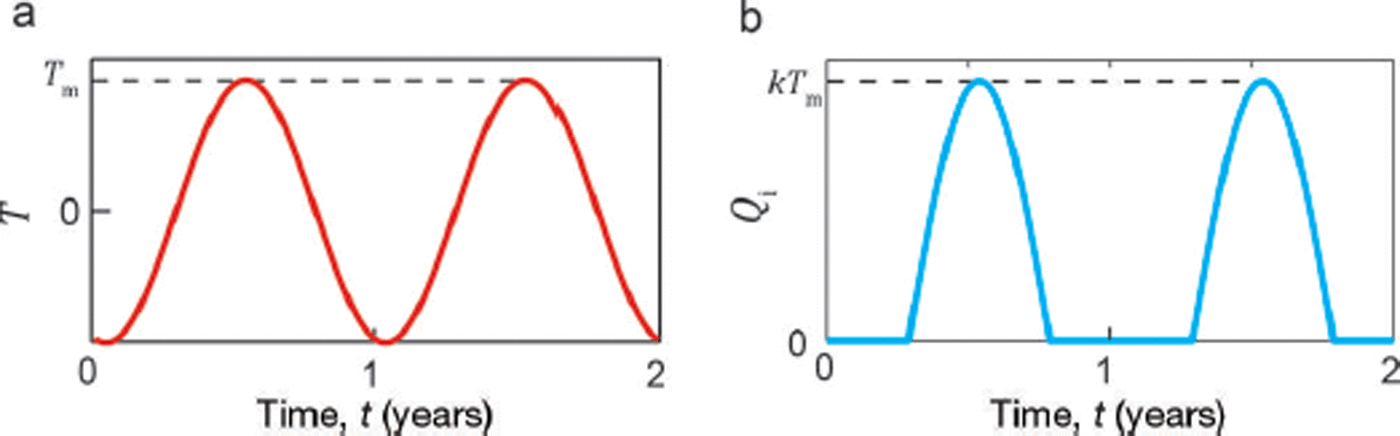
To simulate seasonal weather variations and drive a simple model of lake input Q i we use a synthetic sinusoidal air temperature time series,
where t has units of years and integer t corresponds to the beginning of each calendar year. The 0.29 year offset ensures the maximum air temperature T m occurs in midsummer. We model meltwater input to the lake Q i by

where k = 2 m3 s−1 K−1, close to the value of a similar parameter derived empirically by Reference Kingslake and NgKingslake and Ng (2013b). Figure 2 plots our synthetic air temperature time series, as defined by Eqn (6), and the corresponding time series of meltwater input to the lake, as defined by Eqn (7).
2.2. Parameters
The model includes several physical parameters that are poorly constrained by observations (Table 2). The Manning’s roughness coefficient n′ = 0.1 m1/3 s and the ice-rheology parameters n and K 0 are chosen based on previous similar studies (Reference FowlerFowler, 1999; Reference Evatt, Fowler, Clark and HultonEvatt and others, 2006; Reference Kingslake and NgKingslake and Ng, 2013a). The constant supply of water to the channel along its length M = 7 ×10−4 m2 s−1 implies a reasonable background terminus discharge of s 0 M = 7 m3 s−1. We expect the results of our analysis not to depend qualitatively on these parameter values.
To parameterize the basic hydraulic gradient, Reference FowlerFowler (1999) proposed Eqn (5) based on observations of ice thickness from Vatnajökull, Iceland (Reference BjörnssonBjörnsson, 1992). An area of negative hydraulic gradient near the lake, or ‘topographic seal’, encourages stable flood cycles in the model via the formation of a subglacial hydraulic divide. Reference KingslakeKingslake (2013) and Reference Kingslake and NgKingslake and Ng (2013a) showed that a topographic seal is not a requirement for divide formation or for the simulation of stable flood cycles. We impose a topographic seal in this study to increase the range of parameter space over which stable flood cycles can be simulated. Qualitatively the model’s behaviour is independent of the details of the seal (Reference KingslakeKingslake, 2013).
The formation of the hydraulic divide does require a nonzero channel input M, because when M = 0, Q is uniform (Eqn (3)). Without the stabilizing effect of divide formation, simulated floods grow unstably (Reference NgNg, 1998; Reference FowlerFowler, 1999; Reference KingslakeKingslake, 2013; Reference Kingslake and NgKingslake and Ng, 2013a). This is unrealistic, therefore we use a positive channel input M to allow us to simulate stably repeating floods.
2.3. Numerics
To explore the behaviour of the model we solve its governing equations numerically. Space and time domains are discretized with a grid spacing of 100 m and time steps of 2.7 hours. Integrating Eqn (3) and combining the result with the terminus boundary condition on N and Eqn (4) yields
With Q calculated using this expression, N is found by integrating Eqn (4) from the lake, where N is determined by the lake depth (N(0,t) = ρ i gH − ρ w gh L), to the terminus. With Q and N known everywhere, h L and S are evolved forward in time using Eqns (1) and (2) and the forward Euler method, with Q i given by Eqns (6) and (7). Reference FowlerFowler (1999), Reference EvattEvatt (2006) and Reference KingslakeKingslake (2013) provide more details.
2.4. Experimental design
We conduct a suite of numerical model simulations during which the parameter T m is varied systematically (0.1 ≤ T m ≤ 28°C) between simulations and kept constant during each simulation. During this exploration of T m parameter space, all other parameters are kept constant. Unless otherwise stated, all the simulations start with h L = 40 m and a uniform channel cross-sectional area ∼5m2, and continue for 120 model years.
3. Results
To demonstrate several interesting aspects of the model’s behaviour, we first discuss the results of three simulations that lie in three crucial regions of T m parameter space. The model produces qualitatively different flood cycles in each region and we present the results in the form of time series of lake input and discharge, and phase-space portraits that plot lake discharge against lake level. Next we plot the peak discharge of all the floods in all our simulations against the parameter T m used to simulate them. This reveals regions of parameter space associated with mode locking, resonance and chaos, and the abrupt transitions, or bifurcations, that separate them. Finally we investigate the properties of chaotic model solutions and two types of bifurcation.
3.1. Flood cycles
Figure 3 plots flood cycles simulated using three different values of the midsummer air temperature T m. Figure 3a, c and e display 20 year time series of discharge at the lake outlet, Q(0,t), extracted from the results of three simulations that use T m = 10°C, T m = 12.7°C and T m = 15°C. Figure 3b, d and f show corresponding orbits in Q(0,t)−h L(t) phase space.

Fig. 3. Simulated flood cycles. Results from three simulations using seasonally varying air temperatures to drive lake input, with (a, b) T m = 10°C, (c, d) T m = 12.7°C and (e, f) T m = 15°C. (a, c, e) Time series of discharge at the lake outlet Q(0,t) (blue curves) and lake input Q i(t) (green curves) for 20 model years after transients have ended. (b, d, f) Solution orbits in Q(0,t)−h L(t) phase space from the complete 120-year-long simulations.
When T m = 10°C and 15°C, after transients, the system approaches limit cycles with repeat times of 2 years and 1 year respectively (Fig. 3a and e). The sequence of lake filling, channel enlargement through melt, lake highstand and drainage has been described elsewhere (Reference NyeNye, 1976; Reference FowlerFowler, 1999, Reference Fowler2009; Reference Ng and BjörnssonNg and Björnsson, 2003; Reference Kingslake and NgKingslake and Ng, 2013a). Note that the discharge at the lake outlet is negative between floods; a hydraulic divide forms in the channel near the lake. Reference FowlerFowler (1999) showed how the dynamics of this divide cause flood size to increase with Q i when this input is kept constant (Reference KingslakeKingslake, 2013: ch. 3). Contrary to expectations based on these previous analyses, the warmer simulation (T m = 15°C; Fig. 3e and f), with the higher mean lake input, produces flood cycles with a lower peak discharge (cf. Fig. 3a and e).
When T m = 12.7°C, flood cycles are simulated but they do not approach limit cycles (Fig. 3c and d). Instead the cycles appear random, never reaching a repeating orbit in Q(0,t)−h L(t) phase space (Fig. 3d). We will show that these cycles exhibit chaotic characteristics.
3.2. Mode locking
Figure 4 plots the results of many simulations during which we record the peak discharge of each flood. Each point in Figure 4 plots one flood’s peak discharge (vertical axis) against the value of T m used in the simulation that produced that flood (horizontal axis). The colour of each point indicates the day of the year on which the flood peak occurred.

Fig. 4. T m parameter space. (a) Peak discharge of floods recorded during 120 year simulations plotted against the value of the midsummer air temperature T m used in each simulation. The first ten flood peaks of each simulation are omitted to remove transients. The black box indicates the region shown in more detail in (b). Horizontal quantization visible in (a) (T m > 16°C) is the result of a coarse search through this region. The vertical lines in (b) correspond to orbits plotted in Figure 9. Lines that are one point in vertical extent (e.g. 6 ≤ T m ≤ 11°C and T m > 19°C) correspond to limit cycles, where all the recorded floods have the same peak discharge; slightly thicker lines (e.g. 14 ≤ T m ≤ 17°C) correspond to simulations during which transients lasted longer than ten flood cycles; and large blocks of points indicate dense, chaotic orbits. The colour of each point indicates the day of the year on which the flood peak occurs. In (a) the green arrows indicate two regions where floods occur progressively later in the year as T m decreases.
In the regions of T m parameter space around T m = 10°C and T m = 15°C, floods occur progressively later in the year as T m decreases (green arrows; Fig. 4a). Moreover, instead of floods occurring less often as T m decreases, the mean time between floods (hereafter referred to as the repeat time) remains constant and peak discharges decrease to compensate for the decrease in time-averaged lake input (Fig. 4a).
This behaviour is analogous to ‘mode locking’ of periodically forced nonlinear oscillators, when the frequency of an oscillator’s response stays locked to that of the frequency of the forcing. This can occur when the frequency of the forcing is comparable to an oscillator’s natural frequency. Similarly, the mode-locking behaviour of our model only manifests when the timescales of the lake-depth and subglacial-channel evolution, predominantly controlled by the lake surface area and glacier geometry respectively (Section 2), are comparable to the periodicity of the time-varying meltwater input (1 year).
3.3. Resonance
As T m decreases from 15°C to 10°C, the peak discharges of floods increase and their timing in the year shifts abruptly (Fig. 4). When the lake’s total annual input V A is slightly too large to allow it to persist for 2 years before draining (e.g. when T m = 15°C), relatively small floods occur every year. When T m is smaller (e.g. when T m = 10°C) the lake can persist for 2 years before draining. Although the time-averaged lake input is now lower, the flood repeat time is twice as large (2 years instead of 1 year). Hence the total input to the lake between each flood is increased. This increases flood peak discharges.
Floods are largest when the climatic forcing allows the lake to fill completely in an integer number of years. A lake’s ‘resonant climatic forcing’ is any value of T m that allows the lake basin to fill completely over n years, where n = 1, 2, 3, etc. Therefore, there exist multiple resonant values of T m corresponding to V A = V F/n, where V F is the lake’s volume when full. This is reflected in Figure 4 by a second resonance peak at T m ≈ 5.5°C and a third at T m ≈ 2°C (not clearly visible at the resolution of Fig. 4). Integrating Eqns (6) and (7) yields V A =3.15 × 107 kT m/π. Assuming the lake fills to the flotation level (9/10H) before emptying completely during each flood (V F = 9/10HA), the nth resonant climatic forcing is given by T m n = 0.9πHA/(3.15 × 107 kn) = {22.4, 11.2, 7.5, 5.6,…}°C. The second resonant T m value (11.2°C) matches the numerically simulated resonance peak (Fig. 4). However, when T m < 10°C, a significant volume of water is left in the lake after floods and this simple analysis fails.
3.4. Chaotic dynamics
Mode-locked regions of parameter space are separated by densely populated regions (Fig. 4) corresponding to dense periodic orbits that never repeat. These orbits are sensitive to their initial conditions. Figure 5a plots time series of lake depth from two simulations that used T m = 12.7°C, with two slightly different initial lake depths, 40.00 m and 40.01 m. Figure 5b and c plot the trajectories of the two solutions in three-dimensional (3-D) discharge–lake-depth–channel-size (Q(0,t)−h L(0)−S(0,t)) phase space, while Figure 5d shows the normalized separation of these orbits. The solutions track each other for ∼15 years before diverging. However, their separation does not grow unboundedly; they remain in the same region of phase space (Fig. 5b and c), but despite approaching each other at t ≈ 65 years (Fig. 5d) they never collapse onto a common orbit. This behaviour is indicative of chaotic dynamics and has been studied thoroughly in other fields (e.g. Reference DrazinDrazin, 1992; Reference OttOtt, 2002).

Fig. 5. Sensitivity to initial conditions. (a) Time series of lake depth from two simulations which used T m = 12.7°C. Simulations are identical except for a slight difference in their initial lake depth h L(0). The blue curve corresponds to h L(0) = 40.00 m, and the red curve corresponds to h L(0) = 40.01 m. (b, c) Corresponding orbits in Q(0,t)−h L(0)–S(0,t) phase space, with the initial and final conditions shown in green and red respectively. (d) Time series of the normalized separation between the orbits in (b, c). Normalized separation is calculated by differencing each component of the orbits’ positions normalized with the maximum value of the corresponding variable. The Pythagorean sum of the normalized separation is plotted. Note the different time axes in (a) and (d).
Another indicator of chaotic dynamics is topological mixing of phase space, where orbits fold and bifurcate, visiting every part of a specific region of phase space. Figure 6 plots the trajectory of one simulation (with T m =12.7°C) in another 3-D phase space: discharge–lake-depth–time (Q(0,t)−h L(t)−t) space. Figure 6b displays two-dimensional Poincaré sections taken along Q(0,t)−h L(t) planes, perpendicular to the t-dimension, at nine instants in the annual cycle. The trajectory possesses a clear structure; together the points form a shape called an attractor. The ‘Nye attractor’ rotates, bifurcates and folds over on itself as the sections progress through the annual cycle. This depiction of topological mixing is reminiscent of equivalent plots from studies of nonlinear oscillators (e.g. the Duffing oscillator; Reference Novak and FrehlichNovak and Frehlich, 1982).

Fig. 6. The Nye attractor and topological mixing of phase space. (a) A solution orbit in Q(0,t)−h L(t)−t phase space of a simulation that used T m = 12.7°C and h L(t = 0) = 40 m. The blue curve’s distance from the vertical green line denotes the lake depth h L(t), its position along the vertical axis denotes the discharge at the lake Q(0,t) and its rotation around the green line denotes the fractional part of time t multiplied by 2π (one rotation corresponds to 1 year). (b) Poincaré sections taken perpendicular to the t-dimension at nine different stages of the year, denoted by the day of the year d. The points locate the intersection of the orbit with each section. Each section’s location in Q(0,t)−h L(t)−t space is indicated by the boxes in (a). The colour of the points indicates simulation time t.
3.5. Bifurcations
The transition from limit cycles to chaotic cycles around 13 < T m < 14°C involves two types of bifurcation (Fig. 4). The first, at T m ≈ 13.88°C, is an abrupt transition from period-1 orbits (i.e. limit cycles that complete one orbit before repeating) to period-2 orbits (i.e. limit cycles that complete two orbits before repeating). Figure 7 displays the orbits in Q(0,t)−h L(t) phase space of two simulations which lie on each side of this transition in parameter space. Figure 8 plots corresponding time series of Q i and Q(0,t).

Fig. 7. Orbits in Q(0,t)−h L(t) phase space of solutions with (a) T m = 13.888000°C and (b) T m = 13.888002°C, which lie on each side of an abrupt bifurcation in T m parameter space (Fig. 4) for 20 ≤ t ≤ 90 years. Points are colored to indicate simulation time t and are separated by ∼4.5 model days.
Both simulations start on almost identical unstable period-2 orbits (blue points in Fig. 7), in which every second flood is double-peaked (Fig. 8a; note that the two orbits appear as one curve in Fig. 8a). The onset of melt in spring occurs just after the first peak and instigates the second (Fig. 8a). Larger floods occur every third winter. The simulations leave these orbits in two different ways.

Fig. 8. Time series of lake input Q i and discharge through the lake outlet Q(0,t) from two simulations that lie close to the abrupt bifurcation at T m ≈ 13.88°C. (a) Initial Q i(t) and Q(0,t) time series from two simulations that used T m = 13.888000°C and T m = 13.888002°C. (b, c) Long-time time series of the same variables from simulations that used T m = 13.888000°C and T m = 13.888002°C respectively.
During the warmer simulation (T m = 13.888002°C), floods occur progressively earlier each year and the double-peaked flood evolves into two floods of equal size (Fig. 8c). Meanwhile, the originally larger flood shrinks. The result is limit cycles with a repeat time of 1 year consisting of equally sized floods (red points, Fig. 7b; Fig. 8c). During the cooler simulation (T m = 13.888000°C), floods occur progressively later until the first peak of the double-peaked flood shrinks and disappears, resulting in limit cycles where every other flood is roughly twice as large as the others and the mean flood repeat time is 1.5 years (red points, Fig. 7a; Fig. 8b).
After this abrupt bifurcation, further decrease in T m leads to a cascade of period-doubling bifurcations. Figure 9 plots four solution orbits in Q(0,t)−h L(t) phase space corresponding to T m values that bracket several period-doubling bifurcations (vertical solid lines in Fig. 4b). As T m is decreased past each bifurcation, the orbit split into two branches and the period of the orbit doubles. Many such bifurcations lead to the densely populated chaotic region on the left of Figure 4b.

Fig. 9. Period-doubling bifurcations. Long-time solution orbits (transients have been removed) in Q(0,t)−h L(t) phase space of four simulations that used (a) T m = 13.701°C, (b) T m = 13.401°C, (c) T m = 13.201°C and (d) T m = 13.151°C. (a–d) correspond respectively to the positions in T m-parameter space indicated in Figure 4b by the vertical lines A–D.
4. Discussion
When it is forced with constant meltwater inputs, Reference NyeNye’s (1976) jökulhlaup model simulates floods whose magnitudes increase with the input to the lake; the faster a lake is supplied with water, the larger the floods it produces (Reference ClarkeClarke, 1982; Reference FowlerFowler, 1999; Reference Ng, Liu, Mavlyudov and WangNg and others, 2007; Reference KingslakeKingslake, 2013). We have demonstrated a more complex relationship between meltwater input and flood size by prescribing a more realistic, time-varying lake input. Interactions between the timing of lake drainage and a seasonal cycle of lake input produce mode locking, resonance and chaotic dynamics, behaviours also exhibited by theoretical and observed nonlinear oscillators forced periodically (Reference Moon and HolmesMoon and Holmes, 1979; Reference Novak and FrehlichNovak and Frehlich, 1982; Reference DrazinDrazin, 1992; Reference KanamaruKanamaru, 2007). Their discovery in a glaciohydraulic model is interesting mathematically and may have implications for our understanding and the predictability of real-world ice-dammed reservoirs.
In comparison to real systems our model is simple. It neglects the glacier-wide subglacial drainage system and its winter shutdown, lake sensible heat, the pressure dependence of the melting point of ice, glaciological processes influencing ice-dam geometry and the coupling of glacier flow with drainage. Some models have considered some of these complications (e.g. Reference ClarkeClarke, 2003; Reference Flowers, Björnsson, Pálsson and ClarkeFlowers and others, 2004; Reference FowlerFowler, 2009; Reference HewittHewitt, 2011; Reference Pimentel and FlowersPimentel and Flowers, 2011; Reference KingslakeKingslake, 2013; Reference Kingslake and NgKingslake and Ng, 2013a; Reference Werder and JoughinWerder and Joughin, 2013; Reference Werder, Hewitt, Schoof and FlowersWerder and others, 2013) and future work could incorporate them into a more realistic jökulhlaup model. At present, our results cannot be assessed quantitatively against real jökulhlaup systems, not least because our meltwater input model (Eqn (7)) and our prescription of a constant supply of water to the channel along its length are too simplistic. However, our simple approach considering only the essential physics has revealed underlying dynamics of jökulhlaup-like systems that would be difficult to tease out from the behaviour of a more complex model.
Changes in the meltwater input to real ice-dammed lakes affect the size and timing of floods. While a jökulhlaup system remains mode-locked these changes should occur gradually and predictably (e.g. T m > 13°C; Fig. 4). Gradual timing shifts have been observed at Merzbacher Lake, Kyrgyzstan (Reference Ng and LiuNg and Liu, 2009), and Gornersee, Switzerland (Reference Huss, Bauder, Werder, Funk and HockHuss and others, 2007), with annual floods occurring progressively earlier in the year. These shifts in flood timing are consistent with long-term increases in meltwater production and our results suggest that jökulhlaup systems are also capable of undergoing more abrupt changes in both the timing and the peak discharge of floods.
These abrupt changes and the other complicated dynamics our model exhibits are produced purely by the system’s internal mechanisms; the model’s geometry and forcings are idealized and are kept constant during simulations and yet, in some areas of parameter space, simulated time series appear random, never repeat and are sensitive to initial conditions. Combined with chaotic variations in weather forcing, these dynamics may compound the difficulties of flood prediction associated with uncertain flood-triggering mechanisms and meteorological inputs (Reference Ng and LiuNg and Liu, 2009; Reference Kingslake and NgKingslake and Ng, 2013b) and make long-term prediction of flood timing difficult. Due to their sensitive dependence on initial conditions, chaotic systems are practically unpredictable beyond a certain time in the future (e.g. Reference OttOtt, 2002). However, Reference Kingslake and NgKingslake and Ng (2013b) showed that useful prediction of an upcoming flood is possible. Consideration of the dynamics revealed in the present work could help with efforts to predict the long-term evolution of mountain jökulhlaup systems (e.g. Reference Ng, Liu, Mavlyudov and WangNg and others, 2007; Reference Shen, Wang, Shao, Mao and WangShen and others, 2007).
To exhibit mode locking, resonance and chaos, a subglacially draining ice-dammed reservoir requires its input, water depth and subglacial drainage system to evolve on comparable timescales. Suppose, for example, our model jökulhlaup system was forced with a diurnally varying meltwater input. These interesting dynamics would not operate. Lake filling would be intermittent and flood discharge would contain a diurnally varying component, but qualitatively the system would behave identically to a system forced with a constant lake input equal to the time-averaged value of the diurnally varying input. Equally, a jökulhlaup lake several orders of magnitude smaller in area than the one we simulate would fill and drain too quickly for a seasonally varying forcing to induce mode locking, resonance or chaotic dynamics.
Taking into account this requirement on the evolution timescales of reservoir input, depth and drainage, should we expect to find similar dynamics in other ice-dammed reservoir systems? Moulin drainage timescales could fulfil this requirement. Moulins receive diurnally varying inputs and are typically much narrower than jökulhlaup lakes, so the water depth and meltwater input could vary on similar timescales. Furthermore, the e-folding timescale of the size of a channel that closes under the overburden pressure of an ice sheet of thickness H = 500 m is (K 0 ρ i gH)−3 ≈ 0.1 day (Eqn (2)). Beneath Antarctica, meltwater production, un-coupled from surface conditions, may evolve more slowly than subglacial lakes fill and drain, which occurs over months to years (e.g. Reference Wingham, Siegert, Shepherd and MuirWingham and others, 2006; Reference Siegfried, Fricker, Roberts, Scambos and TulaczykSiegfried and others, 2014). However, lakes can be hydraulically connected over large distances (e.g. Reference Fricker and ScambosFricker and Scambos, 2009). Hence, a downstream lake could be supplied by an upstream periodically draining lake with an input that varies on timescales conducive to chaotic dynamics. A full analysis of these two important ice-dammed reservoir systems using our model is needed to assess their ability to exhibit these complex dynamics.
Can these dynamics be detected in real systems? Reference Schoof, Rada, Wilson, Flowers and HaseloffSchoof and others (2014) observe basal water pressure variations with a 2 day repeat time in regions of the bed supplied with diurnally varying meltwater inputs through moulins. Their analysis suggests that this is a manifestation of dynamics similar to the mode locking and resonance we have discussed. This could be investigated further using our model. Other data pertaining to moulin drainage and basal water pressures (e.g. Reference Bartholomaus, Anderson and AndersonBartholomaus and others, 2008; Reference BartholomewBartholomew and others, 2011; Reference ChandlerChandler and others, 2013; Reference AndrewsAndrews and others, 2014) may contain further evidence of these dynamics that has not yet been detected.
To search for chaotic dynamics in real systems, time series covering many drainage cycles are required. Even the longest existing records of jökulhlaup, moulin and subglacial lake drainage may be insufficient (e.g. Reference Huss, Bauder, Werder, Funk and HockHuss and others, 2007; Reference BartholomewBartholomew and others, 2011; Reference Kingslake and NgKingslake and Ng, 2013b; Reference Siegfried, Fricker, Roberts, Scambos and TulaczykSiegfried and others, 2014). Moreover, evidence of fine-scale chaotic structure in real time series may be obscured by chaotic weather fluctuations (Reference Ng and LiuNg and Liu, 2009). Despite these issues, future analyses of ice-dammed reservoir systems could benefit from an appreciation of these systems’ ability to generate complex drainage time series when they behave like forced nonlinear oscillators.
5. Summary
We have shown that a model ice-dammed reservoir coupled to a subglacial drainage system can display mode locking, resonance and chaotic dynamics. These dynamics may be important for the long-term evolution and predictability of jökulhlaup systems and could manifest in other ice-dammed reservoir systems such as moulins and subglacial lakes. Understanding jökulhlaups is important for hazard mitigation, and moulins and subglacial lakes are key components in the coupling between hydrology and ice dynamics. These findings suggest that under some circumstances ice-dammed reservoirs and the glacial systems in which they play a role can undergo abrupt transitions and may be unpredictable in the long term.
Acknowledgements
I acknowledge the support of a University of Sheffield PhD studentship and the British Antarctic Survey (BAS) Polar Science for Planet Earth programme. Thank you to many people including Felix Ng, Alex Robel, Christian Schoof and Mauro Werder for discussions. I also thank Robert Arthern and Richard Hindmarsh for discussions and for commenting on the manuscript. Finally, I thank Helen Fricker and two anonymous reviewers for comments which improved the clarity of the paper.