Introduction
The absorption of solar radiation is a major component of the energy budget of the snowpack (Reference Van den Broeke, Reijmer, Van As, Van de Wal and OerlemansVan den Broeke and others, 2005; Reference Gardner and SharpGardner and Sharp, 2010). The amount of energy absorbed by the snowpack is determined by the albedo, and, because snow is translucent in the visible and near-infrared range, the localization of absorption depends on the light e-folding depth at all wavelengths of the solar spectrum (Reference WarrenWarren, 1982). The vertical profile of energy absorption controls the temperature profile in the upper snowpack (Reference SchlatterSchlatter, 1972; Reference ColbeckColbeck, 1989; Reference Brandt and WarrenBrandt and Warren, 1993; Reference Kuipers MunnekeKuipers Munneke and others, 2009), which, in turn, drives snow metamorphism close to the surface (Reference ColbeckColbeck, 1989; Reference Alley, Saltzman, Cuffey and FitzpatrickAlley and others, 1990; Reference Picard, Domine, Krinner, Arnaud and LefebvrePicard and others, 2012). The vertical profile of energy absorption also drives the temperature at the air/snow interface (Reference Flanner and ZenderFlanner and Zender, 2005; Reference Kuipers MunnekeKuipers Munneke and others, 2009). Radiation penetration is a key component for snow photochemistry, especially in the ultraviolet (e.g. Reference FranceFrance and others, 2011; Reference ErblandErbland and others, 2012). It is thus crucial to understand the dependence of solar radiation penetration on snow physical properties.
The propagation of light in snow has been extensively investigated with radiative transfer models (Reference SchlatterSchlatter, 1972; Reference Wiscombe and WarrenWiscombe and Warren, 1980; Reference ChoudhuryChoudhury, 1981; Reference BohrenBohren, 1987; Reference Flanner and ZenderFlanner and Zender, 2005; Reference Aoki, Kuchiki, Niwano, Kodama, Hosaka and TanakaAoki and others, 2011), where snow is usually represented as a collection of independent geometrical ice particles. Although snow has a complex microstructure, possibly anisotropic (e.g. Reference CalonneCalonne and others, 2012), the granular representation is computationally less demanding and has proved efficient for albedo modeling (e.g. Reference Grenfell, Warren and MullenGrenfell and others, 1994; Reference CarmagnolaCarmagnola and others, 2013). Such models, based on the granular assumption, compute the albedo and vertical profiles of irradiance in snow using the physical characteristics of snow (e.g. density, grain size, grain shape and amounts of light-absorbing impurities). While the impact of grain size and density on snow macroscopic optical properties has been extensively studied (e.g. Reference Giddings and ChapelleGiddings and LaChapelle, 1961; Reference Bohren and BarkstromBohren and Barkstrom, 1974; Reference Wiscombe and WarrenWiscombe and Warren, 1980), fewer studies discuss the impact of grain shape on these optical properties (Reference Sergent, Leroux, Pougatch and GuiradoSergent and others, 1998; Reference Grenfell and WarrenGrenfell and Warren, 1999; Reference Ba¨nninger, Bourgeois, Matzl and SchneebeliBa¨nninger and others, 2008; Reference LiboisLibois and others, 2013). In most models of radiative transfer in snow, grains are considered to be spherical (Reference Wiscombe and WarrenWiscombe and Warren, 1980; Reference Flanner and ZenderFlanner and Zender, 2005) but this representation has proved inadequate to match irradiance measurements in snow (Reference Bohren and BarkstromBohren and Barkstrom, 1974; Reference Sergent, Chevrand, Lafeuille and MarboutySergent and others, 1987; Reference Meirold-Mautner and LehningMeirold-Mautner and Lehning, 2004). Reference LiboisLibois and others (2013) show that the decrease of irradiance in snow with depth is strongly dependent on grain shape. In their radiative transfer model, TARTES, based on the theoretical framework of Reference Kokhanovsky and ZegeKokhanovsky and Zege (2004), grain shape is represented by two parameters, the absorption enhancement parameter, B, and the geometric asymmetry factor, g G. The absorption enhancement parameter, B, quantifies the lengthening of the photon path within a grain due to internal multiple reflections. It relates the grain absorption cross section, C abs, to its volume, V: C abs = Bγ V, where γ is the ice absorption coefficient. The geometric asymmetry factor, g G, measures the ratio between forward and backward scattering by the grains. These two shape parameters directly impact snow optical properties (Reference Kokhanovsky and MackeKokhanovsky and Macke, 1997; Reference KokhanovskyKokhanovsky, 2004), but there have been few attempts to determine their values reported in the literature. Reference LiboisLibois and others (2013) developed an experimental method, based on combined measurements of reflectance and irradiance profiles, to estimate the value of B for snow (such a method cannot provide an estimate of g G). They find that B varies significantly from one snowpack to another and is generally larger than the value for spheres, B = 1: 25 (Reference Kokhanovsky and ZegeKokhanovsky and Zege, 2004). They argue that underestimating B in snow optical models results in an overestimation of irradiance e-folding depth of the same order of magnitude. In such cases, solar radiation absorbed at depth is overestimated, while radiation absorbed in the upper part of the snowpack is underestimated. This can be critical for the determination of temperature gradients and the consequent snow metamorphism at the very top of the snowpack (Reference ColbeckColbeck, 1989; Reference Sturm and BensonSturm and Benson, 1997). For photochemistry applications, underestimating B leads to an overestimation of the availability of photons at any depth, i.e. an overestimation of the global photochemical activity of the snowpack. The light e-folding depth in snow controls the transmission of shortwave radiation through a seasonal snowpack (Reference PerovichPerovich, 2007) or below snow-covered sea ice (e.g. Reference Nicolaus, Katlein, Maslanik and HendricksNicolaus and others, 2012), which is crucial for photosynthesis and development of life beneath snow or sea ice (Reference Starr and OberbauerStarr and Oberbauer, 2003; Reference ArrigoArrigo and others, 2012). This variety of applications emphasizes the need to accurately estimate B for snow.
This study aims to improve the representation of snow optical properties in common snow models, which treat snow as a disperse granular medium. The objective is to estimate the value of B for a large set of snow samples and to investigate how B is related to snow type and snow physical properties (hereafter ‘sample’ refers to any snow stratum that is homogeneous in grain type or clearly exhibits a dominant grain type). To this end, combined measurements of reflectance and irradiance were performed on an extensive set of 92 snow samples. These comprise homogeneous snow samples measured in the laboratory and stratified snowpacks measured in the French Alps and Antarctica. The value of B is retrieved for each snow sample, following the method described by Reference LiboisLibois and others (2013). However, contrary to Reference LiboisLibois and others (2013) who assume B is uniform in the snowpack, here B is determined for each stratum of a stratified snowpack. This is made possible using an instrument specifically developed to perform irradiance measurements in the snowpack at high vertical resolution. The physical properties of each snow sample are determined in order to investigate the variation of B with snow type, snow density and grain size. A further objective of this paper is to estimate the accuracy of the retrieval method and its sensitivity to measurement errors. This is explored and quantified using Bayesian inference and Markov chain Monte Carlo (MCMC) modeling.
Method
The radiative transfer model TARTES (Reference LiboisLibois and others, 2013) is used, together with density, reflectance and irradiance measurements, to determine B for snow samples prepared in the laboratory, or equivalently for any stratum of a stratified snowpack. First, the theoretical method to determine the optimal B of a sample is presented. Then a stochastic Bayesian framework is used to estimate the impact of measurement errors on the accuracy of the retrieval method.
Determination of B assuming perfect measurements
Reference LiboisLibois and others (2013) introduced a method to retrieve the average B value of a snowpack when the vertical profiles of density, near-infrared reflectance and spectral irradiance are known. This method is questionable when grain shape varies from one stratum to another. Since the present paper is interested in the dependence of B on snow type, it is essential to distinguish snow strata made up of distinct snow types. Hence the method of Reference LiboisLibois and others (2013) is extended to allow B to vary from one stratum to another. The new method is based on the comparison between measured irradiance profiles and irradiance profiles computed with TARTES (Reference LiboisLibois and others, 2013). It provides the vertical profile of B that produces the best match between the measured and modeled profiles. TARTES is a multilayer two-stream radiative transfer model that computes spectral irradiance at any depth in a snowpack where the physical properties and incident irradiance conditions are known. The relevant physical properties are the density, ρ, the specific surface area, SSA (e.g. Reference Domine, Salvatori, Legagneux, Salzano, Fily and CasacchiaDomine and others, 2006), snow grain shape and the amount of light-absorbing impurities (Reference WarrenWarren, 1982); the refractive index of ice is that given by Reference Warren and BrandtWarren and Brandt (2008). In this study, grain shape is represented by the parameters B and g G, and all absorption by light-absorbing impurities is attributed to black carbon (e.g. Reference Sergent, Pougatch, Sudul and BourdellesSergent and others, 1993), the content of which is denoted ‘BC’. According to Reference Bond and BergstromBond and Bergstrom (2006), it is assumed that black carbon has a bulk density of 1800 kg m−3 and complex refractive index m BC = 1: 95–0: 79i. Since the focus of this study is on B, this assumption does not alter the accuracy of the retrieval method. For a natural snowpack, density can be measured manually (e.g. with a cutting device and a scale). In contrast, the quantities B, SSA(1 – g G)and BC are, a priori, unknown. Here they are determined using three independent optical measurements. First, a vertical profile of near-infrared reflectance at wavelength λa provides the vertical profile of the quantity B/ SSA(1 – g G)(from Eqn (1) of Reference Picard, Arnaud, Domine and FilyPicard and others, 2009, and Eqn (15) of Reference LiboisLibois and others, 2013):

where measured a(λa
) is the reflectance at wavelength λa,
γ is the wavelength-dependent ice absorption coefficient and ρ
ice is ice density (917 kg m−3). Irradiance profiles are then measured at two different wavelengths, ![]() and
and ![]() . The algorithm returns the vertical profiles of B and BC that minimize the root-mean-square error (RMSE) between measured and modeled profiles. More details of the method are given by Reference LiboisLibois and others (2013). TARTES is freely available at http://lgge.osug.fr/~picard/tartes/
. The algorithm returns the vertical profiles of B and BC that minimize the root-mean-square error (RMSE) between measured and modeled profiles. More details of the method are given by Reference LiboisLibois and others (2013). TARTES is freely available at http://lgge.osug.fr/~picard/tartes/
Accounting for measurement errors using MCMC modeling
The method presented in the previous subsection provides the profile of B in a snowpack when the measurements are assumed perfectly accurate. In reality, measurements are imperfect and B is a random variable described by its probability density function. Bayesian inference is used to estimate the posterior probability of B given the observations. The standard deviation of B gives an estimate of the retrieval accuracy.
To account for measurement errors, true reflectance, α t(z) true irradiance, I t(z, λ) and true density, ρ t(z), which serve as inputs to TARTES, are now considered random variables. For reflectance measurements, given the characteristics of the reflectance profiler used in this study (Reference ArnaudArnaud and others, 2011), we consider that an error is added to the whole profile, so that the measured reflectance α o(z) is given by
Where ![]() is a Gaussian centered at 0 with standard deviation σα
. For density the error is assumed different for each of the measurements, i.e.
is a Gaussian centered at 0 with standard deviation σα
. For density the error is assumed different for each of the measurements, i.e.
where ρ
o(z) is the measured density profile and ![]() is computed at each level, z. The incident irradiance at the surface of the snowpack,
is computed at each level, z. The incident irradiance at the surface of the snowpack, ![]() (hereafter, bold indicates vectors), is not measured accurately, so it is deduced from exponential extrapolation at z = 0 of irradiance measurements below the surface, and is related to the true incident irradiance at the surface,
(hereafter, bold indicates vectors), is not measured accurately, so it is deduced from exponential extrapolation at z = 0 of irradiance measurements below the surface, and is related to the true incident irradiance at the surface, ![]() , by
, by
Similarly, the logarithm of a single irradiance measurement at depth z, I o (z, λ) is given by
Equivalently, the probability of measuring Io (z, λ) when the true intensity is It (z, λ) is

where
The true and measured irradiance profiles at both wavelengths, ![]() and
and ![]() , and all depths are denoted
I
t and
I
o. We assume that irradiance measurement errors at different depths and different wavelengths are independent, so the probability of measuring
I
o when the true irradiance is
I
t is given by the product of the probabilities given by Eqn (6):
, and all depths are denoted
I
t and
I
o. We assume that irradiance measurement errors at different depths and different wavelengths are independent, so the probability of measuring
I
o when the true irradiance is
I
t is given by the product of the probabilities given by Eqn (6):

Where

and N is the number of irradiance measurements.
Let ω be a state vector that includes the true vertical profiles of density, reflectance, B and black-carbon content, as well as the incident irradiance, ![]() . From these inputs, TARTES computes vertical profiles of irradiance deterministically. Call these modeled profiles
I
f. Assuming that the TARTES model is perfect,
I
f =
I
t and the probability of measuring
I
o for this snowpack is
. From these inputs, TARTES computes vertical profiles of irradiance deterministically. Call these modeled profiles
I
f. Assuming that the TARTES model is perfect,
I
f =
I
t and the probability of measuring
I
o for this snowpack is
P(I o|ω) is usually called the likelihood. The aim of the method is to determine the conditional probability distribution of ω, given the observation, I o, denoted P(ω|I o) and called the posterior probability of ω. To determine P(ω|I o), Bayes’s theorem states that

P(ω) is called the prior probability distribution. All the input parameters are assumed independent, so P(ω) is the product of the prior probabilities of each parameter. Denoting B the vertical profile of B, the marginal posterior probability of B , p(B|I o), is then computed by integration of p(ω|I o).
An adaptive Monte Carlo Metropolis algorithm (Reference Haario, Saksman and TamminenHaario and others, 2001) is used to approximate the posterior distribution, p(ω|I
o) (Reference Patil, Huard and FonnesbeckPatil and others, 2010). It requires the prior probability, p(ω), and the likelihood, p(I
o/ω), given here by Eqn (8). The prior distributions of B and BC in each stratum are assumed uniform in 0.1–3.0 and 0–1000 ng g−1, respectively, which is consistent with the theoretical range of B (Reference LiboisLibois and others, 2013) and the experimental range of BC (e.g. Reference Flanner, Zender, Randerson and RaschFlanner and others, 2007). The prior distribution of ![]() is centered on
is centered on ![]() and follows Eqn (4). The prior distributions of α
t
(z) and ρ
t
(z) are assumed Gaussian and correspond to Eqns (2) and (3), σa
and σρ
, depending on the experimental set-up. The Metropolis algorithm is run for 100 000 steps with a burn-in of 5000 steps and a thinning of 100 steps, i.e. only one in every 100 samples is conserved to avoid autocorrelation of the Markov chain (Reference Link and EatonLink and Eaton, 2012). This yields 950 independent samples taken down from the chain (generally the autocorrelation function is nearly 0 at lag 10). The convergence of the stochastic distribution towards p(ω/Iᵒ) is checked with Geweke’s convergence diagnostic (Reference Patil, Huard and FonnesbeckPatil and others, 2010). The algorithm returns the histogram of B for each stratum, which is a good approximation of the posterior probability of any B of the snowpack. Given the length of the Markov chain, the bin size for B is fixed at 0.05. For the sake of simplicity the output of the algorithm is hereafter simply referred to as a probability distribution function, though strictly speaking this is a histogram. The argument of the maximum of the posterior probability is called the maximum-likelihood estimate (MLE). It is the best estimate of B given the observations. The standard deviation of B is denoted σB
and gives an estimate of the accuracy of the method.
and follows Eqn (4). The prior distributions of α
t
(z) and ρ
t
(z) are assumed Gaussian and correspond to Eqns (2) and (3), σa
and σρ
, depending on the experimental set-up. The Metropolis algorithm is run for 100 000 steps with a burn-in of 5000 steps and a thinning of 100 steps, i.e. only one in every 100 samples is conserved to avoid autocorrelation of the Markov chain (Reference Link and EatonLink and Eaton, 2012). This yields 950 independent samples taken down from the chain (generally the autocorrelation function is nearly 0 at lag 10). The convergence of the stochastic distribution towards p(ω/Iᵒ) is checked with Geweke’s convergence diagnostic (Reference Patil, Huard and FonnesbeckPatil and others, 2010). The algorithm returns the histogram of B for each stratum, which is a good approximation of the posterior probability of any B of the snowpack. Given the length of the Markov chain, the bin size for B is fixed at 0.05. For the sake of simplicity the output of the algorithm is hereafter simply referred to as a probability distribution function, though strictly speaking this is a histogram. The argument of the maximum of the posterior probability is called the maximum-likelihood estimate (MLE). It is the best estimate of B given the observations. The standard deviation of B is denoted σB
and gives an estimate of the accuracy of the method.
Evaluation of the retrieval algorithm
Before applying the retrieval method to real snow samples, the algorithm is evaluated on a synthetic snowpack with chosen physical properties. This synthetic snowpack is 0.5 m deep with layers of 1 cm. It has uniform density ρ = 300 kg m 3 and its reflectance at 1310 nm is 0.35 (corresponding to a specific surface area of ~ 15 m2 kg−1) all along the profile. It is made up of three strata of thicknesses 10, 10 and 30 cm, with B = 1: 2, 1: 7 and 1.3 and BC = 10, 30 and 20 ng g−1. It is illuminated by direct incident light at nadir, with I t surf = 1 W m−2 mm−1. Irradiance profiles at 5 mm resolution over the topmost 30 cm of the snowpack are computed using TARTES. We evaluate the ability of the algorithm to retrieve the vector B for this snowpack.
First, a synthetic set of measurements is obtained by adding random noise to the true density and irradiance profiles according to Eqns (3) and (5), with σρ
= 15 kg m−3 and σI
= 0: 08 W m−2 μm−1. The synthetic reflectance profile is taken as the true profile, otherwise it would introduce some unnecessary bias into the retrieval. The method is applied to this synthetic set of measurements, with λα = 1310 nm, ![]() = 620 nm,
= 620 nm, ![]() = 720 nm, σ
surf = 0: 5 W m−2 μm−1 and σa
= 0: 015, which correspond to typical experimental errors. Only measurements in the top 30 cm of the snowpack are considered, to be consistent with irradiance measurements, which are usually not taken deeper. The Monte Carlo algorithm returns the distribution of B for each stratum. The corresponding histograms and probability density functions are shown in Figure 1. The MLE perfectly matches true
B
, which demonstrates the efficiency of the algorithm. The standard deviation, σB
, of the probability density function depends on the accuracy of the measurements. Here σB
is in the range 0.067–0.082, which corresponds roughly to the accuracy of the method.
= 720 nm, σ
surf = 0: 5 W m−2 μm−1 and σa
= 0: 015, which correspond to typical experimental errors. Only measurements in the top 30 cm of the snowpack are considered, to be consistent with irradiance measurements, which are usually not taken deeper. The Monte Carlo algorithm returns the distribution of B for each stratum. The corresponding histograms and probability density functions are shown in Figure 1. The MLE perfectly matches true
B
, which demonstrates the efficiency of the algorithm. The standard deviation, σB
, of the probability density function depends on the accuracy of the measurements. Here σB
is in the range 0.067–0.082, which corresponds roughly to the accuracy of the method.
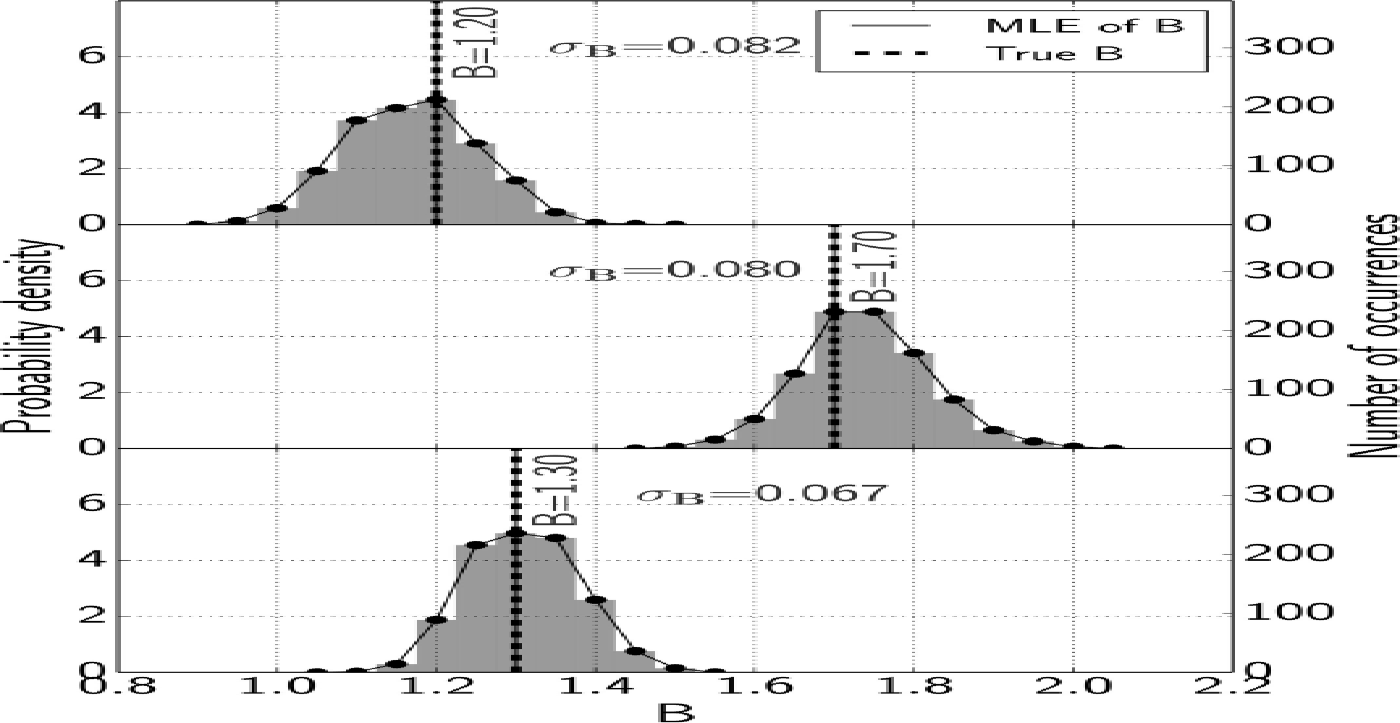
Fig. 1. Histogram and probability density function of B in each of the three distinct strata of the synthetic snowpack. The standard deviation, σB , and maximum-likelihood estimate of each distribution are highlighted.
Materials
The B retrieval method is applied to two sets of measurements obtained under different experimental conditions. The first set was obtained in the laboratory from homogeneous snow samples and the second set was gathered in field experiments performed on stratified snowpacks in Antarctica and the French Alps.
Laboratory experiments
Snow samples were collected at different sites in the French Alps and brought back to the laboratory, where they were stored in a cold room at –20˚C. The samples were taken from strata homogeneous in snow type. To measure the optical properties of the samples, snow was sifted through a 4 mm mesh into a cylindrical sampler (141 mm in diameter and 250 mm long), so that the density was roughly homogeneous. Although sieving generally modifies the micro-structure of natural snow, it was necessary to completely fill the sampler and the sieving had only a small impact for the investigated snow samples, which were mostly isotropic. The inner surface of the sampler is coated with a Duraflect product which has a reflectance exceeding 0.99 in the spectral range 400–1000 nm. From an optical point of view, this configuration is nearly equivalent to a horizontally infinite and homogeneous sample. Reference Bohren and BarkstromBohren and Barkstrom (1974) show that a finite geometry of the cylinder can impact the irradiance profile. They demonstrate that the e-folding depth may be underestimated compared to a semi-infinite slab geometry, larger perturbations occurring at larger e-folding depths. We checked that the e-folding depth has the same spectral dependence as that expected for a semi-infinite snowpack, which ensures that the perturbation due to finite geometry is small in our set-up, probably because the cylinder inner boundaries have very high reflectance. The experimental set-up is depicted in Figure 2. At one extremity, the sample is illuminated by diffuse light generated by a light source coupled to an integrating sphere (diameter 720 mm). Reflected intensity at nadir is measured using a fiber-optic cable placed within the sphere. The cable is plugged into a grating monochromator that measures spectral intensity in the range 400–1000 nm, at 1 nm resolution. Measurements were recorded every 10 nm. Since the bidirectional reflectance of snow is a symmetric function of incident and viewing angles, this set-up is equivalent to measuring the nadir hemispherical reflectance, i.e. the reflectance, , used in TARTES. Calibration curves for the reflectance are deduced from the backscattered intensity measured on reflectance standards with known reflectances of 0.02, 0.20, 0.40, 0.60, 0.80 and 0.99. At the opposite extremity, the sampler is closed by a white plate through which a bare fiber-optic cable (total diameter 8 mm) is inserted into the snow at different distances from the illuminated surface of the sample with an accuracy of ± 2 mm. Irradiance is recorded at various depths and only measurements taken between 2 and 12 cm are used here, because below <2 cm irradiance is not completely diffuse, while >12 cm, with this experimental set-up, irradiance decrease with distance to the surface is not perfectly exponential and the limit of the detector sensitivity is reached. Snow density was measured by weighing the entire sampler. For each sample, photographs were taken with a magnifying lens and snow type was attributed by visual observation. In total, 75 samples were processed, but those for which irradiance did not follow an exponential decay were discarded. They probably correspond either to samples with density inhomogeneities or to samples where the fiber-optic cable position was not sufficiently accurate. Thirty-six samples remained after this selection, for which irradiance was measured at a minimum of four different depths. Irradiance profiles are normalized by the value taken at the surface. More details of the experimental device are given by Reference Sergent, Pougatch, Sudul and BourdellesSergent and others (1993).

Fig. 2. Experimental set-up of the reflectance and irradiance measurements performed in the laboratory.
Density and reflectance are considered uniform in the sample, so TARTES is run on a single numerical layer, 0.25 m thick, with underlying albedo a b = 1 to match the experimental set-up (here the choice of a b has no impact on the retrieved B). The algorithm is run with λa = 950 nm, λ1 I = 620 nm and λ2 I = 720 nm. The estimated accuracy of the reflectance set-up is such that σa = 0: 01. We assume that σρ = 15 kg m−3 (Reference Conger and ClungConger and McClung, 2009) and take σsurf = 0: 2 W m−2 μm−1. We determined σI = 0: 03 W m−2 μm−1 using the residuals of all measured irradiance profiles; σ I includes errors due to the fiber-optic cable position and those intrinsic to the fiber/monochromator coupled system.
Field experiments
The retrieval method was applied to stratified snowpacks at Dome C (75.10˚ S, 123.33° E; 3233 m a.s.l.), Antarctica, and at several sites in the French Alps. A total of 33 sets of measurements were taken in the area of Dome C in the period 28 November 2012 to 14 January 2013. Twenty-four measurements were taken close to Concordia station mainly in the clean area, but with some deliberately downwind of the exhaust fumes of the station. Nine measurements were taken 25 km from the station, where the impact of the station is supposedly much lower. The snowpack essentially consisted of superimposed strata of faceted crystals, faceted rounded grains, rounded small grains and wind-packed snow. Eight measurements were performed in the Alps, at Col de Porte (45.17° N, 5.46° E; 1326 m a.s.l.), Saint Hugues (45.30° N, 5.77° E; 1200 m a.s.l.) and Col du Lautaret (45.04° N, 6.41° E; 2015 m a.s.l.), between 18 February and 24 April 2013. The snowpacks were respectively composed mostly of fresh snow, decomposed and fragmented particles, small rounded grains and large rounded grains.
First, on a flat and horizontal unaltered snow surface, a vertical profile of irradiance was measured with the irradiance profiler SOLar EXtinction in Snow (SOLEXS; Fig. 3). SOLEXS consists of a fiber-optic cable (total diameter 8 mm) that is vertically inserted in the snow into a hole of the same diameter excavated previously. The cable is connected to an Ocean Optics MayaPro spectrophotometer (covering the spectral range 300–1100 nm with 3 nm resolution) and can be displaced continuously in the hole. The light spectrum is recorded every 5 mm, during descent and rise, using a magnetic coding wheel with 1 mm resolution, so that vertical profiles of irradiance are obtained at 5 mm vertical resolution or better, from 350 to 900 nm to ~ 40 cm depth. At deeper sites or larger wavelengths, the signal-to-noise ratio becomes too low because of reduced light intensity, and the shadow of the operator on the setting cannot be neglected. Irradiance profiles are normalized by the value taken closest to the surface. Measuring a single irradiance profile takes ~ 1 min once the setting is deployed. A photosensor placed at the surface records the broadband incident irradiance during the experiment, in order to control the stability of the incident irradiance at the surface. Fluctuations exceeding 3% were discarded. Similar irradiance profilers were used by Reference Warren, Brandt and GrenfellWarren and others (2006) and Reference Light, Grenfell and PerovichLight and others (2008). The main difference is the higher vertical resolution of SOLEXS, which is important for the specific purpose of this study. Once the irradiance measurement is completed, a vertical profile of nadir hemispherical reflectance at λa = 1310 nm is measured at the same place with the reflectance profiler ASSSAP (Alpine Snow Specific Surface Area Profiler, a light version of POSSSUM; Reference ArnaudArnaud and others, 2011). Finally a pit was opened, where the optical measurements were taken. Density was measured at a vertical resolution of 2.5–5 cm, cutting a sample of 250 cm3 and using a 0.1 g precision balance. The snowpack is composed of a superposition of strata. The main strata were identified by visual inspection of grain type in the field, independently of reflectance and density measurements. In general, no more than four distinct strata were observed in the top 40 cm.

Fig. 3. Schematic illustration of the irradiance profiler SOLEXS.
TARTES is run at 1 cm vertical resolution, hence density and reflectance profiles are linearly interpolated on a 1 cm vertical grid. B and the amount of black carbon, BC, are assumed homogeneous within each stratum identified visually, but different strata do not necessarily have the same B and BC. Only measurements taken at 2–30 cm depth were retained. In TARTES, the numerical snowpack is 1 m deep, which is sufficient to consider the medium as semi-infinite in the wavelength range considered. The snow characteristics are taken from the measurements between 0 and 0.3 m. Below, we consider a homogeneous layer with properties of the last measured layer and α
b = 1. The assumed value of α
b has no impact on the retrieved B value. For the irradiance measurements we use ![]() = 620nm and
= 620nm and ![]() = 720nm. The quality evaluation of ASSSAP gives σa
= 0: 03 (Reference ArnaudArnaud and others, 2011) and we choose σρ
= 15 kg m−3 and σ
surf = 0: 05 W m−2 μm−1. We deduce σI
= 0: 08 W m−2 μm−1 from the irradiance measurements taken with SOLEXS exhibiting Gaussian noise.
= 720nm. The quality evaluation of ASSSAP gives σa
= 0: 03 (Reference ArnaudArnaud and others, 2011) and we choose σρ
= 15 kg m−3 and σ
surf = 0: 05 W m−2 μm−1. We deduce σI
= 0: 08 W m−2 μm−1 from the irradiance measurements taken with SOLEXS exhibiting Gaussian noise.
Results
We first consider one set of measurements, to illustrate how the probability density function of B for each stratum of a snowpack is estimated. A sensitivity analysis of the retrieval method to measurement errors is also performed. We then obtain the probability density function of B for all snow samples and, finally, we investigate the dependence of B on snow physical characteristics.
B Retrieval: Some Examples And Sensitivity Analysis
The snowpack studied at Dome C on 14 January 2013 is used as a case study to illustrate the determination of the probability density function of B. This snowpack was composed of three distinct strata. The top stratum was composed of faceted rounded grains (70%) and small rounded particles (30%), while the intermediate and bottom strata were composed of faceted grains, larger in the bottom layer. The measured vertical profiles of reflectance, density and irradiance are shown in Figure 4a and b, where the strata are separated by horizontal lines. The retrieval algorithm is run for this snowpack, from 2 to 29 cm depth. The MCMC is initialized with the state vector that minimizes the RMSE between modeled and measured irradiance profiles (the corresponding profile is shown in Fig. 4b). The distribution of B for each stratum is shown in Figure 4c, along with the corresponding probability density functions. The MLE and the standard deviation of the distributions are highlighted. The standard deviation is larger for the relatively thin top and bottom strata. This shows that the retrieval is less accurate there, probably because there are not enough irradiance measurements within these strata to effectively constrain the retrieval algorithm.

Fig. 4. (a) Measured profiles of density and reflectance at 1310 nm for Dome C measurements taken on 14 January 2013. The horizontal lines delimit the three snow strata. (b) Measured and modeled optimal irradiance profiles at λ I = 620 and 720 nm. Irradiance profiles obtained for identical incident irradiance, but B = 1: 25 (the value for spheres) for all strata are also shown, to highlight the sensitivity of irradiance profiles to B. (c) Histogram and probability density function of B in each of the three strata. The standard deviation, σB , and maximum likelihood estimate are indicated.
The accuracy of the algorithm determines the ability to distinguish between two snow samples in terms of B. This is illustrated in Figure 5, which shows the probability density functions of B for three samples. Each sample corresponds to a 40 cm thick stratum. The measurements were taken at three different locations separated by a few tens of meters at Col du Lautaret, on 18 April 2013 (these measurements are not used in the general analysis). The strata were visually similar, isothermal at 0°C and composed of wet large rounded grains. The overall series of measurements was performed in ~ 1 hour. The probability density functions ensure that B in the two samples corresponding to the shaded curves are different (the probability that both B are equal is 0.007). By contrast, B in the intermediate sample is not significantly different from either of the other two. It is thus possible to distinguish between two samples with B = 1: 4 and 1.7, which gives a low estimate of the accuracy of the method.
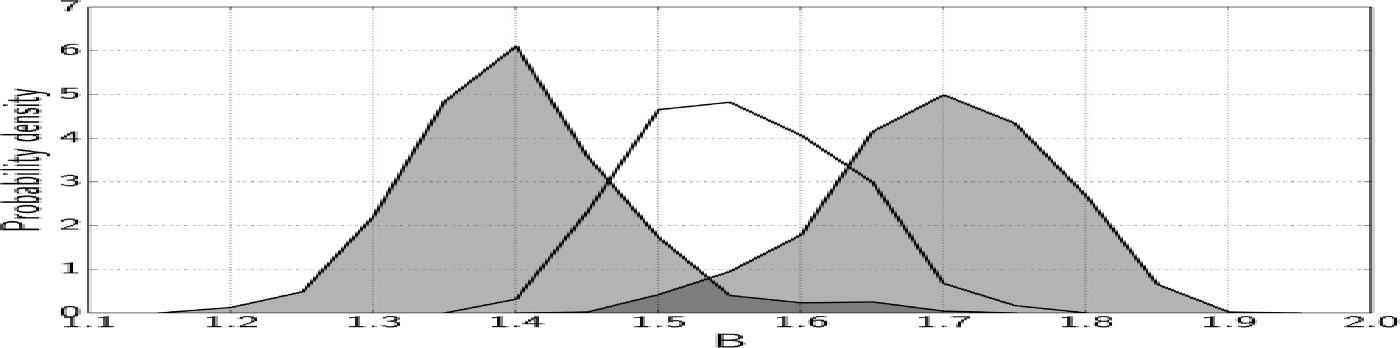
Fig. 5. Probability density functions of B for three samples measured at Col du Lautaret on 18 April 2013.
As suggested by Figure 4, stratum thickness seems to impact the accuracy of the retrieval. This is explored in more detail by calculating σB for every sample of the field measurements, whose thicknesses are in the range 1–28 cm. Figure 6 shows the variation of σB as a function of stratum thickness. σB is also calculated for the intermediate stratum of the synthetic snowpack used for the algorithm evaluation, with this stratum thickness varying from 1 to 28 cm. The variation of σB with stratum thickness for this synthetic case is also shown in Figure 6. For the synthetic snowpack, σB decreases sharply with increasing stratum thickness up to ~ 7 cm. For greater thicknesses, σB is nearly constant, and is bounded by the accuracy of the measurements. Although the experimental values are more scattered, the overall values are coherent with those derived from the synthetic case, i.e. the accuracy of retrieval increases with increasing stratum thickness. σB is generally smaller for the field experiments because the vertical resolution of irradiance measurements, using descent and rise measurements, is often better than the 5 mm resolution of the synthetic snowpack. In light of Figure 6, strata with σB > 0. 095 and those <7 cm thick are not considered in our statistical analysis. In total, ~ 40% (36/92) of the field samples are removed. According to these criteria, only the intermediate layer of the snowpack described in Figure 4 is analyzed.
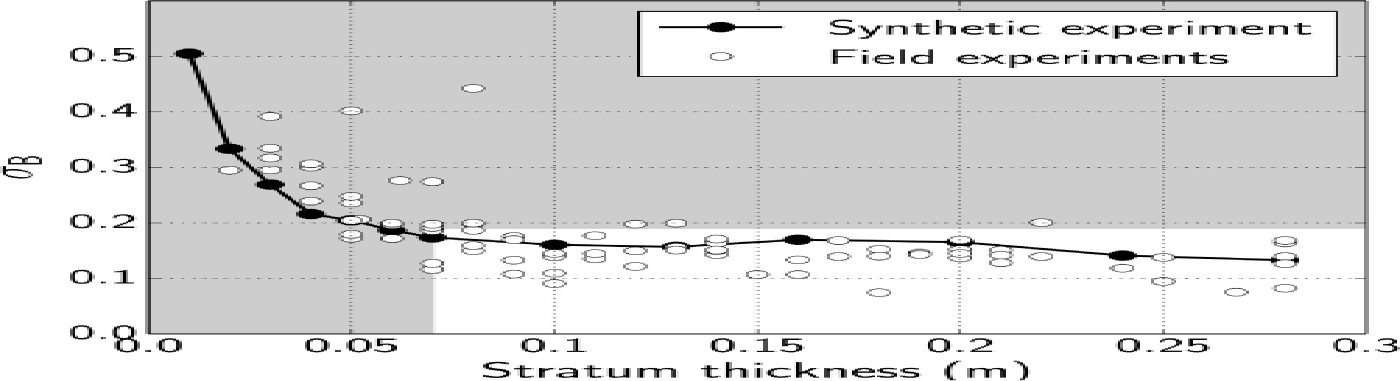
Fig. 6. Standard deviation of B as a function of stratum thickness, for every stratum of the field samples (white circles). Dark circles correspond to the synthetic snowpack. The clear area corresponds to the strata >7 cm thick with σB ≤ 0: 095, retained for the general analysis. Strata in the shaded area are not considered further.
For sufficiently thick strata, the accuracy of the retrieval essentially depends on measurement accuracy. A sensitivity analysis of the retrieval to measurement errors is performed using a synthetic snowpack. To this end, σB is calculated for several sets of measurement errors (σρ, σa, σI ). The sample for which σB is computed has to be sufficiently thick to limit errors due to stratum thickness. For this reason, we use the synthetic snowpack defined previously, except that the strata thicknesses are now 5, 20 and 25 cm. The accuracy indicator is thus the standard deviation of B in the intermediate stratum. For each set of errors, a synthetic set of measurements is obtained, which will depend on the chosen measurement errors. The algorithm is run for this set of measurements and σB is computed. A reference set of errors is chosen (σI = 0: 08 W m−2 μm–1, σρ = 15 kg m−3, σa = 0: 015). Then, to estimate the impact of errors in density measurement, σB is calculated for σρ varying from 0.1 to 10 times its reference value, all other things being equal. The same procedure is performed for the reflectance and irradiance measurements. Figure 7 summarizes the variations of σB with changes in measurement errors. It shows that the accuracy of the retrieval method essentially depends on the accuracy of the irradiance and reflectance measurements, whereas it is almost insensitive to errors in density measurements.
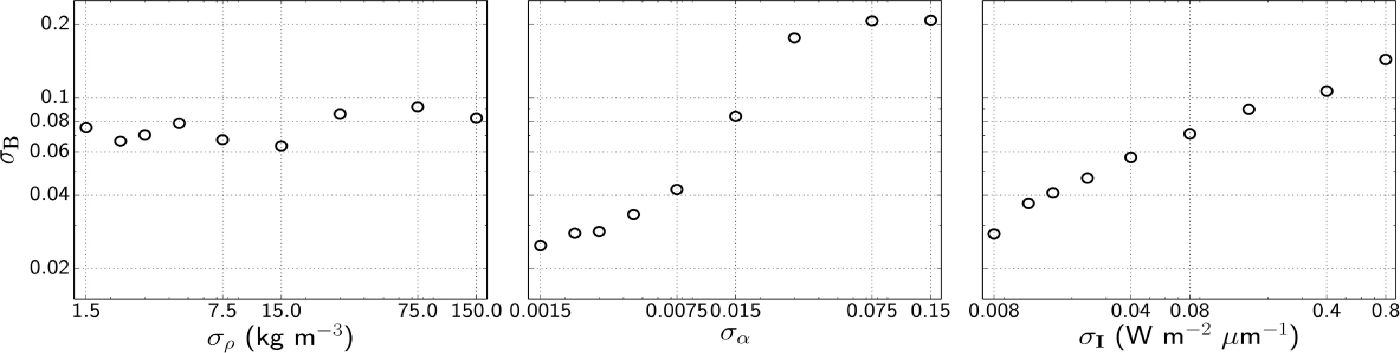
Fig. 7. Variations of the standard deviation of B for the 20 cm thick intermediate layer of the synthetic snowpack, for various measurement errors. The reference state is σρ = 15 kg m−3, σa = 0: 015, σI = 0: 08 W m−2 μm−1. For each graph, measurement errors which are not varied are kept at their reference value.
Probability density function of B for all samples
Following the procedure detailed above, the probability density function of B is obtained for the 56 previously selected field samples and the 36 laboratory samples. The probability density function of B for all these samples is shown in Figure 8. The probability density functions for the different sets of measurements are also shown. First, it is worth noting that the total probability density function is zero outside the range 0.7–2.4, which totally excludes values outside this range. The 90% confidence interval, 1.0–1.90, is in good agreement with the theoretical range obtained for idealized geometrical shapes by Reference LiboisLibois and others (2013): 1.25–2.09. The three sets of measurements have qualitatively similar probability density functions, which supports the assumption that sieving had a minor impact on snow optical properties. In particular they are all maximum at 1: 6 ± 0: 05 and are concentrated in the range 1.4–1.8, which excludes the value for spherical grains, 1.25. The distribution for the samples obtained in the field is wider than for laboratory samples, especially towards the lower B values. This can be attributed to the fact that it is more difficult to take measurements and visually determine distinct strata in the field than it is in a cold room. The secondary peak at B = 0. 85 for the Alps samples corresponds to strata composed of melt/freeze crusts with several refrozen percolation paths. The large vertical structures typical of these strata might be inconsistent with the representation of snow as a collection of ice particles. Such large features may reduce the number of scattering events photons encounter in snow and allow light propagation deeper into the snowpack, resulting in a lower B.

Fig. 8. Probability density function of B for all samples. The probability density functions for the laboratory, Dome C and Alps experiments are also shown individually. The vertical dashed bars show the 90% confidence interval.
The mean standard deviation for all field samples is 0.07, which means that, on average, B is retrieved at approximately ± 0.14 with 95% confidence. For the laboratory experiments, the median standard deviation is 0.13. This is mainly due to the limited number of irradiance measurements in the sample, which does not sufficiently constrain the retrieval method. Moreover, reflectance measurements are taken at 950 nm, as opposed to 1310 nm in the field, hence small measurement errors are more critical than in field experiments (eqn (29) of Reference LiboisLibois and others, 2013).
Relations between B and the physical characteristics of the snow
The probability density function of B has been determined for all samples, which allows us to investigate the relations between B and snow physical characteristics. Since B is a shape parameter, it is expected to vary from one snow type to another. For this reason, the samples were separated into seven snow types given by Reference FierzFierz and others (2009): decomposing and fragmented precipitation particles (DF), small rounded particles (RGsr), large rounded particles (RGlr), faceted rounded particles (RGxf), wind-packed (RGwp), clustered rounded grains (MFcl) and faceted crystals (FC). The probability density functions of B for all samples with the same snow type are summed to obtain the probability density function of this snow type, from which the median, the deciles and the quartiles are calculated. These statistics are summarized graphically in Figure 9. The range between the 25% and the 75% quartiles is ~ 0.25, so most groups largely overlap. Only two snow types distinguish themselves from the others: wind-packed snow and clustered rounded grains, characterized by low B values. This might be explained by the shadowing effect (Reference Wiscombe and WarrenWiscombe and Warren, 1980; Reference WarrenWarren, 1982) occurring in these strata with particularly high density. Snow grains are so close to each other that they cannot intercept light with their whole projected area, which is contrary to the dilute-medium assumption used in TARTES and other radiative transfer models (e.g. Reference Wiscombe and WarrenWiscombe and Warren, 1980; Reference KokhanovskyKokhanovsky, 2004). This may also highlight the limits of the isotropic assumption for snow with marked vertical or horizontal structure. In Figure 9, snow types are ordered from recent to older metamorphosed snow, from bottom to top. This representation exhibits a slight tendency for the median B to decrease with metamorphism (though this is not statistically significant). Even considering broader classes of snow types, the differences between the B values are not statistically significant.
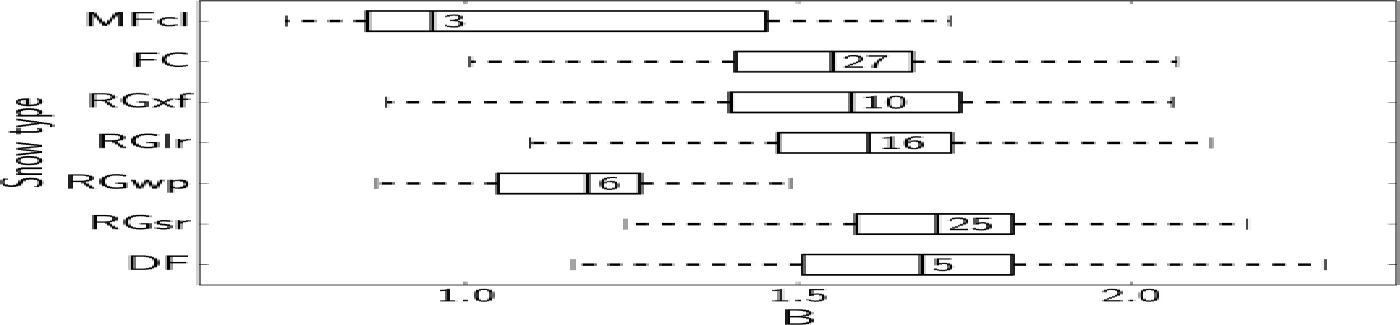
Fig. 9. Box plots of the probability density functions of B for different snow types (MFcl: clustered rounded grains, FC: faceted crystals, RGxf: faceted rounded particles, RGlr: large rounded particles, RGwp: wind-packed, RGsr: small rounded particles, DF: decomposing and fragmented precipitation particles). The central box delimits the first and third quartiles. The dashed lines extend from the first to the ninth deciles. The vertical line within each box indicates the median and the number corresponds to the number of snow samples used for each snow type.
Beyond snow type, the link between B and quantitative snow physical properties is investigated. To this end, the average reflectance and density of each sample are calculated from the vertical profiles. In order to compare the laboratory and field reflectance measurements, which were taken at different wavelengths, they are first converted into specific surface area using Eqn (1). Based on the results of Reference Gallet, Domine, Zender and PicardGallet and others (2009), it is assumed that the scaling constant, B/( 1 – g G), equals the value for spheres, i.e. 5.8. Figure 10 shows the scatter plots of the MLE of B versus specific surface area and density for all samples. The specific surface area varies from 5 to 36 m2 kg−1 and density is in the range 163–510 kg m−3, covering a large range of snow characteristics. There is no correlation between B and snow specific surface area, whatever subset of measurements is considered. There is, however, an overall slight, but statistically significant (at the 95% confidence level), negative correlation between B and snow density (r = – 0.26). The correlation is stronger when subsets of measurements are considered: r = –0.62 for Dome C measurements and r = –0. 49 for laboratory measurements. The dependence on snow density is probably due to the shadowing effect mentioned above.
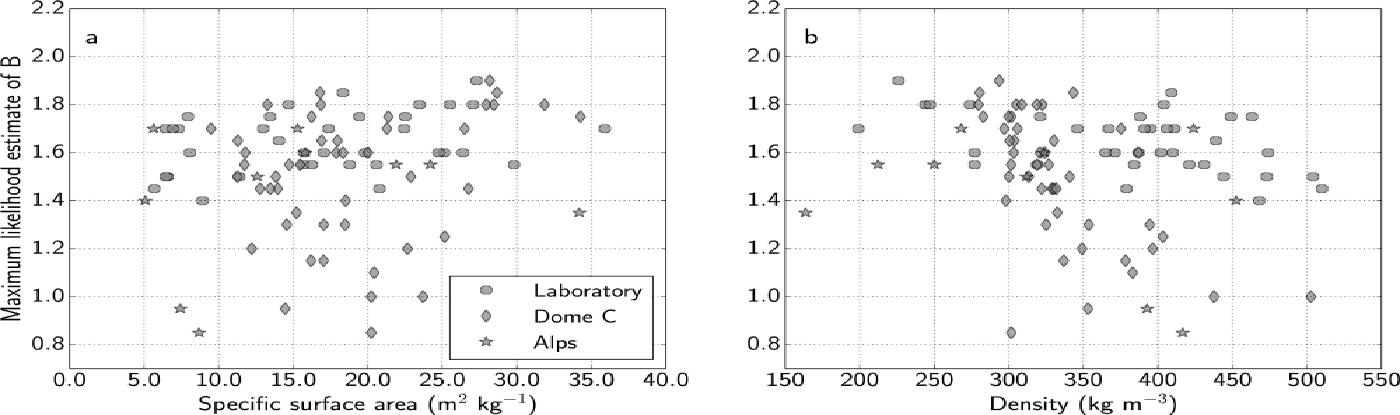
Fig. 10. Maximum likelihood estimate of B as a function of (a) sample average specific surface area and (b) sample average density.
Discussion And Conclusions
Although snow does not look like a collection of distinct particles, that is the most simple and widespread representation in snow optical models. In particular, under the two-stream approximation, a very accurate and widely used approximation in the visible and near-infrared range, snow grain shape can be entirely defined by two parameters: B and g G. The focus of our study has been on the determination of the enhancement factor, B. This parameter is found within 1: 6 ± 0: 2 for most of the 92 snow samples obtained in two different set-ups, which strengthens the validity of the retrieved B. An important result is that these B values are significantly larger than the value corresponding to spheres, B = 1.25. However, grains are assumed spherical in most radiative transfer models of snow, which means that B in snow is ~ 30% larger than assumed in models. This is critical for the light e-folding depth, which depends on B and on the geometric asymmetry factor, g G, of snow grains (Reference LiboisLibois and others, 2013). To first order, e-folding depth computed assuming spherical grains might be overestimated by 30%, on average, since B and (1 – g G) are correlated (Reference LiboisLibois and others, 2013). This is consistent with the conclusions of Reference Sergent, Chevrand, Lafeuille and MarboutySergent and others (1987) and Meirold-Reference Meirold-Mautner and LehningMautner and Lehning (2004), who measured smaller e-folding depths than their models predicted. Since the vertical distribution of absorbed solar radiation within the snowpack is essentially determined by the light e-folding depth, underestimating B by assuming spherical grains tends to drive solar energy deeper into the snowpack. It also tends to smooth temperature profiles in the topmost part of the snowpack, with a potential impact on temperature gradients and snow metamorphism in this region of the snowpack. This apparent limit of the spherical assumption should also be considered for photo-chemistry applications, as well as studies of light transmission through a seasonal snowpack or sea ice. For instance, in a thick uniform snowpack with specific surface area 20 m2 kg−1 and density 300 kg m−3, the actinic flux at 20 cm depth is overestimated by >30% at 550 nm if B = 1: 25 is used instead of B = 1: 6. Likewise, the transmission through a 20 cm thick snow layer with the same characteristics is overestimated by >40% when grains are assumed spherical. These differences increase when snow contains impurities. Finally, studies aimed at distinguishing between the relative contributions of ice and light-absorbing impurities to snow absorption properties (Reference Lee-Taylor and MadronichLee-Taylor and Madronich, 2002; Reference Warren and BrandtWarren and others, 2006; Reference Zege, Katsev, Malinka, Prikhach and PolonskyZege and others, 2008) are very dependent on the assumption made about grain shape. Once the absorption coefficient of snow has been determined, the contributions of ice and impurities have to be separated. Underestimating B leads to an underestimation of the ice contribution to light absorption, and hence to an overestimation of the contribution of impurities (e.g. Eqn (25) of Reference LiboisLibois and others, 2013).
As the parameter B appears essential for several snow applications, it should be given an appropriate value in detailed snow models. Models such as Crocus (Reference Brun, Martin, Simon, Gendre and ColéouBrun and others, 1989; Reference VionnetVionnet and others, 2012) or SNOWPACK (Reference Lehning, Bartelt, Brown, Fierz and SatyawaliLehning and others, 2002) predict the time evolution of snow microstructure (Reference Brun, David, Sudul and BrunotBrun and others, 1992). In these particular models, grain shape is represented by two empirical parameters that evolve with time: the dendricity and the sphericity. Snow type is estimated from the values of these parameters. It is appealing to link these empirical shape parameters to the more physically significant parameter B, so that in snow models optical properties could explicitly depend on grain shape. However, our study shows that B does not vary significantly from one snow type to another, except for the wind-packed and melt forms. At least, the current accuracy of the retrieval method, σ B ≃ 0. 1, does not allow a strict correlation between visual snow type and B. In particular, rounded particles have B values similar to those of faceted crystals, while a value closer to that of spheres might be expected. However, theoretical calculations (Reference Kokhanovsky and MackeKokhanovsky and Macke, 1997) highlight that spheroids have B values closer to hexagonal plates than to spheres. This may be an explanation for the apparent uniformity of the parameter B among all snow types. Although for individual subsets of measurements, density can explain up to 38% of the B variability, this share drops to 7% when all measurements are considered. As explained above, the correlation between B and density is probably more an artifact of the theoretical assumptions used in the model than a physical dependence, so it may be irrelevant for more advanced radiative transfer models. In addition, since B does not seem to depend on specific surface area, no particular evolution of B with snow age is expected. For all these reasons, in optical models based on the Reference Kokhanovsky and ZegeKokhanovsky and Zege (2004) theoretical framework, we simply recommend using a constant B = 1: 6 instead of B = 1.25. For optical models requiring a complete phase function (e.g. DISORT; Reference Stamnes, Tsay, Wiscombe and JayaweeraStamnes and others, 1988), a shape having B = 1.6 should be preferred to spheres. According to table 1 of Reference LiboisLibois and others (2013), B = 1.6 roughly corresponds to the value for spheroids with aspect ratio 0.7, hexagonal plates or cuboids. Accordingly, we recommend using g G so that the ratio B/ (1 – g G) is equal to that of spheres (Reference Gallet, Domine, Zender and PicardGallet and others, 2009). This yields g G = 0.72 or, equivalently, the asymmetry factor g = 0.86. Given that B is found essentially within the range 1.4–1.8, taking B = 1.6 should not induce major errors in snow models. It is worth noting that, despite being a shape parameter by definition, here the retrieved parameter B includes the deficiencies of the granular representation of snow used in our model.
As suggested by the sensitivity analysis of the retrieval method, the latter could be improved by increasing the accuracy of the irradiance and reflectance measurements. It also appears that snow type and density are more easily determined for a homogeneous sample in the laboratory than in the field in a horizontally irregular snowpack. This suggests the development of new laboratory experimental set-ups to estimate accurate B values. Another approach is to determine snow physical and optical properties from snow microstructure obtained with X-ray microtomography (e.g. Reference Kaempfer, Schneebeli and SokratovKaempfer and others, 2005; Reference Haussener, Gergely, Schneebeli and SteinfeldHaussener and others, 2012).
An experimental investigation of the absorption enhancement parameter, B, of snow has been presented. Based on snow optical measurements in the field and in the laboratory and a detailed Bayesian-based analysis method, the present study strongly recommends that spherical grains should not be used to describe natural snow in optical models. This recommendation especially holds when e-folding depth estimation or the profile of irradiance are critical. In models representing snow as a disperse collection of particles, any shape with an absorption enhancement parameter, B, of 1.6 ± 0.2 should be used instead of spheres, except for clustered rounded grains and wind-packed snow, for which the values 1.2 and 1.0, respectively, are more appropriate.
Author Contribution Statement
Q. Libois wrote the manuscript, designed the retrieval method, contributed to the development of SOLEXS and performed the field measurements. G. Picard developed SOLEXS, designed the retrieval method and helped to write the paper. M. Dumont helped to write the paper and contributed to field measurements. L. Arnaud developed SOLEXS and participated in field measurements. C. Sergent, E. Pougatch and M. Sudul performed the laboratory measurements. D. Vial processed the laboratory measurements.
Acknowledgements
This study was supported by the ANR MONISNOW programme. We are grateful to the French Polar Institute (IPEV) for logistic support at Concordia station in Antarctica through the CALVA-Neige programme. The CIBLE programme of the French region Rhones-Alpes (RA0000R457) contributed to the experimental setting.











