Introduction
The altitude at which glaciers exist varies with position (latitude and longitude) and with local factors such as slope aspect (azimuth). Understanding the patterns of such variations provides climatic inferences from both present and past glacier distributions. It is well known that glacier mass balance varies with slope aspect, in ways that differ between regional climates (Reference EvansEvans, 1977; Reference OlyphantOlyphant, 1985). This affects the altitudes, specifically firn line or equilibriumline altitude (ELA), which normally have a minimum value at a single preferred aspect, and a maximum on opposite slopes.
Aspect effects are not large. Their separation from other effects and ‘noise’ requires a precise methodology. The aims of this paper are to provide this methodology, to measure local variation more precisely for different mountain ranges and to account for this variation. This leads to a model for the variation of north–south altitude contrasts with latitude.
A methodology is developed here that uses periodic (circular, harmonic, Fourier) regression of altitude on the cosine and sine of accumulation area aspect. The regression makes full use of the data available and provides measures of the strength of local contrasts between northward and southward slopes (for the cosine) and between eastward and westward slopes (for the sine). Separating these two components of asymmetry is useful as only the north-south contrast reflects radiation and shade effects. To focus on local (mesoclimatic) effects of slope aspect and gradient, it is best to allow for regional trends in glacier altitude (e.g. by including further terms in latitude and longitude in the regression). Such trends have been used previously to infer regional wind directions and precipitation trends (Reference Østrem, Haakensen and ErikssonØstrem and others, 1981). Here it is shown that analysis of variations with aspect may permit further inferences about cloudiness, a component of palaeoclimate about which little other evidence is available.
In the face of larger factors affecting glacier altitude, and of noisy data, reliable estimation of these coefficients requires large datasets. Fortunately these are available for much of the world in the World Glacier Inventory (WGI) (Reference Müller and ScherlerMüller and Scherler, 1980; Reference Haeberli, Bösch, Scherler, Østrem and WallénHaeberli and others, 1989, Reference Haeberli, Hoelzle and Suter1998). Although this constrains the analysis in that the definitions used are not necessarily optimal for a study of mesoclimatic effects, the WGI does provide information on glacier size, type, relief, location, altitude and aspect. This permits some causal factors to be investigated.
All WGI data available in digital form on the internet have been analyzed in this way. With further data for Greenland and Nepal, they cover over 66 000 local glaciers with altitude and aspect data. Figure 1 shows the world distribution of the 51 glacier regions analyzed.
Hypotheses: aspect effects on glacier balance
Reduced ablation leads to a more positive local mass balance on shadier, poleward-facing slopes. Therefore the north–south contrast should be of greater magnitude for steeper glaciers, for higher relief, for sunnier climates and further away from the Equator and the Poles. It may also be greater for mountain, cirque or niche glaciers than for large valley glaciers or ice caps. Shade and radiation incidence should give no asymmetry at the Poles and Equator.
The east–west contrast reflects wind effects on drifting and heat transfer, and morning/afternoon differences in temperature and cloudiness (Reference EvansEvans, 1977). It may be greater where relief is lower, and where westerly or easterly wind components are stronger. Effective winds are those which drift snow during and just after snow-bearing storms, and those during the melt season, whose turbulence increases heat transfer to windward slopes while those to the leeward are sheltered. Northerly or southerly winds may weaken or strengthen the north–south contrast, so the separation of incident radiation and wind effects cannot be exact. Airflow cooled by glaciers reduces heat transfer in leeward regions, reducing ablation and giving a self-preservative effect which may lower ELA on larger glaciers.
Alternative causes of asymmetry are considered to be mainly of local significance (Reference EvansEvans, 1977). Topography with strong structural lineation may displace the modal glacier aspect but is unlikely to affect glacier altitudes over large areas. The regions analyzed here have ridges in various orientations, providing sites for glacier development on all aspects. Thus results for these extensive regions reflect essentially climatic controls of mass balance. Hence the consistency of north–south contrasts.
Structure of the paper
The availability of data affects and constrains the possible analyses, so the data are first considered in terms of the WGI variables used, their spatial coverage and their editing. The use of mid-altitude is justified and the application of Fourier regression to aspect data is explained. Results are given for north–south contrasts for major regions and sub-regions, for east–west contrasts and for the effects of individual glacier gradients on north–south contrasts. A further analysis accounts for variations in the degree of north–south asymmetry between regions. Application to former glaciers is followed by conclusions on methods and on glacial asymmetry.
Data
The WGI was planned during the International Hydrological Decade (1970s). It was completed for mainland Europe and the USSR (mainly in the 1970s), and later for New Zealand, but for only parts of the Americas, China and the Himalaya (Reference Haeberli, Hoelzle and SuterHaeberli and others, 1998). Data are now freely available on the internet from the US National Snow and Ice Data Center (NSIDC, 1999, updated 2005), and some were previously received from the World Glacier Monitoring Service at Zürich, Switzerland. The WGI is organized by country, and then by drainage basin. Some deficiencies of existing Inventory data are noted below, but it remains the only broad basis for the study of glacier distribution and glacier change, and its use continues (e.g. in Reference BahrBahr, 1997).
Variables
For almost all glaciers, the WGI provides accumulation and ablation area aspects, highest and lowest altitudes (elevations), area, location as latitude and longitude, and classification by several criteria. Aspects are given, unfortunately, only to eight compass points. Length is given for many glaciers, but other variables such as snowline and true mean altitude are given only for a minority. Where ‘snowline’ (firn line) is given, as in Soviet and Chinese data, it is most often an estimate rather than a measurement, and the method used varies. Data for gradient are not given explicitly, but can be estimated overall by relating length to height range, the difference between highest and lowest altitude.
A second dataset is available from NSIDC: the Glacier Inventory of West Greenland (Reference Weidick, Böggild and KnudsenWeidick and others, 1992), providing 3550 further local glaciers, mainly in the temperate zone (they range from 59.85 to 71.03° N). Although this is a simplified version of the WGI, it does give latitude, longitude, area, maximum and minimum altitude and six classifications. Thus it is possible to exclude ice-sheet outlets, ice caps and icefields. Aspect was given for ablation area only (as also for Bolivia in the WGI), but it was used here as there is usually a strong circular correlation between this and accumulation area aspect. (For New Zealand, accumulation and ablation area aspects are identical for 57% of glaciers longer than 1 km, and for 93% of shorter glaciers.)
Finally, data were also taken from the International Centre for Integrated Mountain Development (ICIMOD) Glacier Inventory of Nepal (Reference Mool, Bajracharya and JoshiMool and others, 2001). The most useful results were obtained by dividing Nepal into four regions.
Coverage
The WGI internet data with aspect and altitudes analyzed here (Fig. 1) cover 30 370 local glaciers in central and northern mainland Asia, 8611 in mainland Europe including the Caucasus, 13 870 in western North America, 1612 in the tropical Andes, 851 in Chile, 2777 in New Zealand and 1285 in the Arctic north of 70° N. With the further 3550 in southwest Greenland and 3158 in the Himalaya (3089 in Nepal and 69 in the WGI for Nanga Parbat) the 51 regions providing regression results include 66 084 local glaciers. A further ten regions have 611 local glaciers with aspect data, but either lack altitude data or do not provide significant or plausible regressions. The huge Tien Shan–Pamir–Dzhun-gar–Karlik system, with 24 579 glaciers in the WGI, was subdivided into 11 regions (among the 20 in Figure 2. Note that ‘eastern Tien Shan’ (et) is defined here as the Narat and Terliskay ranges, from 82 to 87° E. Range names are given in anglicized form, as succinctly as possible.

Fig. 2. Distribution of region centroids in central Asia, showing divisions of the Tien Shan and adjacent systems used in the present analysis. The two-letter region abbreviations are given in Table 3.
Most available glaciers are in middle latitudes, between 37 and 53° N. The complete absence of data between 17 and 33° S, and between 0 and 27° N, is especially unfortunate. As there are glaciers at these latitudes in the Andes, these are gaps in current digital coverage rather than in glacier distribution. The data are incomplete for North and South America, and absent or inadequate for southwest Asia, Tibet and much of the Himalaya. Only a small proportion of Canadian and Alaskan glaciers are included in the on-line data, and there are none for the Rocky Mountain system. Data for Antarctica, Mongolia (with 180 glaciers on the east side of the Altai and in several small ranges) and Iceland are not available. Data for China include the Altai, Tien Shan and intervening ranges, and the Qilian Shan, but as yet exclude the Chinese Pamir and Tibet (Kun Lun, Altyn Tagh, Himalaya and other ranges) for which editing continues in Lanzhou. Comparison with Reference Wang and YangWang and Yang (1992) shows that the 12 367 Chinese glaciers available are only 27.3% of the total, covering 19.6% of the estimated Chinese glacier area.
Data editing
Data for each glacier inventory were subjected to consistency checks as a result of which a number of corrections were made. Errors were found in altitude, position and occasionally aspect and length data, mainly by checking outlying points on scatter plots (Evans and Cox, unpublished information). The quality of data varies from excellent to poor, generally being better for the data most recently edited and placed on the internet. Despite clear WGI guidelines, countries used glacier classifications differently and applied different policies on the inclusion or exclusion of rock glaciers, glacierets, ice patches and ‘glacier groups’. Rock glaciers are excluded here, except where glacier classification is unavailable.
Gradient modulates the effects of slope aspect. This potential control is calculated as the arctangent of height difference/length. As length is not necessarily measured from highest point to lowest point, gradients thus calculated from the WGI should be regarded as approximations. The steepest gradient found on detailed maps of the Alps was 57°, for a hanging glacier on the Chamonix Aiguilles, France. The numerous gradients calculated to be more than 45° were thus viewed with suspicion, especially for glaciers not classified as hanging. As many were small (100 or 200 m long), the fact that length is recorded to the nearest 100 m causes important rounding errors. Hence, for glaciers steeper than 45°, length was increased by 50 m, and gradient was recalculated. Although arbitrary, this correction for rounding moves these high gradients in the more likely direction.
Overall, few individual corrections were needed to the Soviet Union and northern China dataset, already edited in Moscow or Lanzhou and by Reference Bedford and HaggertyBedford and Haggerty (1996), or to the New Zealand dataset. However, consideration of initial results for wind-affected Siberian ranges such as the Urals, Putorana, east Sayan and Kodar showed a surprising westward tendency, contrary to the eastward tendency noted in the literature (e.g. Reference DolgushinDolgushin, 1961; Reference KrenkeKrenke, 1982) and calculated from printed Soviet Glacier Inventories by Reference EvansEvans (1977). It eventually became clear that east and west had been inverted for the Soviet and Chinese data. The appropriate mirror-image correction was made (e.g. northwest was converted to northeast). Further checks by NSIDC revealed that Soviet data for three medium-sized areas (drainage basins) had been omitted from the 1996 dataset; these were incorporated into the Pamir, Dzhungar and Altai regions.
Methods
Mid-altitude as a surrogate for ELA
Glacier altitude can be related to climate at both local and regional scales. The response of most interest is ‘balance ELA’, the average altitude at which net accumulation on the glacier surface above is balanced by net ablation below. Unfortunately, this is available for few glaciers in the WGI because it requires detailed observations over a number of years, relating annual ELA to annual net mass balance so that the ELA yielding zero net balance can be interpolated. Reference Osmaston, Peel, Chisholm and HaggettOsmaston (1975) reviewed several possibilities for estimating ELA. Estimates based on full hypsometry and assumed accumulation-area ratio (AAR) values are not widely available. For the great majority of glaciers in mountain regions, debris cover and type of accumulation (avalanche, wind-drifting, rime) also complicate ELA estimates from present inventory data (Reference Benn and LehmkuhlBenn and Lehmkuhl, 2000).
A surrogate that is broadly available is required. Among the few variables available for almost all WGI glaciers are highest and lowest altitudes, i.e. the heights above sea level of the top and the snout of each glacier. As Reference Kaser and OsmastonKaser and Osmaston (2002, p.44) exemplify, the higher above the ELA a mid-latitude glacier starts, the lower below the ELA its snout extends. Thus a representative value for the altitude of each glacier is obtained by averaging the highest and lowest altitudes, giving the mid-range altitude or middle altitude, abbreviated to mid-altitude.
Reference Müller, Caflisch and MüllerMüller and others (1976, p. 169) estimated ELA for 484 Swiss glaciers and found a close relation to mid-altitude (r = +0.945) which, in turn, correlates (r = +0.957) with median altitude. (Here r is the Pearson product–moment correlation, used here for simple bivariate relations.) These correlations are as strong as can be expected given measurement errors. Some further support comes from correlations of mid-altitude with mean altitude (Kurowski’s method: Reference Osmaston, Peel, Chisholm and HaggettOsmaston, 1975), and with air-photo-based estimates of snowline, for the large Eurasian WGI datasets here. These correlations range between r = +0.82 and +0.999. Reference Cogley and McIntyreCogley and McIntyre (2003) recommend use of mid-altitude in preference to the contour-curvature firn-line method of Hess. Further, they find the mid-altitude to be very close to the ELA for 37 glaciers studied for mass balance. Both they and Reference Leonard and FountainLeonard and Fountain (2003) find that mid-altitude estimates ELA more precisely (lower rms error) than does Hess’s method. This confirms the utility of using glacier midaltitude as the response variable in the present study. Distances of 40% and 45% up-glacier from the ‘toe’ (snout) to the headwall have been used to estimate ELA in palaeoglaciological studies (Reference Benn and LehmkuhlBenn and Lehmkuhl, 2000), but varying the definition of mid-altitude away from 50% hardly changes the results given here. It must be accepted that any generally applicable method gives considerable scatter in ELA estimates. Thus mid-altitude is an acceptable surrogate for firn line and ELA.
Fourier regression
Earlier quantitative work on glacial asymmetry used vector analysis to summarize the numbers of glaciers with accumulation areas facing different aspects (Reference Evans and ChorleyEvans 1969, 1977). Given a unimodal distribution with a single favoured aspect, the resultant vector provided both a vector mean (the best estimate of the favoured aspect) and a vector strength measuring the extent of deviation from a uniform distribution across aspects. This method provided good summaries of asymmetry in areas of marginal glaciation, but could not express asymmetry in mountain ranges such as Mont Blanc where most ridges are high enough to generate glaciers on all slopes, even though ELA still varies between aspects. Comparison between favoured directions given by vector analysis and by regression are made by Reference EvansEvans (in press).
Fourier (harmonic) regression (Reference BlissBliss, 1970, ch. 17; Reference FisherFisher, 1993; Reference WilksWilks, 1995, ch. 8.4;Reference BloomfieldBloomfield, 2000) can provide a flexible, complementary tool, measuring asymmetry by relating altitude (or size, or other quantitative variables) to aspect. Fourier regression on the circle is the most obvious approach given the requirement for identical predictions for both 0° and 360°. The fitted curve should be smooth and differentiable throughout, and unaffected by the arbitrary choice of origin on the circle. The first Fourier term (first harmonic) fits a cosine curve and a sine curve to a full cycle (360°), permitting a single minimum altitude that can be at any aspect. This is appropriate for measuring any of the climatic effects discussed above. Further terms permitting more complex curves proved unnecessary for the present data and hypotheses. The first Fourier term can alternatively be expressed as a sine (or a cosine) curve with a displacement (phase), but the version with both cosine and sine permits the desired separation of north–south and east–west contrasts. Given glacier accumulation area aspect θ, latitude φ and longitude λ, mid-altitude, A m, is modelled as
where b 3 and b 4 allow for a spatial trend within a region, linear in latitude and longitude. The coefficients of greatest interest are b 1 and b 2, measuring the two components (north–south and east–west) of asymmetry.
As a smooth curve is fitted to all available data, regression results are more reliable than averages for sectors of aspect (‘mean north’ cf. ‘mean south’), especially where some sectors may have few data. The first Fourier term provides a simple unimodal model that lends itself to climatic interpretation. The cosine of azimuth has a maximum of +1 at 0° (north) and a minimum of −1 at 180° (south). Hence its coefficient (bļ) predicts the value (here, altitude in metres) for north compared with the predicted average for east and west. As south deviates by the same amount, in the opposite direction, doubling b 1 measures north–south altitude contrast directly in metres. The sine of azimuth has a maximum of +1 at 90° (east) and a minimum of −1 at 270° (west). Hence its coefficient (b2) predicts the value for east compared with the average for north and south: double this measures east–west altitude contrast.
As an example, Figure 3 a shows the altitudes of 2777 glaciers in the South Island, New Zealand (Reference ChinnChinn, 2001), in vertical histograms for each aspect. Also plotted is a line giving predictions from the first Fourier regression (Table 1, equation 1). Data for aspect 0° are repeated at 360° so that the full curve can be considered more effectively. Despite the low proportion of variance accounted for (R2), only 0.096, the variation of altitude with aspect is highly significant (p < 0.001). Unless otherwise stated, significance is taken to mean a significance level below 0.05. Such tests, including confidence intervals, depend on the assumption that values for each glacier are independent of those for other glaciers. The R2 values are adjusted downward throughout this paper to allow for the number of fitted constants and the number of observations. This has little effect for large datasets.
Table 1. Three regressions for mid-range altitude, A m (m) for 2777 glaciers in South Island, New Zealand; φ is latitude, λ is longitude and θ is glacier accumulation-area aspect
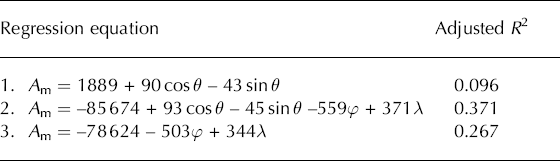

Fig. 3. First-order Fourier regressions for South Island New Zealand glaciers. Using the same vertical scale, (a) plots data for midaltitude against aspect, and (b) plots values predicted from the four-control equation (aspect and position). The curves give predictions from aspect alone, from Table 1, equation 1. The vertical variation for each aspect, shown by the histograms, gives in (a) the actual within-aspect variation due to position and other factors, and in (b) the variation accounted for by the linear trend in latitude and longitude in Table 1, equation 2. Bins are 20 m wide and, to complete the circle, data at 0° are repeated at 360°.
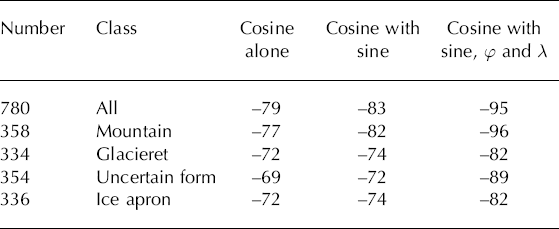
Stability of cosine coefficients
Coefficients for the cosine term in a single-control regression are very similar to those where both sine and cosine are included. Table 2 exemplifies this for the Washington Cascades, USA, a medium-size dataset. Often, however, the sine term is insignificant at the 0.05 level, because the lowest altitude is for an aspect close to poleward. Generally, insignificant terms are dropped from a regression and it is recalculated without them. However, being orthogonal over the whole circle, the two components of the first Fourier term are a special case and should be taken together as yoked terms; for comparability between areas, it is undesirable to drop either the cosine term or the sine term, even when one is insignificant. (Both Reference JeffreysJeffreys (1983, p. 343) and Reference Helsel and HirschHelsel and Hirsch (1992, p. 342) provide strong support for retaining both terms.) It is logical to permit lowest altitude to be at any aspect, including those close to cardinal points of the compass.
Table 2. Stability of cosine coefficients (b 1 (m)) for mid-range altitude, Washington Cascades, for one-, two- and four-control equations. (φ is latitude, λ is longitude)
Note that the possibility exists that, even where the regression is significant, both coefficients can be insignificant. This instability of coefficients arises because of collinearity between the actual cosines and sines. Sine and cosine functions are orthogonal over the circle, and so uncorrelated, but small datasets for Putorana, east Sayan and Kuznetsk Alatau are limited to part of the circle (90° for Putorana), over which cosine and sine show substantial correlation. All three, in western Siberia, produced highly insignificant regression results but are too widely separated to be amalgamated.
Strangely, there are two further regions, the polar and subpolar Urals, and Armenia, where the results are plausible despite the regression and coefficients being insignificant. In all five regions the range of observed aspects is 180° or less. As these results are unreliable and narrowly based, the five regressions are not included in the present analyses.
Most regions analyzed here are sufficiently large that they contain a linear trend in glacier altitude. This relates mainly to precipitation variation, and accounts for more variability than does aspect. The effect is included as linear terms in latitude and longitude. In general, glaciers are higher in the centre of a massif, but such trends at several scales are complex and variable, and require detailed studies of each region. The effects of glacier type, size and gradient also vary considerably, sometimes because glaciers have been classified differently. Thus considerable scatter due to these effects is not accounted for here.
Figure 3b shows the effect of allowing for linear trend in New Zealand, where glaciers are regionally higher to the southeast, after exclusion of the North Island (with only 18 glaciers). Mid-altitudes predicted from position and aspect (Table 1, equation 2) are plotted for each glacier. Variation within each aspect is thus due to the spatial trend. The outlying points at the top are in the Spenser Mountains, well to the north of the other glaciers. Table 1 shows that in this case, similar aspect coefficients are obtained whether or not latitude and longitude are included in the regression. The regressions on latitude and longitude are obviously applicable only within the South Island. The R2 values in Table 1 show that the effects of aspect and position (equations 1 and 3) are approximately additive (0.267 + 0.096 ¼ 0.363, cf. 0.371 for the combined equation). Hence coefficients change only a little. All terms in these three equations are highly significant.
Allowing for spatial trends sometimes has more effect on the cosine coefficient, b 1, either weakening or (as in the Washington Cascades (Table 2)) strengthening this measure of north–south difference. This interaction arises where some aspects are concentrated in one part of the region, as in Stikine, adding a positional component to differences due to aspect. In this case, Fourier coefficients from regressions including locational terms are to be preferred. These are therefore used here generally, to facilitate comparisons.
Table 2 also shows that similar b 1 coefficients are obtained for different glacier types. Such results are typical, and show that these controls are sufficiently weakly correlated for coefficients to be stable. Addition of further possible controls to the equation causes only minor changes. The R 2 values for the 780-glacier regressions are R 2 ¼ 0.04 for the cosine;0.06 when the sine is added;0.27 with latitude and longitude; and 0.40 when height difference is included as a fifth control (then b1 = −93 m).
To provide comparable results then, the results below are for coefficients from four-control multiple regressions, of mid-altitude on cos θ, sin θ, latitude and longitude. An exception is made for Nanga Parbat, where the midpoints of glaciers range over only 19 km × 20 km and implausibly high latitude and longitude coefficients were obtained, implying a trend of 35 m km−1. This reflects local rather than regional differences, and it is best to use the simpler Fourier regression on aspect alone for such small regions.
The increased variability in glacier altitude as study areas are extended makes R 2 a poor measure for comparing regions of different sizes. Thus the emphasis below is on regression coefficients and rms error, rather than R 2.
Results
Figure 4 compares Fourier curves of the variation in midaltitude for broad groupings of Eurasian mid-latitude ranges. It emphasizes the strong north–south asymmetry of the Alps, and of the five central Asian regions except for the western Tien Shan. Aspect variation there and in the Caucasus shows a small eastward displacement of the minimum midaltitude. This effect is greater in the Altai and is attributed to westerly winds.

Fig. 4. Fourier curves for variation in glacier mid-altitude with aspect for broad groupings of middle-latitude Eurasian mountains. Each is based on up to five of the regions in Table 3. The aspect effect from a combined regression on aspect, latitude and longitude is added to observed mean altitude in each broad region.
Fourier regression results are discussed here initially for north–south contrasts in middle-latitude mountain ranges. Numerical values of cosine coefficient b 1 and related variables for each region are given in Table 3.
Table 3. Cosine and sine coefficients (b 1, b 2) of Fourier regressions for mid-altitude, A m (including within-region trends on latitude and longitude, φ and λ), plus the means of possible explanatory variables, and abbreviations used in figures, for 51 regions ordered by latitude. Here d is height difference (range of altitude), g is gradient, ϕ is latitude, λ is longitude and Abb is abbreviated name

North–south contrasts
Figure 5a is a plot of b 3 for the mid-latitude glaciers. Results show a large difference between the north–south asymmetry of mid-altitude for glaciers in coastal maritime climates (Scandinavia, Vancouver Island, the Olympics and Patagonia, all humid and on west coasts), and those in continental interiors. In central Asia the north–south contrast (twice b 1) rises eastward to 304 m in the central Tien Shan (around Pik Pobedy and the Kyrgyz–Chinese border) and to greater values for the ranges around Ürümqi: the Dzhungar, Iren Horu, Bogdo and Karlik ranges, surrounded by desert. Both the (Tajik) Pamir and the Qilian Shan are very dry mountains, with continental, mainly cold glaciers at the highest altitudes of all the extratropical regions analyzed. Not surprisingly, north-facing glaciers average 318 m (for the Pamir) and 348 m (for the Qilian Shan), lower than southfacing glaciers. Within the Pamir, 1200 niche glaciers are steeper (mean 30°) and higher (4968 m) than other forms, and have an even greater coefficient of −246 ± 27 m, where ± indicates 95% confidence limits.

Fig. 5. Confidence intervals for coefficients from Fourier regressions including latitude and longitude trends. (a) Absolute cosine coefficients for glacier regions in middle latitudes (all have lowest glaciers on poleward aspects). (b) Cosine coefficients in low and high latitudes. All five tropical regions have lower southward- (and thus poleward-) facing glaciers: three arctic regions have lower glaciers facing equatorward, but significantly so only for Wrangel I. (c) Sine coefficients significantly different from 0 at the 0.05 level: westward components are on the left and either very weak or in tropical regions; eastward are on the right.
In Chile, at around 34° S, southeast of Santiago, there is a degree of asymmetry at least comparable to the Pamir and Qilian, although there are also effects of westerly winds. Nanga Parbat’s cosine coefficient of –264 m (a 528 m north– south contrast) is the highest found, and almost an outlier. Although this small dataset cannot be ignored, the 95% confidence limits are broad: from −167 to −360 m. The relief on Nanga Parbat is among the highest on Earth, so a strong radiation incidence effect is unsurprising. Nevertheless it is probably overstated by this coefficient. Data are available also for mean altitude, giving a coefficient of −159 ± 99 m which is comparable to the Qilian and Ürumqi region results. Snowline altitudes give an even smaller coefficient, −120 ± 71 m, and both indicate a more eastward tendency. For this small dataset, intercorrelations between mid-range, mean and snowline altitudes are unusually weak.
The Cascades, Pyrenees, Alps and Caucasus are intermediate: they have wet and dry sub-regions, as do the Alay and northwest Tien Shan, the Altai and New Zealand. The Altai cosine coefficient is −88 ± 15.8 m (i.e. north–south contrast of 176 m), which is compatible with the average north–south contrast of 202 m found by Reference Klinge and LehmkuhlKlinge and others (2003) for a dataset of 2036 glaciers, including western Mongolia. New Zealand (South Island) gives a moderate cosine coefficient of 93 ± 10 m. The Nepal regions and south Yukon also have intermediate cosine coefficient values.
There is a large difference between Scandinavia and the rest of Eurasia. Most of Scandinavia is so maritime and cloudy that north–south asymmetry is limited, although significant. In northeast Russia, north–south contrasts are moderate both in the extremely continental Suntar-Khayata and Chersk ranges, and in the Koryak range beside the Bering Sea. The latter show less maritime influence than does the Kamchatka Peninsula, further south. In three cases in Figure 5a, and four in Figure 5b, 95% confidence intervals overlap zero. As low asymmetry is expected in some cases, and the intervals here are not as broad as for the five regions excluded above, these regions are retained in further analysis.
Axel Heiberg and Ellesmere Island indicate weak north-directed asymmetry. Coefficients for three arctic regions (Svalbard, Novaya Zemlya and especially Wrangel Island) show lower south-facing glaciers (Fig. 5b; Table 3) despite removal of overall trend. This must reflect factors other than radiation contrasts, probably the southerly source of moisture in the Arctic. Coefficients for Peru and Bolivia show significant southward (that is, poleward) asymmetry.
North–south contrasts for subdivisons
The smallest datasets included in Figure 5 and Table 3 are for the Kodar and Saur ranges, with 30 and 34 glaciers, respectively, but with highly significant regression results. Both are sufficiently isolated to discourage their being merged with neighbours. Hence it is reasonable to consider further subdivision of some of the ranges with thousands of glaciers.
The Alps were divided at the Great St Bernard, San Bernardino and Brenner Passes. Taking the 2343 ‘normal’ glaciers, b 1 for the whole Alps is −103 ± 12 m. For the four major divisions, the coefficient strengthened from −87 m for the wetter west, through −118 m for both central divisions, to −124 m in the sunnier east. However, confidence intervals are overlapping at ±17 to ±21 m. Coefficients for the four divisions of all 5025 glaciers and glacierets varied less regularly: −94, −130, −109 and −118 m, with confidence intervals between ±13 and ±18 m, so the contrasts are marginal.
Asymmetry is greater in the northeast and southern Altai than in the windward northwest and central Altai. Dichotomy of the Tajik Pamir at 72.5° E produced the expected eastward increase in radiation asymmetry, with a significant difference between the west with b1 = −124 ± 14 m and the east with b1 = −164± 15 m (but an insignificant difference if position is ignored). Differences between northern half and southern half and between northwestern half and southeastern half were less. The value of b1 is greatest in the north (−280 ± 33 m for 612 glaciers north of 39.2° N, essentially the Za-alay range), probably because of higher relief: it is lower in the Pamir’s western and eastern fringes, because of wetter climate and lower relief respectively.
The large Stikine dataset was divided into seven regions. North–south asymmetry was low in the Coast Mountains around the lower Stikine, north of 56.9° N (b1 = −52 ± 17 m); greater around the lower Iskut (b1 = −109 ± 15 m) and Mess Creek (Edziza Range and western Skeena Mountains: b1 = −80± 13 m); and low again in the East Skeena Mountains (b1 = −40± 10 m) and interior Stikine Plateau, probably because relief there is lower. The rain shadow effect of the Coast Mountains is weaker here than in southern British Columbia.
In the Brooks Range of northern Alaska, where moisture comes from the southwest, north–south asymmetry is greatest in the east (which also has higher, longer and steeper glaciers): b 1 = −68±24 m for the 350 glaciers there, but contrasts are insignificant in the central and western divisions. For the Brooks Range overall, inclusion of latitude and longitude makes b 1 = −41 ± 22 m, compared with b 1 = −118 ± 33 m without the trend, an unusually large difference. The 597 Brooks mountain glaciers give b 1 = −46 ± 28 m and for the 140 glacierets b 1 = −67 ± 57 m.
North–south asymmetry is greater also in the less maritime climate of northern Sweden than in northern Norway. In New Zealand, dividing the South Island into nine regions by lines of longitude, b 1 coefficients were 89–109 m for the five main regions between 167.6° E (Lake Te Anau) and 170.5° E (Lake Tekapo), and confidence limits included the b 1 value of 93.4± 9.7 m for the whole Island. Weaker asymmetry is found to the north and in Fjordland, both with lower relief. As all glaciers are in a narrow belt near the main divide, it was not possible to separate the effects of drier eastern from wetter western climates. Elsewhere, although subdivision of major regions produced some broad confidence intervals, it generally showed variations of asymmetry with relief and wetness.
East–west contrasts
Sine coefficients, b 2, in middle latitudes are often an order of magnitude less than cosine coefficients (Table 3), and exceed them only in South Norway. This shows that the effects of the diurnal march of temperature and cloudiness, although widespread, are minor compared with those of solar radiation incidence and shade. Sine coefficients are important or significant (Fig. 5c) only where wind effects are particularly strong, in parts of the west wind belt with moderate mountain relief. In the Altai and its neighbour the Saur, east-facing glaciers are some 110m lower than westfacing ones, compared with differences of 90m in South Norway and New Zealand’s South Island, 130m in the Washington Cascades and 300m in north-central Chile (N.C. Chile), the extreme case (Fig. 5c).
The Caucasus, the Alps, the Dzhungar and Iren Horu, all exposed to the west, have an eastward component that is significant but much smaller than the northward. Likewise in the Tien Shan and Pamir, there is a small but significant eastward tendency (glacier altitude is lower facing north-northeast) in the windward ranges, i.e. the southwest Tien Shan (Turkestan and Hissar Ranges), the Alay and the Pamir (Fig. 5c). Elsewhere south of 43° N (Almaty), the whole Tien Shan system has small and insignificant sine coefficients, as do the Bogdo and Karlik Ranges east of Urumqi. (Note that the sign of b 2 had to be reversed following the inversion of eastward and westward noted earlier for the Soviet and Chinese data. Results taken directly from the on-line ‘Eurasia’ dataset, 1996–2004, would differ in sign.)
Although maps of surface winds in Eurasia show outward movement from the Siberian winter anticyclone, mountain winds at altitudes of glacial accumulation (500 and 700 hPa levels) are more consistently westerly, and at all seasons almost all storm tracks between 30° N and the Arctic progress from west to east.
Kamchatka, with a Pacific moisture source, has westfacing glaciers nearly 120 m below east-facing, and the lowest glaciers are on northwest aspects (318°). Although the coefficients for Kamchatka are not quite significant at the 0.05 level, the preferred aspect agrees with 334° for the significant vector resultant of glacier numbers. In the Arctic, local asymmetry is very different, with definite eastward components in Novaya Zemlya, Svalbard and Wrangel Island. The same three regions have positive cosine coefficients, showing lower south-facing glaciers.
In Canada, there is a small but significant eastward component in Stikine and south Yukon, as in the Brooks Range. In Nepal, only the northwest division has a significant eastward component. In the tropics, Peru and Bolivia show westward tendencies rather weaker than the poleward. Convective afternoon cloud in the tropics protects west-facing glaciers from ablation to some extent, and east winds may shift some snow to leeward.
Gradient effects
The hypothesis that radiation and shade effects should be greater for steeper glaciers can be tested where glacier length is given in addition to height difference and aspect. The best test is where large numbers of glaciers permit narrow classes of glacier gradient to be analyzed, without giving broad confidence limits on Fourier coefficients. Thus for the 19 188 glaciers of the Tien Shan–Pamir system, 5° classes could be used. Note that, logically, zero gradient is associated with zero cosine coefficient.
All regions show an increase in asymmetry with gradient (Fig. 6). The increase is steepest (and around fourfold) for the sunniest regions, Iren Horu in Xinjiang west of Ürümqi, and Qilian (IH and Ql in Fig. 2). Except in New Zealand, where a steady but gentle increase is exhibited, the asymmetry increase with increasing gradient flattens out, and sometimes reverses, at the steepest gradients. Analysis of the largest dataset, Tien Shan–Pamir, gives a very clear result. The increase in asymmetry with gradient levels out once the gradient is over 30°, where the 4455 glaciers have a cosine coefficient of −204 m. For the 866 glaciers with gradients lower than 10°, the cosine coefficient is −61 m, while for the 13 867 between 10 and 30° it is −141 m. All these coefficients are from regressions on aspect (sine and cosine), latitude and longitude.

Fig. 6. Cosine coefficients with 95% confidence intervals, for gradient bands within five regions, and Tien Shan-Pamir which combines eight regions from east Tien to southwest Tien. The latter has 19 188 glaciers and was therefore divided into 5° gradient bands. Overlapping 10° bands were used for the other five regions: top and bottom classes are open-ended. Coefficients are plotted against mean gradient for each band.
In the Iren Horu and European Alps too, north–south differences level out at gradients above 30°. There is, however, a contrast between the northernmost region plotted, the Altai around 50° N where the trend is weakest and asymmetry slightly declines above 25°, and the most equatorward, the Qilian at 39° N, where it levels only at 35°. This supports the idea of a latitude-dependent threshold.
Other areas cannot be so finely subdivided, and it is inappropriate to combine those in contrasting climatic regimes. Data for the California Sierra Nevada (442 glaciers), the Washington Cascades (715), the Brooks Range (876), North and South Scandinavia (1967) and even West Greenland (3550 local glaciers) give broad, overlapping confidence intervals for 10° classes of gradient, with little apparent gradient effect. Cosine coefficients for Greenland do peak around 30° (b 1 = −141 ±57 m for 28–33°), and those for Scandinavia at 20–25° (b 1 = —79 ± 33 m). Glacier latitudes in both regions average 65° N.
Instantaneous north–south contrasts in direct clear-sky solar radiation incidence are expected to increase with gradient almost linearly, up to gradients equal to the solar elevation angle. Beyond that, pole-facing slopes are in shade and there is little further increase in absolute contrast. Solar elevation outside the tropics varies between zero and (113.5° – latitude) at midday in mid-summer, when the sun is directly overhead at the Tropic (23.5°). Maximum solar elevation is thus 73.5, 63.5 or 53.5°, respectively at latitudes 40, 50 or 60°. The average, integrated over daytime in the ablation season, is considerably less and it is not surprising that in most regions gradients beyond 30° fail to increase contrasts. The gentler trends for New Zealand, the Alps and the Altai are attributable to climates cloudier than in the three central Asian areas in Figure 6. The contrast between the Qilian results and those for the Altai, Greenland and Scandinavia suggests that at higher latitudes asymmetry peaks on lower gradients, but further data are needed to test this.
Degree of North–South Asymmetry: Further Analysis
Given the paucity of information about climate in high mountain areas, especially those with glaciers, the presence of glaciers themselves has to provide evidence of climate. Using information calculable from the WGI itself, the following can be used as surrogate explanatory variables for |b 1|, the degree of north–south (poleward) asymmetry in a given region:
Mean height difference between highest and lowest points on each glacier provides a relevant measure of relief;
Mean gradient, calculable where length as well as altitude information is given, affects radiation received on a given aspect;
Mean length, alternatively the mean square root of area, expresses the possible ‘self-preservative’ effect of larger glaciers (Reference TronovTronov, 1961) in cooling surface air;
Means of middle, highest and lowest altitudes themselves relate to the climate experienced by glaciers, especially through altitudinal effects on air density, radiation, humidity, precipitation, cloudiness and temperature;
Mean latitude and longitude summarize the position of the group of glaciers, with further effects on regional climate.
All these potential controlling factors were calculated for the 51 regions tabulated in Table 3, averaging some 1200 glaciers per region. However, it must be remembered that the number of glaciers varies from 30 for the Kodar Range in Siberia to 7865 for the Stikine–Iskut region of British Columbia. Thus the support for each result varies considerably unless analyses are weighted by the number of glaciers. Before calculating correlations and multiple regressions, it is necessary to take the absolute values of mean latitude and of b 1, to allow for the two hemispheric regions. Thus the absolute cosine coefficient gives the contrast in altitude between equatorward and poleward aspects (it is taken as negative for the three arctic regions with ‘inverted’ asymmetry).
In an initial analysis of the 37 regions between 34° and 70° latitude, the most robust effect on north–south asymmetry was that of altitude. This is because of its direct effects on climate and because, for a given latitude and relief, glaciers are higher where the climate is drier (so that lower temperatures compensate for lower snowfall). The regression of the absolute value of b 1 on altitude, weighted by numbers of glaciers, is thus:
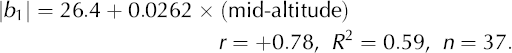
Hence for mid-altitude = 4000 m, a coefficient of ±131m is expected, which is reasonable. Other weighted correlations for |b 1| over these 37 temperate and low-arctic regions are r = −0.69 for absolute latitude and 0.65 for height difference. Inclusion of height difference as a second control with altitude increases R 2 to 0.62, but its individual contribution is not significant. Without weighting, R 2 for this relationship is slightly higher, but only because of Nanga Parbat, a region with the highest values of both |b 1| and mean height difference (1468 m; the next highest is 686 m), and with only 69 glaciers it is unduly influential.
Over all 51 regions, mean highest and mean lowest altitudes correlate (r = +0.999) with mean mid-altitude, so only the latter is considered here. Correlations around −0.88 between glacier altitudes and absolute latitude make separation of these effects difficult. Also mid-altitude correlates (+0.62) with height difference, so the controls are not additive. Simple correlations with |b 11 are considerably increased by weighting by the number of glaciers per region. The strongest correlation is then r = +0.64 with midaltitude (Fig. 7). The relation is strong except for the five tropical regions (Bo–Ec; bottom right, with the three Peruvian regions plotting between) and Nepal (n1 and n4), where the monsoon climate may reduce asymmetry. This is followed by +0.51 with height difference, −0.56 with the square of latitude and −0.47 with absolute latitude itself. These last two are combined in the quadratic models of Table 4.
Table 4. Models for variation of north–south asymmetry, |b i|, over 51 regions. Weighting is by number of glaciers per region (sum of weights is 66 084): φ is absolute mean latitude (i.e. N or S) and α is mean mid-altitude, per region. Power models are fitted by non-linear least squares. Unweighted results are included to show that coefficients are not greatly changed by weighting: the final models in (a) and in (b) are those preferred. Note that the standard deviation of |b 1| is 58.9 m, reduced to 45.3 m after weighting. Because the overall variances differ, R 2 values are not comparable before and after weighting: rmse (rms error) values are comparable, and give the better comparisons between models


Fig. 7. North–south glacier altitude asymmetry (cosine coefficient) as a function of mid-altitude. The two-letter region abbreviations are given in Table 3.
Mean gradient correlates (r = +0.41) with |b 1|, but also (+0.45) with mean mid-altitude, for the 49 regions available (length being unreliable for Stikine and Yukon). Mean length has weaker correlations. The altitude effect on |b 1| is dominant, and gradient and height difference do not add significantly to it. Also, mean height difference reflects glacier size as well as topographic relief (hence at the regional scale the correlation between mean height difference and mean glacier gradient is only +0.15), and mean height difference is therefore a poor surrogate for topographic relief.
The effect of latitude is clear once the (small number of) arctic and tropical regions are included. The relation to absolute latitude (i.e. treating both North and South latitudes as positive) shows greatest north–south asymmetry in middle latitudes. Asymmetry related to shade and radiation incidence (neglecting diurnal cloudiness variations) should be zero at the Equator and the Poles. A quadratic model does not do this automatically. A customized model is preferable.
A model based on the sine and cosine of latitude seems natural. When they are multiplied together, the result is zero at both 0 and 90°. Hence we propose sine–cosine power models, both symmetric and asymmetric, fitted here by nonlinear least squares. All predictions are positive. Table 4a compares the results with those from quadratic and linear models. The symmetric model raises the product of sine and cosine of absolute latitude to a single power, and thus constrains the maximum to be at 45°. Weighting has only a small effect on the predictions, and Figure 8 shows only the weighted fits. The symmetric model consistently underpredicts tropical asymmetry, and over-predicts arctic asymmetry. The asymmetric model achieves a worthwhile improvement in rms error by fitting separate powers to sine and cosine, permitting the latitude of maximum asymmetry to vary. The curve now comes closer to the five tropical results. The weighted version achieves rms error of 33.7 m in estimating the absolute cosine coefficient.

Fig. 8. North–south glacier altitude asymmetry as a function of latitude. Non-linear least-squares fits are shown for symmetric (dashed) and asymmetric (solid line) sine–cosine power functions. Fits are weighted by number of glaciers (n) per region, and the symbols therefore distinguish three sizes of region.
Differentiation of the sine–cosine power equation gives the latitude of greatest north–south asymmetry as arctan√(sine coeff./cosine coeff.)). Converted to degrees, this is latitude 36°. This displacement from 45° is expected because of the aridity of the sub-tropics, permitting glaciers only at high altitudes where asymmetry is greatest.
A somewhat closer fit is obtained by adding a term for mean mid-altitude. The improvement is small but significant. The simple relation to altitude (Fig. 7) is linear if latitudes below 34° are excluded. Asymmetry varies with altitude mainly in (northern) middle latitudes, where glaciers are regionally higher in arid and sunny continental interiors. As this is where the largest datasets are found (Fig. 8), weighting for glacier number permits altitude to give a closer prediction, with rms error only 35.2 m (Table 4b). Combination with quadratic latitude reduces this to 30.3 m. The sine–cosine power model improves on this to give rmse 29.6 m, for four fitted constants. Figure 9 compares these predictions with the actual values of |b 1|. Nepal, the Caucasus and most Tien Shan divisions plot below the line, as do Scandinavia and arctic regions, while asymmetry in north-central Chile, West Greenland (north) and the Koryak ranges is under-predicted. The extreme values for Nanga Parbat and Wrangel Island are based on small numbers, as discussed above. The scatter is not surprising given the use of surrogate variables, and in part must be due to data limitations.
Neither height difference, gradient nor length adds significantly to the quadratic or sine–cosine power combined models in Table 4b.
Note that the coefficient for mid-altitude here (0.0270) is close to that in the simple regression above for the 37 mid-latitude regions (0.0262). Although overlapping and competing for the same predictive space, both latitude and altitude are consistent and important controls.
It is best to conclude that north–south asymmetry varies with both altitude and latitude. For a given latitude, mean glacier altitude reflects variation in aridity and seasonal differences (continentality). Temperature contrasts between northward and southward slopes increase with altitude as lower air density and humidity reduce sensible- and latent-heat transfer, and radiation becomes relatively more important. The effect of latitude is geometric, through solar elevation angle and its diurnal and seasonal cycles, and the related variations in atmospheric solar path length. Further geometric controls (gradient, height difference and length) from the available data do not improve estimation of asymmetry.
Application to Former Glaciers and to Cirques
Glacial cirque floor altitudes may relate to former ELAs, and have been used to interpret former climates (mainly temperature and precipitation). Application of Fourier analyses to reconstructed palaeoglaciers, or to cirques, should thus provide further valuable palaeoclimatic information. This goes beyond that provided by former ELAs, as information on the direction and degree of asymmetry (for fixed latitude and relief) relates to sunniness/cloudiness and wind conditions.
Table 5 shows that strong north–south asymmetry is found in the cirques of southwest British Columbia (these two ranges are on the dry side of the Coast Mountains near 50° N; Reference EvansEvans, 1990), but not in England and Wales where the negligible R 2 values and lack of statistical significance (0.69 < p < 0.87) confirm the absence of an aspect effect on cirque floor altitude. The British Columbian results are highly significant (p <0.0001). The value of b 1, with 95% confidence intervals, is −107 ± 39 m for the Cayoosh Range and −95 ± 41 m for the Bendor.
Inclusion of latitude and longitude does not materially affect these regressions. As both regions are in middle latitudes, north–south asymmetry is expected unless conditions are very cloudy. Relief in the English and Welsh mountains is low, but sufficient to provide slope contrasts. There is thus a strong implication that palaeoclimate in Britain was very cloudy during the main phases of cirque formation. Such palaeoclimates were, however, relatively sunny in these ranges of southwest British Columbia. In both regions, cirques were developed at stages intermediate between ice-sheet glaciation and non-glacial conditions. The study of asymmetry thus adds to our knowledge of palaeoclimate, taking it beyond that from changes in overall ELA. Where large datasets of cirques or former glaciers can be analyzed, Fourier regression provides information on cloudiness that has previously been unavailable.
Conclusions
Methods and general
For large datasets, the Fourier coefficients are shown to be a reliable way of comparing the effects of aspect on glacier mid-altitude. The first cosine coefficient is usually stable in relation to the addition of sine and other terms to regressions for glacier mid-altitude. The main limitations are that most of the circle should be included in data values, and asymmetry needs to be strong to achieve statistical significance at conventional levels, even in a dataset of 200. It is best to allow for latitude and longitude trends affecting glacier midaltitude, mainly windward to leeward, especially over large areas. Where data for mean or median altitude, firn line or ELA are available, results are consistent with those for midaltitude, the data most widely available. Despite several limitations, current WGI data provide valuable information on glacier size, altitude and aspect.
Glacier altitude and aspect
North–south differences are weak in the tropics and the Arctic, and in maritime climates such as Scandinavia, Vancouver Island and the Olympic Mountains. They are stronger in dry continental climates such as the Pamir, Xinjiang east of Ürümqi, and Qilian Shan, where ELAs are high for the latitude. Cosine coefficients (b1) are mainly below ±60m in maritime climates and above ±150m in continental climates. Coefficients are high in ranges with high relief where glacier overall gradients are high, such as Nanga Parbat. The effect of increasing gradient was clear within regions, especially in central Asia, but between regions it was masked by the correlation of mean gradient with mean altitude. North–south contrasts are maximized for glaciers steeper than 25 or 30°, and quite small for glaciers with gradients less than 10°.
Large east–west differences in glacier altitude are due mainly to winds (westerlies except in Kamchatka). Most sine coefficients (b 2) are below ±50 m, nearly an order of magnitude less than b 1. The largest (Table 3) are −150 m for north central Chile, −87 m for Nanga Parbat, −65 m for the Washington Cascades and −61 m for Wrangel Island. Vector analyses (cf. Reference EvansEvans, 1977) suggest stronger wind effects in the West Siberian plateau and rounded-mountain areas, such as the Urals, Putorana, east Sayan and Kuznetsk Alatau, but for reasons noted above, the calculation of useful Fourier regressions for these was not possible. Westward components of lower altitudes in the tropics are due to afternoon cloudiness or east winds.
By controlling air density and temperature, altitude affects the importance of radiation compared with heat transfer in melting. Thus the effects of radiation on mass balance are greatest at high altitudes as well as at middle latitudes. North–south asymmetry due to shade and solar radiation incidence is general throughout temperate zones, and dominates in the ranges of central Asia and the Alps. It seems that wind is a less important control of local variations in altitude (and of glacier aspect) than is the incidence of solar radiation and shade. Radiation effects on north–south contrasts logically fall to zero both at the Poles and at the Equator. An appropriate model developed here to describe latitudinal variation in the contrasts observed is an asymmetric sine–cosine power function. With the largely Northern Hemisphere data available, this model predicts greatest such contrasts around 36° latitude.
Table 5. Fourier regressions for cirque floor altitudes, A c (m); θ is cirque headwall aspect and n is number of cirques

When applied to palaeoglaciers, or to cirques, Fourier analysis of aspect (azimuthal) effects provides valuable climatic information additional to that from change in ELA. For example, it implies that parts of the British Columbia Coast Mountains were sunny during cirque formation, but England and Wales were much less so. Thus aspect–altitude analysis for former glaciers provides new evidence of cloudiness.
Future Work
The next generation of Glacier Inventories will be more accurate and consistent (Reference Paul, Kääb, Maisch, Kellenberger and HaeberliPaul and others, 2002), with more precise aspect values such as the gradient-weighted vector mean of aspects throughout the accumulation area (Reference Evans and ChorleyEvans, 1969). Improved estimates of ELA may become more widely available, taking account of the factors and problems discussed by Reference Benn and LehmkuhlBenn and Lehmkuhl (2000). Better topographic data and improved estimates of climatic conditions in high mountains should permit explanation of a greater proportion of variance in glacier altitude. At present, in high mountains ‘climate measurements are rare and ...geo-ecological environments provide detailed information about climate patterns’ (Reference Klinge and LehmkuhlKlinge and others 2003, p. 296). At a given latitude, glacier altitudes suggest spatial patterns of precipitation.
Acknowledgements
We thank A. Glazovskiy for information on the Soviet Glacier Inventory, G.K.C. Clarke for further Yukon data, T. Chinn for further New Zealand data and P.K. Mool for the Nepal data. Many others responded helpfully to data queries. Valuable discussions were held with M.A. Church on statistics, and M. Maisch and F. Paul on the WGI. A. Long, W. Mitchell, E.J. Klok and R. Naruse (Scientific Editor) instigated useful improvements and clarifications. For the WGI data we thank M. Hoelzle and W. Haeberli and NSIDC at Boulder, CO (National Snow and Ice Data Center, 1999, updated 2005).

















