Introduction
The evolution of a glacier subject to a surface mass balance has traditionally been computed using a kinematic boundary problem, and a model geometry that is updated at each time-step. The evolution of the boundary is usually given by

where s = s(x, y, t) is the surface elevation, vi the velocity in the directions i = x, y, z and bsurf the surface mass-balance function in the vertical (z) direction. Another formulation of the boundary evolution is based on the conservation of mass (Reference Picasso, Rappaz, Reist, Funk and BlatterPicasso and others, 2004)
with h = h(x, y, t) the ice thickness and vi the depth-averaged components of the horizontal velocity.
The boundary described by s or h is a function of x and y; that is, for every (x, y) there is one and only one corresponding boundary. No vertical front or overhanging part can be described. The surface (in the xy-plane) covered by the glacier must be known a priori (which is no trivial task in the case of advancing or retreating glaciers). If the computational domain exceeds the domain covered by the glacier, there exists an (x, y) without an associated boundary. For this reason, the surface covered by the glacier should be determined before solving the kinematic boundary problem (e.g. Reference Picasso, Rappaz, Reist, Funk and BlatterPicasso and others, 2004). For vertical fronts, no ablation can be prescribed, since the surface mass-balance function is defined vertically. Computation of topological changes such as breaking or merging (e.g. separation of one retreating glacier into two smaller ones, failure of the frontal part of a hanging glacier, unification of two growing glaciers) is not a straightforward process.
To overcome these difficulties, we propose a continuum approach which treats the glacier surrounded by air as one computational domain composed of two regions (ice and air) with distinct material properties. The motion of the ice-air interface in the computational domain is described on the basis of a level-set method (Reference SethianSethian, 1999; Reference Osher and FedkiwOsher and Fedkiw, 2001). A level-set function <(x, t) localizes the material position, and is defined by ip(x, t) = —1 in the ice and by <(x, t) = 1 in the air, except in the vicinity of the ice-air interface, where a smooth transition of < ensures the continuity of the level-set variable. The interface is defined by <(x, t) = 0. The initial condition of is given by
with d the normal distance to the ice-air interface, negative in ice and positive in air, and S a small value representing the size of the transition of < The spatial and temporal variation of <(x, t) near the interface is governed by the general Hamilton-Jacobi equation
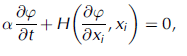
with H the Hamiltonian and i the index of the space dimension. For an initial value formulation of the level-set problem, α = 1 and the Hamiltonian reads (Reference SethianSethian, 1999)

The speed function F, describing the normal velocity of the interface, is positive in the direction of n. The normal direction n is oriented with respect to increasing ’.
The coupling of the level-set method with physical problems is widely used in numerical simulations, especially to describe the behavior of two-phase flows (see Reference SethianSethian (1999) or Reference Osher and FedkiwOsher and Fedkiw (2001) for a review). The adaptation of the level-set method into glaciological terms represents a special mode of the two-phase flow problem, as the behavior of only one phase, i.e. the ice, is significant. The introduction of the second phase (the air) into the computational domain allows us, however, to describe the evolution of the interface using a level-set method.
The level-set method describes a one- or two-dimensional interface with a higher-dimensional function ’(x, t) (two- or three-dimensional). In comparison to a kinematic boundary method, the interface motion is therefore implemented with one additional spatial dimension. The interface is not described as accurately using a level-set method compared with a kinematic boundary formulation, since the localization of the ice–air boundary depends on the discretization of ’ in the vicinity of the interface. However, the use of this higher-dimensional function makes it possible to describe discontinuous elevation profiles or vertical fronts (Reference Pralong, Funk and Lu¨thiPralong and others, 2003). Topological changes in the evolving interface are well defined and are handled naturally (Reference SethianSethian, 1999). The steady-state geometry of a glacier can be evaluated by computing the steady-state form of the level-set problem coupled with the ice–air flow problem. Time integration is therefore not required.
Model
In order to calculate the ice and air motion in the computational domain, the behavior of both fluids has to be modeled and the motion of the ice–air interface defined by means of a speed function. Boundary conditions must also be specified.
Ice and air rheology
The ice is incompressible. Its behavior is described by
with σ the Cauchy stress tensor, p the pressure, δ the Kronecker symbol, 2Ƞ ice the ice viscosity and ε the strain-rate tensor. The viscosity 2Ƞ ice is defined by Glen’s flow law
with A and n the flow parameters (Reference GlenGlen, 1955; Reference SteinemannSteinemann, 1958) and 11ε the second invariant of the strain-rate tensor. While the domain around the glacier corresponds physically to the atmosphere, it does not need to exhibit the rheology of air, simply a rheology which does not influence the motion of the ice. Therefore the airflow law is given by Equation (6), replacing 2Ƞ ice by 2Ƞ air and defining 2Ƞ air = ε2Ƞ ice.ε has to be set as small as possible; a value that is too small generates numerical instability. The air density p air is set at zero. The transition of the viscosity and the density between ice and air is continuous (e.g. Reference Chang, Hou, Merriman and OsherChang and others, 1996):
where 2Ƞ(<) and p(<) express the viscosity and the density over the whole computational domain. Ƞ ice and p ice are related to ice, and Ƞ air and p air to air. Table 1 lists the numerical values of the model parameters.
Table 1. Values of the model parameters for ice of 0°C. A, n, p ice are
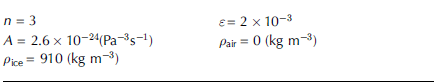
Linear level set
The glacier surface moves simultaneously in two different modes. First, it is passively advected by the velocity field v of the media at the ice–air interface. Expressing only the component of the velocity normal to the surface, the corresponding speed function becomes
where n surf is the normal to the surface, pointing out of the ice. Second, it is influenced by the surface mass-balance vector b surf, which defines the accumulation or ablation at the glacier surface. The speed function is
In the case of vertical accumulation and ablation, the surface mass-balance vector reads
with z the normalized vertical vector and b surf the surface mass-balance function in the vertical direction. The speed function describing the motion of the ice–air interface is the sum of F adv and F mb (Reference SethianSethian, 1999). Since the normal is given by

the global speed function F becomes, in the case of vertical accumulation and ablation,
Introducing F in Equation (5) and the Hamiltonian in Equation (4), the variation of <(x, t) at the ice-air interface is expressed by

This equation describes the temporal evolution of the variable <p in the whole computational domain, i.e. the motion of the ice-air interface (defined by <=0 The interface is convected by the velocity field v and the surface mass balance b surf oriented in the vertical direction. The level-set method will be evaluated and discussed on the basis of this equation.
Non-linear level set
The surface mass-balance vector, as defined by Equation (12), does not depend on the shape of the interface. However, the level-set method allows the surface mass balance to be expressed easily as a function of the slope z n surf, the aspect n surf — (z_n surf)z or the curvature K surf of the interface. K surf is expressed as (Reference SethianSethian, 1999)

Since K surf and n surf depend on < Equation (15) becomes non-linear. It reads

In Equation (15) or (17) the accumulation and ablation are described in the direction of z. In that way, vertical fronts or crevasses cannot be affected by ablation. If air is replaced with water, important processes such as melt-induced calving cannot be considered. For these particular cases, ablation can be defined normal to the surface. The surface mass-balance vector becomes
with b surf ⊥ < 0 the melting rate normal to the glacier surface. The general Hamilton-Jacobi Equation (4) then becomes non-linear. It reads

Equations (17) and (19) are presented as possible improvements of the method. They will not be evaluated or discussed.
Boundary conditions of the velocity-pressure problem
A vanishing pressure is adopted as the boundary condition for air
The pressure p can be specified anywhere in the air since the air density is set equal to zero and the dynamics is neglected. Therefore, the position of the boundary is arbitrary for the pressure condition.
Along the glacier base, two types of boundary condition can be specified. In the case of a frozen bed (no slip), the condition reads
where v is the ice velocity at the glacier bed. In the case of a temperate bed, the slip condition at the glacier bed is defined, first, by the ice motion normal to the bed
where v is the velocity of the ice to the bed, b edis the basal mass balance perpendicular to the bed (a positive value means melting of basal ice) and n bed the normal to the bed surface, pointing out of the ice. Second, it is defined by the tangential component of the viscous forces at the glacier bed
with f bed the tangent to the bed surface, pointing in the downstream direction, f bed the friction function and K = n bed the viscous force per unit area to the bed, with a the Cauchy stress tensor. For perfect slip (f bed = 0), Equation (23) reduces to
where εis the strain-rate tensor (Reference NyeNye, 1969, Reference Nye1970; Reference KambKamb, 1970; Reference PironneauPironneau, 1989; Reference Gresho and SaniGresho and Sani, 2000).
Boundary conditions of the level-set problem
In the glacier, the level-set boundary condition is expressed as
and in the air as
Since Equation (15) represents a purely advecting problem, boundary conditions are only imposed where the flux (ice and surface mass balance) enters the computational domain (Reference PironneauPironneau, 1989), i.e. where (n cd • v eff) < 0, with v eff = v + b surf the effective velocity and n cd the normal away from the computational domain.
Numerical Implementation
The model is implemented using the method of finite elements. The computations are performed in two dimensions.
Algorithm
A decoupling algorithm is used (e.g. Reference Picasso, Rappaz, Reist, Funk and BlatterPicasso and others, 2004); that is, the level-set equation and the flow equations are solved separately. At each time-step, Equation (15) is solved first using an implicit Euler scheme. The velocity is approximated with the results from the previous time-step. The conditions at the boundaries are given by Equations (25) and (26). This hyperbolic problem is solved with Lagrange elements of order two and stabilized with the streamline diffusion method (Reference PironneauPironneau, 1989). Then the flow model is computed by simultaneously solving the equations of mass and linear momentum balance

where the acceleration terms have been ignored. 2rj is the viscosity given by Equation (8), and p the density given by Equation (9). This set of non-linear equations (27) is solved by iteration on the viscosity. The maximum relative difference of the viscosity between two consecutive iterations is used as the criterion to stop the iteration procedure. To stabilize the pressure, the velocity variables are computed with second-order Lagrange elements, and the pressure with Lagrange elements of order one (Reference PironneauPironneau, 1989). The boundary conditions are given by Equations (20-24). Two different meshes are generated to solve the level-set and the flow models. Both meshes are composed of irregular triangular elements. Since V<p vanishes except in the vicinity of the interface, Equation (15) only gives rise to variations of <p near the interface. To reduce the computational time, a dense mesh is only used near the interface in the level-set computations. An iterative mesh refinement (Reference TrompertTrompert, 1995) is performed (on an initial sparse mesh) for every mesh cell located in the vicinity of the interface. After a fixed number of time-steps, a new refinement is performed, which takes into account the displacement of the ice-air interface. The refinement is performed on the basis of the results of the previous time-step. Therefore, only one solution of the level set is calculated for each time increment.
Validation
The numerical algorithm is validated by performing four tests: the evolution of an interface subject to a prescribed velocity field and a surface mass balance, the velocity profile of a parallel-sided slab surrounded by air, the deformation of an ice block without prescribed surface mass balance, and the analysis of the geometry of a glacier subject to a surface mass-balance function. Analytical or published numerical solutions exist for these four cases, with which the results of the model are compared. The first test analyzes the level set, while the second evaluates the flow problem. The last two tests consider the coupling of the level-set and the flow problems.
Figure 1a compares the evolution of a glacier surface computed with the level-set Equation (15) and calculated from the analytical solution in the case of a prescribed flow field given by vx(x, t) = x2 + z 2 and vz(x, t) = 0. For the analytical solution, the glacier surface is given by
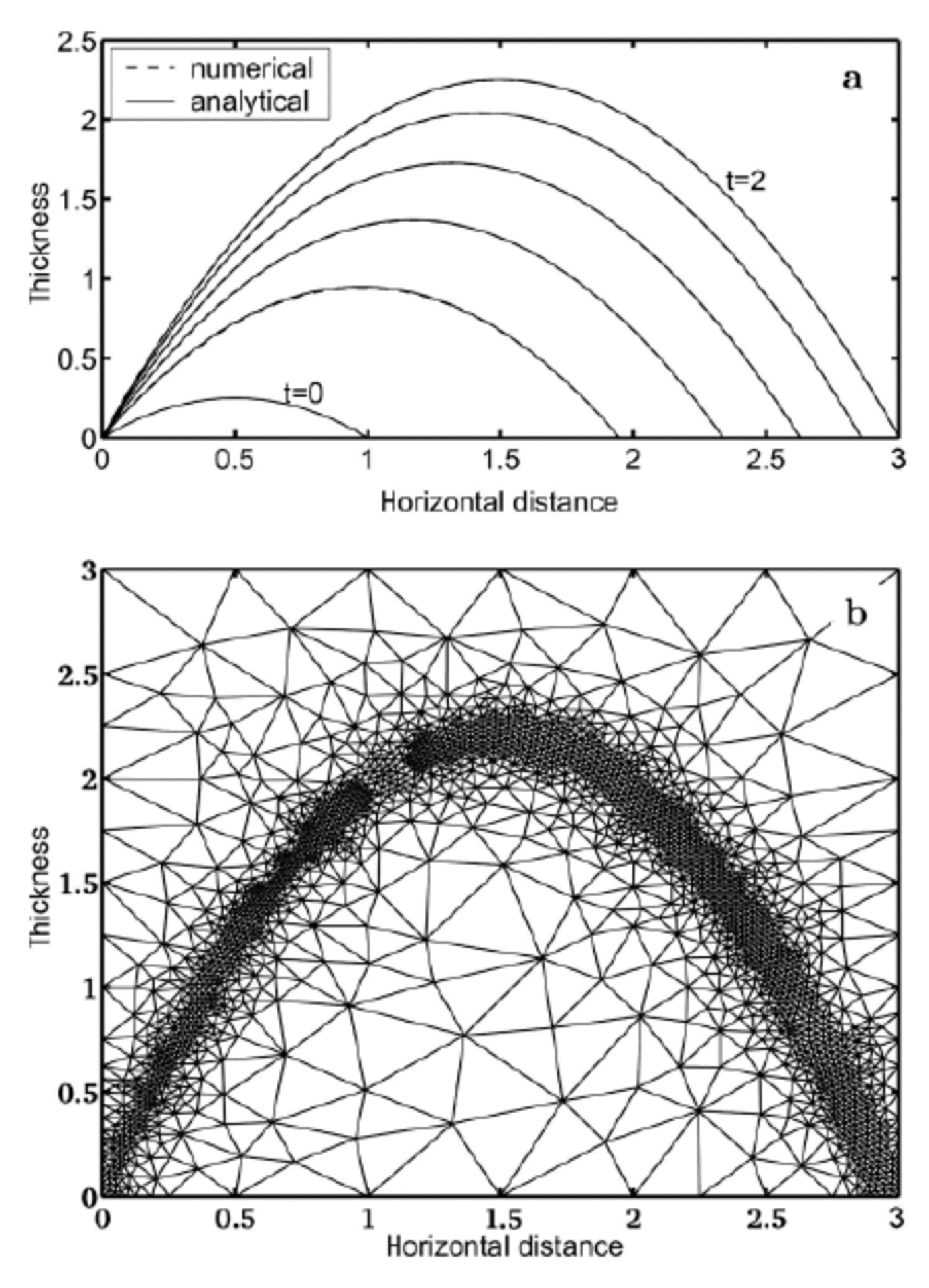
Fig. 1. (a) Evolution of an interface subject to an imposed surface mass balance and velocity field (see text) as obtained from the analytical (solid lines) and numerical (dashed lines; mostly coincident with solid lines) solutions. The initial position is given by t = 0, and the final position by t = 2. The problem is calculated and represented in a non-dimensional form. (b) Mesh used for computing the level-set equation at t = 2. This dense mesh is composed of 4703 elements.
s (x, t = x—x2+xt, and its length by l (t)= 1+ t (Reference Picasso, Rappaz, Reist, Funk and BlatterPicasso and others, 2004). For the numerical solution, the surface mass-balance function is chosen so that Equation (1) is fulfilled, i.e. b surf = x + (x 2 + z 2)(1 — 2x + t). Numerical results show a good agreement with the analytical solution. The ratio between the error (L 2)error of the interface position at the final time (t = 2) and the error at the beginning of the simulation (t = 0) is proportional to h 1.8, with h the size of the grid at the interface. The time-step is set proportional to h 1/2. The other parameters are kept constant. Figure 1b shows the mesh used to solve the final time-step of the interface evolution problem as presented by Figure 1a.
The second test considers the steady-state flow of an infinite inclined parallel-sided slab of ice surrounded by an air layer. The location of the ice-air interface is imposed (sp is here a fixed parameter). In the computational domain, the transition of viscosity and density at the ice-air interface is given by Equations (3), (8) and (9). Periodic boundary conditions are imposed in the longitudinal direction. The ice is considered to be frozen to the bed. The top of the air layer is a free surface. Figure 2 displays the non-dimensional velocity profile through the ice and air as computed by the numerical model. It is compared with the analytical solution of the problem (by setting 8 = 0 in Equation (3))

with vx th and vy th the theoretical horizontal and vertical velocities. By setting the parameter 8 proportional to h and keeping the other parameters constant, the computed velocities vx and vz converge to vx th and vy th
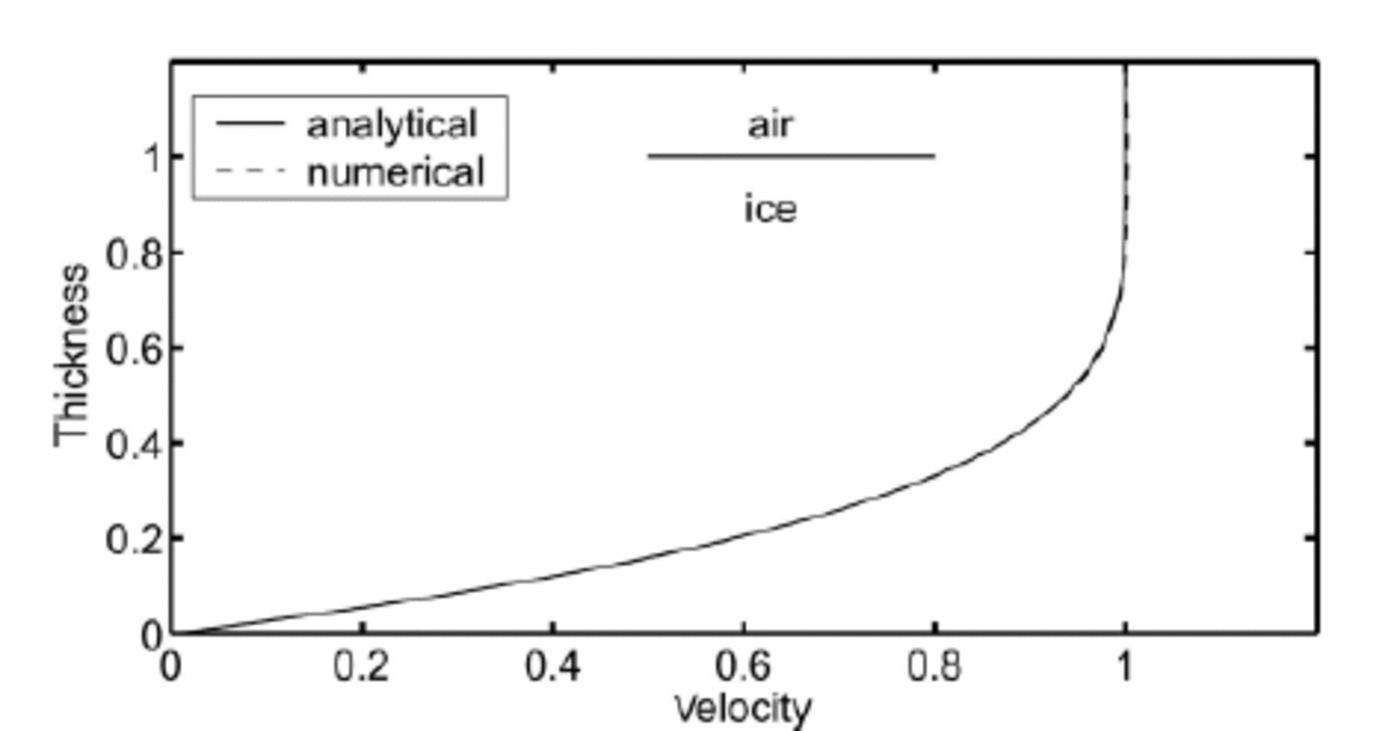
Fig. 2. Steady-state velocity profile through an infinite inclined parallel-sided slab as obtained from the analytical (solid line) and numerical (dashed line; mostly coincident with solid line) solutions. The problem is calculated and represented in a non-dimensional form. The ice is surrounded by air. The analytical and numerical solutions are calculated for the ice and air layers.
Figure 3a shows the deformation of an ice block creeping under its own weight. No mass balance is applied. To solve the ice-flow problem, the ice is considered to be frozen to the bed (bottom boundary of the computational domain). On the vertical wall on the left (left boundary), the ice may slip.bed = 0 and f bed = 0 are defined as slip parameters. The evolution of the geometry is calculated using the level-set method. Since the basal condition induces overriding processes during the deformation, the level-set solution is compared to a numerical solution obtained from a method describing overriding phenomena (Leysinger Reference Vieli, Funk and BlatterVieli and Gudmundsson, 2004). In both approaches, the ice flow is computed with the full Stokes equations (27). Both methods lead to similar solutions. The maximum separation (at the end of the computation) between the two curves represents 0.5% of the elevation of the undeformed ice block. In the computational domain, the volume of ice is evaluated at each time-step (by assuming an arbitrary constant glacier width). It should remain constant since the ice is incompressible. The relative error obtained by comparing the initial volume and the volume evolving with time is plotted in Figure 3b. The maximum error occurring during the computation amounts to approximately 0.2%. The error is associated principally with the finite-element discretization and the time integration of <p

Fig. 3. (a) Deformation of an ice block under its own weight on a horizontal surface. The computational domain is limited by the box. The level-set method (solid lines) and the boundary method (dotted lines) by Leysinger Reference Vieli, Funk and BlatterVieli and Gudmundsson (2004) are compared. Note the scale difference between the horizontal and vertical axes. The problem is calculated and represented in a non-dimensional form. (b) Error in per cent of the volume of ice as a function of the time-step for a level-set mesh composed of approximately 2700 elements. The last time-step corresponds to the last configuration (t2) presented in Figure 3a.
Figure 4a shows the temporal evolution of a glacier subject to a prescribed surface mass-balance function. The glacier bed has a slope of 35°. The initial condition represents a domain without ice. The surface mass-balance function
b surf ∥ varies along the x axis (parallel to the glacier bed) as
with a = —0.01 a-1. This corresponds to an accumulation at the upper part of the glacier (x u = —100m) of 1 ma–1. The ice is considered to be frozen to the bed (lower boundary). The ice may slip on the vertical wall on the left (left boundary). b bed = 0 and f bed = 0 are defined as slip parameters. The length of the glacier at steady state amounts to 199.1m. With the prescribed surface mass-balance function (29), the theoretical length of the glacier at steady state is obtained by

with xl the position of the lower part of the glacier. For solving Equation (30), the length of the glacier x l — xu = 200 m. At steady state, the relative error of the computed length with respect to the theoretical length amounts to 0.45%. The steady-state geometry of the glacier can also be calculated by solving the steady-state form of the level-set Equation (15) (by setting α = 0 in the general Hamilton-Jacobi Equation (4)) coupled with the flow equations system (27). The level-set and the flow equation are solved independently. An iterative process ensures the convergence of the system. A mesh refinement is performed for solving the level-set problem. The refinement is based here on the level-set solution of the present iteration. The mesh before refinement needs to be fine to ensure the convergence of the iterative process. To start the iteration, a rough guess of the steady-state solution of the glacier geometry is imposed (Fig. 4b). Several iterations between the level-set and the flow problem are necessary so that the solution tends to the steady-state geometry (Fig. 4b). By means of this procedure, the calculated length of the glacier <image>
reaches 200.3m. The relative error amounts to 0.15%. The error of the glacier length is in both cases associated with the finite-element discretization. Figure 4c compares the steady-state glacier geometry calculated using the level-set methods (direct steady state and time-dependent) and the kinematic boundary method (Equation (1)) for which a glacier length of 200 m has been imposed. The shape of the glacier is similar for all three approaches. Note the small instabilities near the glacier front for the kinematic boundary method. These are due to the difficulties encountered while computing the ice flow at the singular point of the front. The relative error between the kinematic boundary and the level-set curves is elsewhere <1%. Figure 4d compares the temporal evolution of the ice volume (by setting the glacier width at 1m) obtained with the numerical simulation and derived from the volume time-scale formula

with t equ the time required to reach steady state, V equ the volume of the glacier at steady state and q acc the prescribed total accumulation flux. Equation (31) was derived by linearizing the dynamics of the surface mass balance at t = 0. As long as the glacier length amounts to 100 m, the effective ice flux due to surface mass balance remains constant. During this period, the computed results should be identical to the theoretical result. By comparing the slope of the computed curve during the first 50years of simulation with the analytical slope, a relative error of 0.31% is determined.

Fig. 4. Calculation of the steady-state geometry of a glacier subject to accumulation and ablation. The glacier bed has a slope of 35 o . The computational domain is limited by the box. (a) Temporal evolution of the glacier calculated with the time-dependent level-set Equation (15). The initial configuration of the simulation is a domain without ice. The steady-state geometry is reached after approximately 180 years. At that stage, the level-set mesh is composed of approximately 3000 elements. (b) Geometries obtained during the iteration process for the calculation of the steady-state level-set equation (see text). The rectangle geometry represents the initial guess of the solution. After ten iterations, the final solution is reached. Approximately 10000 elements are used to solve the level-set problem. (c) Comparison of the steady-state geometry obtained with the steady-state method (Fig. 4b), with the time-dependent method (Fig. 4a) and with a kinematic boundary method (Equation (1)). (d) Temporal evolution of the volume of ice as calculated by the level-set method (Fig. 4a) and derived from the volume time-scale formula (Equation (31)).
Discussion
The convergence of the level-set algorithm is demonstrated for the general case of an advecting medium with a prescribed surface mass balance (Fig. 1). The convergence of the flow algorithm is presented in the case of an infinite parallel-sided slab (Fig. 2). The accuracy of the flow solution, in particular in the vicinity of the ice-air interface, indicates that the velocity v introduced in Equation (15) represents the physical velocity of the ice. Furthermore, as presented in Figures 3a and 4c, the air viscosity introduced for computing the level-set method has no noticeable influence on the ice dynamics. Thus, the level-set method adequately describes the evolution of the glacier surface. Further tests dealing with the conservation of the ice mass are presented for glaciers with and without prescribed surface mass balance (Figs 3c and 4d for evolving glaciers; Fig. 4a and b for glaciers in a steady state). These tests confirm the mass conservation of the coupled algorithm. The third test (Fig. 3) illustrates the possibility for modeling vertical fronts and overriding phenomena without adaptation of the method. The fourth test (Fig. 4) presents the capability of solving steady-state problems without time integration.
The computational time required to solve the level-set problem (including mesh refinement) as presented by the last two tests (Figs 3 and 4) is one order of magnitude smaller than the time needed for solving the full Stokes equations. The coupling of the level-set method with the shallow-ice approximation of the flow equations makes the level set less attractive with regard to the low time cost of the computation of the shallow ice flow. Fast resolution methods (e.g. the refinement method presented here, local computation of the level-set problem only near the interface (Reference Peng, Merriman, Osher, Zhao and KangPeng and others, 1999)) require, however, a number of discretization elements proportional to (1/h)d s -1, where h is the grid size near the interface and ds is the spatial dimension. They make the level-set methods competitive with kinematic boundary methods (Reference Osher and FedkiwOsher and Fedkiw, 2001).
Conclusions
The level-set method is a versatile approach for modeling the evolution of glaciers. A surface mass-balance function can be implemented easily. No difficulties are encountered in the modeling of discontinuous surfaces or vertical fronts. The description of topological changes of an evolving interface is handled naturally. The steady-state geometry of a glacier can be obtained by directly solving the steady-state form of the level-set equation coupled with the flow equations. The precision of the computed interface is, however, limited by the discretization of the level-set problem.
Other glaciological phenomena could be dealt with by this method, such as bed separation (Reference Schweizer and IkenSchweizer and Iken, 1992), R-channels (Reference Ro¨thlisbergerRo¨thlisberger, 1972), polythermal glaciers (Reference Blatter and HutterBlatter and Hutter, 1991) or calving processes (Reference Vieli, Funk and BlatterVieli and others, 2001).
Acknowledgements
We are indebted to A. Prohl for pointing out the pertinence of the level-set methods. We thank M. Raymond, T. Schuler and K. Hutter for critically reading the manuscript, the referees for helpful comments, which greatly improved the paper, and T. Jo´hannesson for his editing work and for many suggestions. This work was accomplished within the GLACIORISK project (Survey and Prevention of Extreme Glaciological Hazards in European Mountainous Regions) (grant No. EVG1-2000-00018 and BBW 00.0209-1).






