1. Introduction
Continental-scale ice sheets are an important element of the climate system. On a time-scale of decades, changes to the accumulation and melting on ice sheets force changes to global sea level, while at longer periods the waxing and waning of the great continental ice sheets is intimately connected to the evolution of the entire climate system (e.g. Reference Crowley and NorthCrowley and North, 1991). However, understanding the interaction between an ice sheet and the atmosphere is not straightforward. For example, the modeling of accumulation requires accounting for a wide range of physical processes, and spatial and temporal scales. Moreover, its distribution can be strongly influenced by the interaction between the atmospheric circulation and the surface topography. Secondly, the amount of ablation at an ice sheet’s margin is acutely sensitive to summer temperatures. Differences in temperature of 1°C lead to changes in the ablation rate of 1–2 m a−1 (e.g. Reference PollardPollard, 1980; Reference ReehReeh, 1991; Reference Calov and HutterCalov and Hutter, 1996). This strong sensitivity means that even for the modern climate state, current atmospheric general circulation models (AGCMs) are generally unable to simulate a climate consistent with the observed Greenland ice sheet (Reference PollardPollard and others, 2000).
The ice-sheet–atmosphere interaction is significant for a variety of paleoclimate questions. The origin and exact physical mechanisms of the quasi-periodic ice ages of the last 2 × 106 years remain unknown, and it is thought likely that instabilities of the ice sheet play a role in rapid climate-change events during glacial climates (e.g. Reference Crowley and NorthCrowley and North, 1991). Because it is impossible to integrate AGCMs for the thousands of years required to model ice dynamics, model studies typically employ a variety of simplified climate parameterizations. Temperature time series may be taken from an ice-core reconstruction (e.g. Reference GreveGreve, 1997; Reference Ritz, Fabre and LetréguillyRitz and others, 1997) or from the output of a simple energy-balance climate model (e.g. Reference PollardPollard, 1978, Reference Tarasov and PeltierTarasov and Peltier, 1997). Further, it is often assumed that the pattern of precipitation does not change from that of the current climate, and that the local accumulation amount is adjusted using the assumed or modeled surface temperature (e.g. Reference Tarasov and PeltierTarasov and Peltier, 1997; Reference Cuffey and MarshallCuffey and Marshall, 2000). It is likely, however, that an ice age leads to very different accumulation patterns. For example, the great ice sheets of the ice ages (the Laurentide over North America and the Fennoscandian over Eurasia) had a significant impact on the atmospheric circulation, including the location and intensity of storm tracks (e.g. Reference Hall, Valdes and DongHall and others, 1996; Reference Kageyama, Valdes, Ramstein, Hewitt and WyputtaKageyama and others, 1999).
Given the modeling difficulties noted above, it is important to understand how well the climate forcing needs to be known in order to model an ice sheet. If the ice sheet’s response is insensitive to the details of the accumulation and temperature distributions, then the crude approaches described above can provide robust answers. If, on the other hand, the ice sheet is acutely sensitive then such approaches will not provide useful information, and we might question whether the ice-age climate will ever be known well enough to provide a successful simulation of the ice-age ice sheets.
The focus of this study is on ascertaining what aspects of the accumulation pattern are important for modeling the response of an ice sheet. To examine this, we use the current Greenland ice sheet, whose topography is well known (Fig. 1) and for which there are several different accumulation datasets available. We examine the impact that each of these datasets has on the shape of the modeled ice sheet. We also use a simple parameterization to diagnose precipitation rates from observed winds and temperatures. This serves a two-fold purpose. First, the parameterization can be used to separate out which physical processes contributing to the precipitation are most important, and secondly we can assess whether simple parameterizations which take account of the atmospheric circulation might be used in ice-age studies.
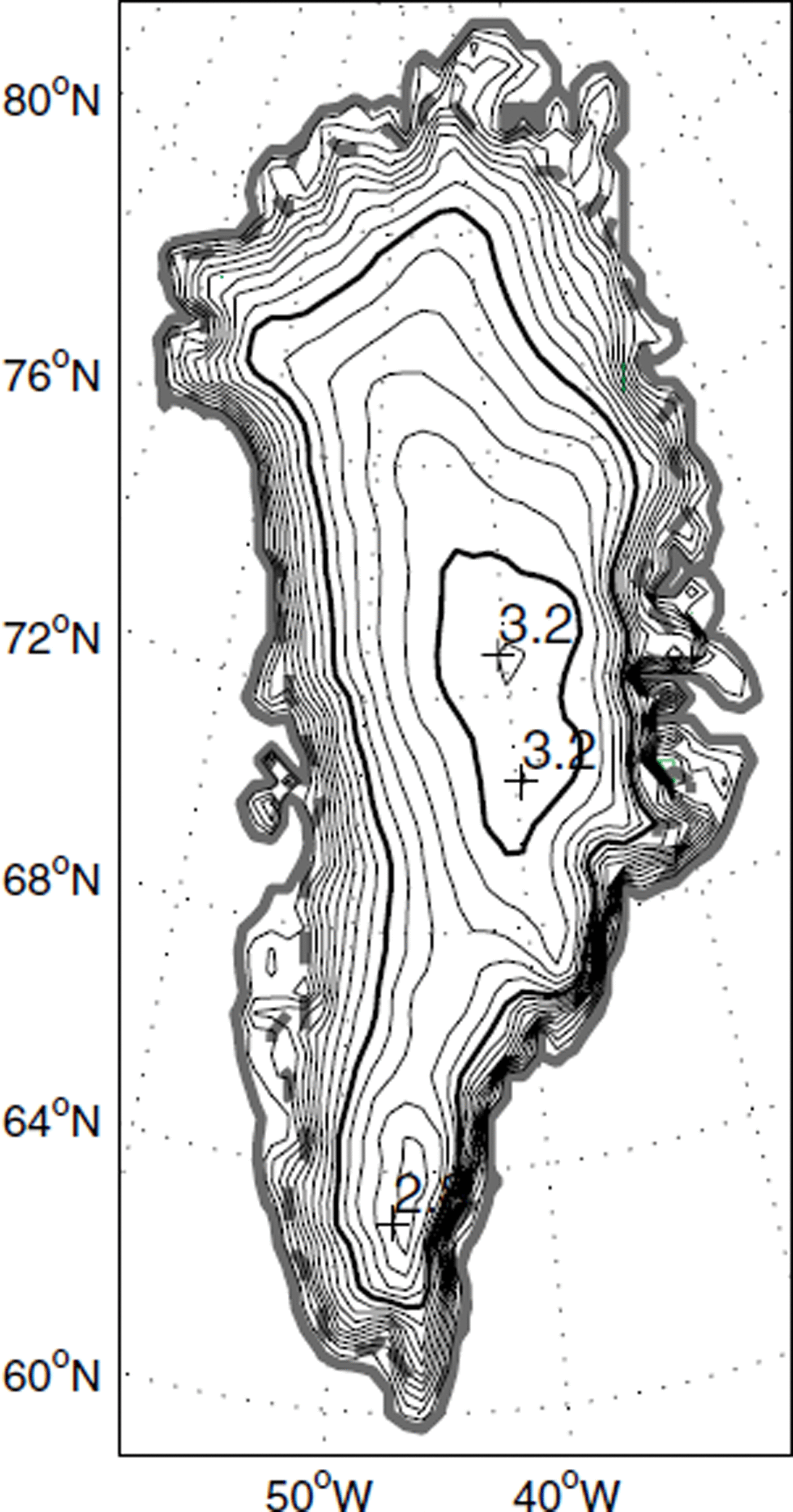
Fig 1. Observed Greenland topography. Data taken from Reference Letréguilly, Huybrechts and ReehLetréguilly and others (1991), except in a 160 km × 160 km window around the summit, where data from Reference Hodge, Wright, Bradley, Jacobel, Skou and VaughnHodge (1990) are used (Reference Greve, Weis and HutterGreve and others, 1998). Contour interval is 200 m; 2 and 3 km contours are emphasized. Solid gray line delimits Greenland coast; dashed green line delimits ice-sheet margin.
In section 3 we find that provided the accumulation decreases with temperature according to the overlying air column’s ability to hold moisture, then a reasonable simulation of the shape of the modern Greenland ice sheet results. However, in order to model the mass flux within the ice sheet, the effects of the atmospheric circulation interacting with the surface topography must be taken into account. The modeled ice-sheet shape is insensitive to small-scale variations in the accumulation distribution, especially if the variations occur around the ice-sheet margins. This is shown to be consistent with simple analytical models of ice flow. And while the accumulation pattern is likely important during the initial evolution of an ice sheet, the results suggest that, for modeling an ice sheet at a glacial maximum, simple precipitation schemes are probably sufficient.
2. Precipitation and Accumulation over Greenland
2.1. Datasets
Reference Ohmura and ReehOhmura and Reeh (1991) compiled a Greenland accumulation dataset (hereafter OR), combining direct snow-gauge observations with estimates from glaciological measurements (Fig. 2a). They found the average accumulation rate over the ice sheet to be 0.31 m a−1, with a maximum of around 1.5 m a−1 on the southeastern flank. Broadly speaking, the accumulation rate decreases with elevation and with latitude: the colder the temperature of the air column, the less moisture it is able to hold. Secondly, the local maxima and minima in the accumulation rate are attributable to the atmospheric circulation over Greenland (Reference Ohmura and ReehOhmura and Reeh, 1991). The low-level winds are generally anticyclonic, with some variation in strength and position over the course of the year. Where the prevailing winds are forced upslope on the ice sheet, there is enhanced precipitation because the rising air column cools and becomes saturated. Conversely, where prevailing winds are down-slope, precipitation is decreased: the so-called “rain shadow” effect observed in the lee of mountain ranges (e.g. Reference SmithSmith, 1979). There are also seasonal and regional variations in storminess over the ice sheet. During winter, for example, many storms impinge on the southeastern flank of the ice sheet, contributing to the high precipitation rates there (e.g. Reference Chen, Bromwich and BaiChen and others, 1997).

Fig 2. Different accumulation and precipitation datasets for Greenland. (a) Annual accumulation ratefrom Reference Ohmura and ReehOhmura and Reeh (1991); (b) ERA mean annual precipitation for 1985–93; and (c) Reference Chen, Bromwich and BaiChen and others (1997) annual precipitation rate diagnosed from MCEP re-analysis winds and temperatures (CBB). For clear comparison and to show interior accumulation detail, the color scale in each figure is truncated at 1 m a−1.
Ohmura and Reeh associate an accuracy of ±20% with the individual measurements used to produce Figure 2a. Because of this uncertainty, as well as the poor spatial and temporal coverage of the observations, there have also been attempts at some indirect, model-based estimates of the precipitation. Figure 2b shows the mean precipitation for the years 1985–93 from the European Centre for Medium-Range Weather Forecasts re-analysis project (hereafter ERA; Reference Gibson, Hernandez, Kållberg, Nomura, Serrano and UppalaGibson and others, 1996). The ERA re-analysis is a product of a numerical weather-prediction model which has meteorological observations assimilated into it as part of its operational cycle. The precipitation field is determined mainly by the numerical model rather than the direct observations. Since temperatures generally rise above zero only in summer, and then only over a relatively small fraction of the ice sheet, the precipitation rate in Figure 2b may be compared to the accumulation rate in Figure 2a. While the broad features of the distribution are the same, the ERA precipitation rate over the southeast is significantly higher than the OR precipitation rate, and the interior accumulation rate is much lower than observed — a recognized deficiency in the ERA data (Reference Bromwich, Cullather, Chen and CsathóBromwich and others, 1998).
Reference Chen, Bromwich and BaiChen and others (1997) made an independent estimate for precipitation over Greenland by diagnosing the vertical velocity in σ-coordinates using the U.S. National Centers for Environmental Prediction (NCEP) re-analysis dataset for horizontal winds, temperatures and relative humidity. Figure 2c is their estimate for the years 1985–95 (referred to hereafter as CBB). It is similar to the ERA data in that interior values are significantly underestimated. It also fails to show a local maximum in west central Greenland that appears in both the OR observations and the ERA re-analysis. Figure 2c does, however, show another observed local maximum in precipitation in northwest Greenland (close to Thule), not seen in the ERA.
2.2. Simple parameterization of precipitation
Here we outline a parameterization for precipitation that was used in Reference Roe and LindzenRoe and Lindzen (2001) for ice-age studies using a simple climate model. It was designed to represent the processes causing precipitation that were outlined in section 2.1. In section 3 it will be used to generate accumulation patterns to compare with the datasets already presented, and will be used to identify features of the distribution that are important for the response of an ice sheet.
The parameterization determines precipitation rates from time-mean (e.g. seasonal or monthly) wind and temperature fields, such as might be generated from a simple climate model. We assume that these fields are averaged over a time period that is much longer than the day-to-day synoptic variability. This variability is accounted for by including a probability distribution of vertical velocities, centered around the time-mean vertical velocity (method of calculation is described below). For the fraction of time for which the vertical velocity, w, is between w′ and w′ + dw′, the precipitation, dP, is taken to be
f(w′) is the probability of w being between w′ and w′ + dw′, and is defined below. a and b are constants. e sat is the saturation vapor pressure at the surface. It is given by the Clausius–Clapeyron equation (e.g. Reference HoltonHolton, 1992), and is a good proxy for the moisture content of the overlying air column. It is an exponential function of the surface temperature, T s : e Sat(T s)= e 0 exp[c 1 T s/(c 2 + T s)], where e 0 = 6.112 mbar, c i = 17.67 and c 2 = 243.5, and T s has units of °C. We take f (w′) as a Gaussian distribution centered on the time-mean vertical velocity, w 0:

N is a normalization factor to ensure that
![]() . The measure of variability of the vertical velocity, α, was taken to be 1.15 cm s−1, which was the average value over the region at 850 mbar, determined from daily NCEP data. A possible refinement of the parameterization would be to allow for α to vary with position (e.g. with proximity to the storm track). However, the results of section 3 show that this would probably have little impact on the resulting shape of the modeled ice sheet.
. The measure of variability of the vertical velocity, α, was taken to be 1.15 cm s−1, which was the average value over the region at 850 mbar, determined from daily NCEP data. A possible refinement of the parameterization would be to allow for α to vary with position (e.g. with proximity to the storm track). However, the results of section 3 show that this would probably have little impact on the resulting shape of the modeled ice sheet.
The precipitation rate for a given surface temperature is found by integrating Equation (1). The integral can be reduced to an expression involving error functions for which accurate asymptotic expansions are available (see Reference Roe and LindzenRoe and Lindzen, 2001).
Equation (1) can be related to the equation for conservation of water mass (Reference RoeRoe, 1999). This analysis shows that the parameter a roughly represents a background precipitation rate that would occur in the absence of time-mean vertical motion. A value for b can also be derived from this analysis, from which we take b = 5.9 × 10−9 s−3 kg−1. This value is similar to that used in a related parameterization (Reference Sanberg and OerlemansSanberg and Oerlemans, 1983; see also Reference RoeRoe, 1999), which was determined by tuning to observations over Scandinavia. That both approaches lead to similar numbers gives confidence that the parameterization yields physically plausible values.
The vertical velocity was determined by two separate methods. The first was to use the NCEP re-analysis dataset of pressure vertical velocity, ω, available on constant pressure surfaces on a 2.5° by 2.5° horizontal grid. On daily time-scales and longer, a good approximation is w
0 = − (H/p)ω, where p is the pressure and H is the atmospheric scale height (∼8.5 km). The second method was to calculate the vertical velocity using the relationship
![]() , where z
s is the surface topography and
, where z
s is the surface topography and
![]() is the horizontal wind (also taken from the NCEP re-analysis). This treatment assumes that all of the vertical motion is forced by flow over the topography. Over an ice sheet, however, there is a significant component which is due to air sinking over a cold surface. This second formulation therefore assumes that this sinking motion can be represented by its areal average and subsumed into the parameter a of Equation (1). The atmospheric data were interpolated onto the 40 km horizontal grid of the ice-sheet model (see section 3).
is the horizontal wind (also taken from the NCEP re-analysis). This treatment assumes that all of the vertical motion is forced by flow over the topography. Over an ice sheet, however, there is a significant component which is due to air sinking over a cold surface. This second formulation therefore assumes that this sinking motion can be represented by its areal average and subsumed into the parameter a of Equation (1). The atmospheric data were interpolated onto the 40 km horizontal grid of the ice-sheet model (see section 3).
In the model integrations presented below we use atmospheric data from the 850 mbar pressure surface, which has a mean height of about 1400 m. As seen from Figure 1, this level coincides with the steepest slopes on the ice sheet, and is therefore the most appropriate for the orographically induced accumulation. Where this pressure level lies below the physical surface of the ice sheet, the NCEP re-analysis gives values of
![]() and ω for directly above the surface. Data from the 1000, 925 and 700 mbar surfaces were also used to generate accumulation fields, and the differences were small. As long as the atmospheric fields change only slowly with height this will be true. The exception to this was that when data from the 700 mbar surface (average height 2800 m, generally well above the ice-sheet surface) were used, the accumulation rate on the southwestern flank of Greenland was excessive (compared to OR) due to the larger westerly winds at higher altitudes.
and ω for directly above the surface. Data from the 1000, 925 and 700 mbar surfaces were also used to generate accumulation fields, and the differences were small. As long as the atmospheric fields change only slowly with height this will be true. The exception to this was that when data from the 700 mbar surface (average height 2800 m, generally well above the ice-sheet surface) were used, the accumulation rate on the southwestern flank of Greenland was excessive (compared to OR) due to the larger westerly winds at higher altitudes.
The accumulation rate for Greenland was determined from Equation (1) using the observed topography and monthly-mean NCEP re-analysis data, averaged between 1985 and 1995 (for comparison with CBB), and using the NCEP 2 m temperature for Ts . Precipitation was deemed to fall as snow if the monthly-mean T s was < 0°C, although the results were not sensitive to this choice. Any rainfall was assumed to run off the ice sheet. Monthly accumulation rates were summed to give the annual accumulation rate. Note that there is an implicit smoothing associated with the 40 km grid spacing, and also from using the 2.5° by 2.5° NCEP re-analysis data.
The focus of this work is to compare an ice sheet’s response to different patterns of accumulation, and so the accumulation rate was calculated as described above, adjusting the value of a in Equation (1) until the mean accumulation rate over the ice sheet agreed with the OR observations (0.31 m a−1).
3. Equilibrium Integrations of an Ice-Sheet Model
The different accumulation datasets and the simplified accumulation parameterization are now used as climate forcing for a series of equilibrium model integrations to simulate the modern Greenland ice sheet. The ice-sheet model we use is the SICOPOLIS model of Reference GreveGreve (1997). Ice is treated as a non-Newtonian, isotropic, viscous, thermomechanical fluid obeying Glen’s flow law (e.g. Reference PatersonPaterson, 1994). The model includes the temperate layer (a mix of ice and water) that forms if the internal and geothermal heating raises the basal temperature above melting point. The horizontal resolution of the model was taken as 40 km, resulting in 42 × 71 gridpoints covering Greenland. The vertical resolution is 51 gridpoints in the cold-ice region and 11 in the temperate-ice region. In the integrations presented below, we use the set of parameters given in Reference GreveGreve (1997), where further details of the model may be found. If the ice sheet reaches the coastal margin it is assumed to calve into the ocean, and the height there is set to zero.
Ablation is calculated using the positive degree-day (PDD) approach as implemented by Reference Calov and HutterCalov and Hutter (1996). The PDDs at any given location are the integrated positive temperatures over the year, and are regarded as a melting potential with different ablation rates assumed for ice and snow. To calculate the PDDs, the SICOPOLIS code takes the temperatures from a parameterization of observations due to Reference ReehReeh (1991). There is an inconsistency between the temperature used to calculate the ablation and the temperatures used to calculate the accumulation rate (i.e. the NCEP re-analysis). However, since the purpose of this study is to examine the response of the ice sheet to changes in accumulation patterns only, everything else is held fixed in the model integrations.
3.1. Model integrations using accumulation datasets
For all of the runs presented, the model is initiated with the current Greenland topography and integrated for 100 kyr, which is sufficient time for the model to come to equilibrium with the forcing climate. A summary of all the results is presented in Table 1.
Table 1. Summary of ice-sheet model integrations

The model integration using the OR-observed accumulation produces a good simulation of the observed ice sheet (Fig. 3a). Differences are that the maximum height is slightly overestimated (by 40 m), and the modeled ice sheet is overextended slightly in the northwest of Greenland. Another minor discrepancy is that the axis of the southern dome has a slightly different orientation. Overall, though, the area, volume and maximum height of the ice sheet are well simulated.

Fig. 3. Result of integrating SICOPOLIS model using OR accumulation data, (a) Surface topography, contours every 200 m; (b) contours and vectors of vertically integrated mass flux. Contour interval 60 km m a−1
The vertically integrated mass flux (Fig. 3b) also reflects the overlying accumulation distribution, although not directly. In steady state, the divergence of the mass flux is equal to the local net mass balance (i.e. including surficial and basal melting). Furthermore, probably the most important determinant of the mass flux is the basal topography: high mass flux occurs over low basal elevations and within bedrock channels (see, e.g., Reference Letréguilly, Huybrechts and ReehLetréguilly and others (1991) and Fig. 5b (shown later), a model integration using uniform accumulation). However, if all other factors stay the same then a higher accumulation rate drives a larger mass-flux divergence, and leads to a larger mass flux. This relationship between ice flux and accumulation has important consequences for the internal ice dynamics. Regions of high mass flux produce greater internal frictional heating which can raise the basal temperature to the melting point. When this occurs, the ice is no longer frozen to the bedrock but becomes free to slide. Areas of the ice sheet with temperate ice at the bottom coincide closely with the contoured regions of high mass flux in Figure 3b.
The CBB dataset was available as monthly precipitation rates. To convert it to an annual accumulation rate it was assumed that precipitation fell as snow if the NCEP re-analysis mean monthly 2 m temperature was < 0°C, and the monthly rates were summed over the annual cycle. This processing only affects the accumulation rate at low elevations in southern Greenland, and has little impact on the modeled ice sheet. The resulting pattern was also multiplied by 0.97 so that the average accumulation rate was the same as the OR observations. The equilibrium ice sheet obtained by integrating the ice-sheet model with this accumulation pattern is shown in Figure 4a. The most obvious difference from Figure 3a (the OR accumulation) is that the lower accumulation rate in the northern interior causes an underestimate of the volume and maximum height. Moreover, the peak of the northern dome sits much closer to the coast at a location where there is only a secondary maximum in the observations. Differences in the accumulation pattern are also reflected in the mass flux. The weaker accumulation rate in North Greenland produces a much weaker mass flux there (Fig. 3b). In southern Greenland the mass flux agrees fairly well in the two integrations.

Fig. 4. As for Figure 3, but for SICOPOLIS integration using CBB accumulation data.
A model integration was performed using the ERA precipitation dataset, processed to give an accumulation rate in the way described above. It produced an ice sheet that looked very similar to that using the CBB dataset, and the results are summarized in Table 1.
Caution is required in comparing these model integrations to the observed ice sheet. The dynamical adjustment time-scale for an ice sheet the size of Greenland is several thousand years, and in general, therefore, it is not going to be in equilibrium with the climate forcing at any given time. However, paleoclimate records in the region indicate that the climate has been comparatively stable in the region over the last 10 kyr (e.g. Reference DansgaardDansgaard and others, 1993), so we might expect the Greenland ice sheet to be fairly close to equilibrium. Addressing this question, Reference Ritz, Fabre and LetréguillyRitz and others (1997) performed a time-dependent simulation of the Greenland ice sheet using a plausible reconstruction of the climate forcing over the last glacial cycle. They compared the resulting ice sheet for the current time to an ice sheet that was in steady state with the current climate forcing. For a range of parameters used in the ice model, the maximum height and volume in the steady-state integration were about 5% and 10% smaller, respectively, than in the transient run. Reference GreveGreve (1997) found similar results.
Because the CBB and ERA distributions have known deficiencies (Reference Bromwich, Cullather, Chen and CsathóBromwich and others, 1998), and because of the good agreement between the observed ice sheet and that modeled using the OR accumulation (especially their overall shape), the model integrations in this section support the OR observations as being closer to the actual accumulation distribution than either the CBB or ERA datasets. Therefore we shall compare the model integrations produced using the accumulation parameterization presented in section 2.2 to Figure 3a and b.
3.2. Model integrations using accumulation parameterization
We now examine what features of the accumulation pattern are necessary to model the Greenland ice sheet. The simplest possible pattern is a uniform accumulation field equal to the average of the OR observations (0.31 m a−1). The equilibrium ice sheet from an integration using this forcing is shown in Figure 5a. While the area is close to the observed value, both the volume and maximum height are significantly overestimated (Table 1): too much snow accumulating in the interior leads to an excessive build-up of the ice there. Comparing to the integration using OR observations, the differences in ice mass flux reflect the differences in accumulation rates (Fig. 5b). The mass flux is significantly over-predicted in northern and central Greenland, while it is under-predicted along the southern coast.

Fig. 5. As for Figure 3, but for integration using uniform accumulation field.
Next an accumulation pattern is generated only from the surface temperature observations. The procedure outlined in section 2.2 followed, but with the parameter b set to zero. Thus the winds do not influence the accumulation distribution, which includes only the effect that decreasing temperature with elevation and latitude reduces the ability of an air column to hold moisture. The parameter a in Equation (1) is adjusted so that the average accumulation rate over the ice sheet is the same as in the OR observations, and the resulting pattern is shown in Figure 6a. The accumulation rate in the Greenland interior is slightly overestimated, and while there is a band of maximum accumulation around the southern coast, it is not as large as in the OR observations. Figure 6a confirms, as was argued in section 2.1, that it is the atmospheric circulation that generates these features.

Fig. 6. (a) Accumulation derived using simplified parameterization with surface temperature dependence T s only; (b) surface height, contours every 200 m; and (c) contours and vectors of vertically integrated mass flux. Contour interval 60 km m a−1.
Using this accumulation forcing, the SICOPOLIS model gives the equilibrium ice sheet shown in Figure 6b. The area, maximum height and volume all agree quite closely with observations (Table 1). The main discrepancy with the integration performed using the OR observations is the ice mass flux, and again there is a clear connection to the accumulation-rate differences. The mass flux in the northern half of the ice sheet is overestimated, and around the southern margin it is underestimated (Fig. 6c).
The next step is to include the effect of the atmospheric circulation on the accumulation distribution. The accumulation field determined from Equation (1), using
![]() and data from 850 mbar, is shown in Figure 7a. The gridscale variability is attributable to having interpolated the coarse-resolution atmospheric data onto the finer grid on which the topography is calculated. Comparing with the OR observations (Fig. 2a), the localized maximum on the southeast coast is seen (although substantially over-predicted), as is the minimum in the southwest. The local maximum near Thule also appears, although again over-predicted. In the interior, the accumulation rate is about equal to the OR observations. Overall, while the large-scale features are fairly well captured, there is a lot of small-scale variation, and exaggeration of localized maxima and minima.
and data from 850 mbar, is shown in Figure 7a. The gridscale variability is attributable to having interpolated the coarse-resolution atmospheric data onto the finer grid on which the topography is calculated. Comparing with the OR observations (Fig. 2a), the localized maximum on the southeast coast is seen (although substantially over-predicted), as is the minimum in the southwest. The local maximum near Thule also appears, although again over-predicted. In the interior, the accumulation rate is about equal to the OR observations. Overall, while the large-scale features are fairly well captured, there is a lot of small-scale variation, and exaggeration of localized maxima and minima.

Fig. 7 As for Figure 6, but including dependence on atmospheric circulation (i.e. using
![]() ).
).
The integration of the SICOPOLIS model with this accumulation is shown in Figure 7b. It is notable that even though the accumulation field has substantial gridscale noise, the resulting ice sheet is much smoother. The diffusive nature of ice flow is highly effective in smoothing out small-scale variations in the accumulation rate. The overall shape of the ice sheet resembles the observed, except in southwest Greenland where the underestimation of accumulation rate has caused the ice sheet to thin and recede.
The regions of high mass flux within the ice sheet (Fig. 7c) agree well with those obtained using the OR accumulation, although there is some overestimate of the ice flux in the southeast where there is excessive accumulation. That the mass flux agrees more closely than either the uniform or temperature-dependent accumulation patterns demonstrates that capturing the interaction between the prevailing winds and the surface topography is necessary to successfully model the underlying ice dynamics.
An accumulation pattern was also generated using the NCEP re-analysis ω to calculate ω 0 in Equation (1). This approach produced an accumulation pattern that picked up the circulation features seen in the OR observations, although smeared out. When it was used as climate forcing, the SICOPOLIS model reproduced the shape of the ice sheet (Table 1). The modeled mass flux, however, did not do as well as that seen in Figure 7c in capturing the variations seen in the integration using the OR accumulation.
In summary, the overall shape of the Greenland ice sheet is quite robust to different patterns of accumulation. Only in the model integration forced by uniform accumulation did the error exceed 10% (Table 1), and then only in volume. So the results suggest that provided the accumulation rate decreases with surface temperature, following the Clausius–Clapeyron equation, the model integration will produce an ice sheet resembling the modern one. However, the mass flux within the ice sheet is a more sensitive measure of the local accumulation distribution, and reflects quite strongly the differences in accumulation pattern caused by the prevailing atmospheric circulation.
As already mentioned, the ice mass flux is closely connected with an ice sheet’s basal boundary condition, changes to which have been invoked as an explanation of the periodic discharge of large parts of the Laurentide ice sheet during Heinrich events (Reference MacAyealMacAyeal, 1993). An implication of the results here therefore is that the successful modeling of such events in climate models likely requires knowledge of the atmospheric circulation controlling the accumulation distribution over the ice sheet.
3.3. Sensitivity to mean accumulation rate
The accumulation patterns used in section 3.2 all had the same mean value. To test the sensitivity of the ice sheet to changes in this value, a series of integrations were performed using the OR accumulation multiplied by a factor varying from 0.5 to 2.0. For this range, the area and maximum height of the equilibrium ice sheet varied by ±10%, and the volume by ±20%. This relative insensitivity of the ice sheet to mean accumulation rate is consistent with simple models of ice flow (e.g. Reference PatersonPaterson, 1994). A coastal margin is fixed by calving processes, and a land-based margin is constrained because ablation is a strong function of temperature: an increase in accumulation rate causes only a small advance in the ice-sheet margin before it encounters warm enough temperatures for the ablation to balance the increased accumulation.
4. Analytical Solutions for an Idealized Ice Sheet
The results of the previous section showed that the modeled ice sheet was insensitive to small-scale accumulation variations and especially to details of the accumulation around the margin. Some light can be shed on these results by considering simple models of ice flow within ice sheets.
If bedrock depression and the temperature dependence of the flow are neglected then to a good approximation the profile of a steady-state two-dimensional ice sheet (height and length) is the solution to the following equation (e.g. Reference PatersonPaterson, 1994):

where H is the height of the ice sheet, and x is the horizontal coordinate. A is a constant (taken to be 10−23 s−1 Pa−3), ρ i is the density of ice, and a c(x) is the accumulation rate. The exponent, n, is normally taken to be 3 (e.g. Reference PatersonPaterson, 1994). Equation (3) can be thought of as a non-linear diffusion equation, in which the coefficient, D, is a function of the height and slope of the ice sheet. For given boundary conditions, Equation (3) may be solved analytically for uniform accumulation rate (e.g. Reference PatersonPaterson, 1994). Assuming that the ice sheet is calving at a coastal margin, and taking a fixed center-to-margin length of 800 km and a uniform accumulation rate of 0.3 m a−1, Equation (3) gives an ice sheet 3.2 km in height.
In the Appendix it is shown how the analytic solution can be modified to include the effects of a δ-function accumulation anomaly. That is, we take a c(x) = a 0 + a 1Δxδ (x − x 0). Figure 8 shows the effect on the ice-sheet profile of adding an accumulation anomaly at different places over the ice sheet. In all cases, a 0 = 0.3 m a−1 and a 1Δx = 120 km m a−1 The closer to the center of the ice sheet the anomaly is placed, the larger the impact on the ice sheet. When the anomaly is placed 100 km from the center, the volume change is 7.2%, and the height increases by 250 m. When it is placed 100 km from the margin, the volume change is only 1.8%, and the height is raised only 30 m.

Fig. 8. Response of an idealized ice-sheet model to an accumulation perturbation located at different points along the ice sheet (at the value of x0 denoted in the legend).The solution is derived in the Appendix. In all cases a 0 = 0.3 m a−2 and a 1Δx = 120 km m a−1.
At each point along the ice sheet the flux of ice must, in steady state, balance the accumulation upslope (i.e. upflow) of that point. An anomaly located close to the middle of an ice sheet represents a greater fraction of the integrated accumulation up to that point than does an anomaly located towards the margin, so it is perhaps not surprising that the impact is greatest there. Another interpretation of the results in Figure 8 is that viewed from the upslope side, an accumulation anomaly acts to reduce dH/dx. If dH/dx decreases, H must increase until Equation (3) can be satisfied. Close to the center of the ice sheet, where dH/dx is smaller, the perturbation provides a much greater relative forcing on the slope than a perturbation near the margin, so the ice-sheet response is proportionately larger.
In all cases in Figure 8, even when the anomaly is located close to the margin, the height adjustment takes place over the whole ice sheet and demonstrates that flow of ice is extremely effective in diffusing local variations in accumulation rate (see section 3). Reference Boudreaux and RaymondBoudreaux and Raymond (1997) also found this to be true in similar calculations applied to glaciers.
These results have some positive implications for ice-sheet modeling. Firstly, small-scale structure in the accumulation field has little impact on the resulting ice sheet, at least in equilibrium. Secondly, different ice-age climate models are likely to produce the largest differences in accumulation patterns at the margins of ice sheets. It is there that differences in modeled atmospheric circulation will combine with the steepness of the slopes to produce the largest effect on the accumulation rate. However, it is precisely at the margin that these differences have the least impact on the shape of the modeled ice sheet.
5. Summary and Discussion
Simulations of the modern Greenland ice sheet have been performed using a variety of accumulation distributions. Of those considered, it appears that the Ohmura–Reeh dataset is closest to reality. However the overall shape of the ice sheet can be reasonably reproduced provided that the accumulation decreases with elevation according to the Clausius–Clapeyron equation. Consistent with results from simple models, this is due to the highly diffusive nature of ice flow, which is extremely effective in smoothing out the small-scale variations in accumulation rate.
The simplified accumulation parameterization that was presented was able to reproduce fairly well the major features of the accumulation distribution influenced by the topography. This suggests that when coupled to simplified climate models, such schemes might be used to investigate the interaction of the atmospheric circulation and ice sheets on ice-age time-scales. However, the model results also showed that the ice mass flux reflected the overlying atmospheric circulation. This suggests an additional mechanism whereby climate changes affect ice dynamics, and furthermore that ice-age theories which involve changes to the ice sheet’s mass flux ought to account for the interaction between the prevailing winds and the surface topography. It is stressed that the parameterization presented still depends on knowing the winds and temperatures over the ice sheet.
The relative insensitivity of the ice-sheet shape to the accumulation pattern highlights the importance of summertime melting. The simulation of an ice sheet at a particular climate state (e.g. the Last Glacial Maximum) is much more sensitive to small changes in the summertime temperature than to small changes in the accumulation (e.g. Reference PollardPollard and others, 2000). However, accumulation is likely more important for the early growth of an ice sheet. For instance, Reference Roe and LindzenRoe and Lindzen (2001) considered an idealized configuration for the development of an ice sheet away from a coastline. High accumulation rates on the windward side of the developing ice sheet produced a rapid migration of the ice sheet in the direction of the prevailing winds, which continued until the ice margin reached the coastline. Successful modeling of an advancing ice sheet therefore requires knowledge of the atmospheric circulation.
The interaction between an ice sheet and the rest of the climate system involves numerous and complex physical processes. The purpose of this paper has been to begin to better understand which of those processes are the most crucial in addressing some of the many significant questions which arise out of that interaction.
Acknowledgements
Insightful and constructive reviews from A. Ohmura and R. Calov led to a much improved manuscript and are gratefully appreciated. Thanks to R. Greve for help with SICOPOLIS, to D. Bromwich and E. Sinclair for help with their data, and also to C. Raymond, E. Waddington, and E. DeWeaver. This is a Joint Institute for the Study of the Atmosphere and Ocean contribution No. 912.
Appendix
Analytical Solution for Simple Flow Model Incorporating an Accumulation Anomaly
If the peak of the ice sheet is at x = 0, and the ice margin is at x = L, then Equation (3) can be written as:

If the accumulation is uniform, and the ice sheet has a fixed length (it is assumed to be constrained by a coastline), then standard solutions exist for Equation (A1) (e.g. Reference PatersonPaterson, 1994). Here the solution is extended to examine the response of the ice sheet to an accumulation anomaly.
We take a uniform accumulation rate plus a delta function anomaly located at a point, x 0, somewhere on the ice sheet: a c(x) = a 0 + a 1Δxδ(x − x 0). Integrating Equation (A1) gives separate equations up- and downstream of the anomaly:


where
![]() is a point an infinitesimal distance upflow of the anomaly, H
d is the maximum height of the ice sheet (at x = 0),
is a point an infinitesimal distance upflow of the anomaly, H
d is the maximum height of the ice sheet (at x = 0),
![]() is the height at
is the height at
![]() , and H′ and x′ are dummy variables of integration. The applicable boundary conditions are as follows:
, and H′ and x′ are dummy variables of integration. The applicable boundary conditions are as follows:
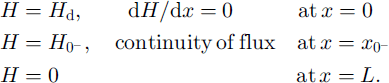
Using boundary condition (A4)1, Equation (A2) gives that between x = 0 and
![]()
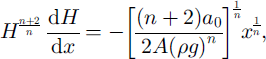
which can be integrated again between x = 0 and
![]() :
:

From Equation (A3), we get that for
![]()
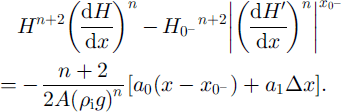
But Equation (A2) and boundary condition (A4)2 demand that
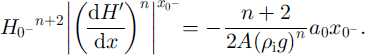
Substituting this into Equation (A7), rearranging and integrating between
![]() and x yields
and x yields
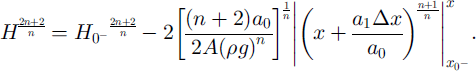
Combining Equations (A5) and (A9) eliminates
![]() , and using boundary condition (A4)3 gives H
d:
, and using boundary condition (A4)3 gives H
d:

Finally, we get to an exact expression for H:

Where

If a
1 = 0, or if
![]() , then the standard Vialov–Nye solution is recovered (e.g. Reference PatersonPaterson, 1994). The same analysis can be gone through for a Gaussian-shaped accumulation anomaly with a finite width, instead of a δ function. The results are very similar, which is a further indication of the very diffusive nature of ice flow.
, then the standard Vialov–Nye solution is recovered (e.g. Reference PatersonPaterson, 1994). The same analysis can be gone through for a Gaussian-shaped accumulation anomaly with a finite width, instead of a δ function. The results are very similar, which is a further indication of the very diffusive nature of ice flow.










