A corrected solution method is presented for a mathematical model of wave motions in a coupled ice-shelf/sub-ice-shelf water-cavity system. The method is used to calculate the periods of the system's normal modes, and the longest periods are shown to be significantly larger than those calculated using an existing method containing errors. Highly accurate approximations of the normal-mode periods are obtained for a model involving a single non-spectral physical parameter – the shelf/cavity length.

Recently, it has been recognised that long, tsunami or infragravity (IG) waves generated by storms at distant continental coasts occasionally impact Antarctic ice shelves and ice tongues, to an extent that enhance iceberg calving. Although the ice thickness and the depth of the underlying sea water cavity are hundreds of metres, they are substantially less than incoming tsunami or IG wavelengths of several kilometres or more and a shelf length of tens to hundreds of kilometres. Sergienko (Reference Sergienko2013) sought the so-called normal modes of an ice-shelf/sub-ice-shelf water-cavity system, i.e. the resonant standing waves that can be excited at certain periods/frequencies, using a one-dimensional thin-plate/shallow-water model, for a uniform shelf (constant thickness and material properties) and shallow-water cavity of constant depth. However, her solution method contained a fundamental error in the complex roots of the dispersion relation that significantly simplified calculation of the normal modes.

This letter corrects the expressions for the complex roots of the dispersion relation, and outlines a solution method for the more complicated resulting system of equations. The corrections are shown to significantly increase the longest periods of the normal modes, but to have small impacts on shorter periods. Further, a non-dimensionalisation is used to reduce the material properties of the shelf and cavity and their vertical dimensions, to a single parameter, which reveals that the only non-spectral physical parameter necessary to calculate the normal modes is the length of the shelf/cavity.

Following Sergienko (Reference Sergienko2013), the shelf is assumed to be of length L and uniform thickness h ≪ L, and the cavity beneath it of uniform depth H. The coordinate x is used to denote horizontal locations along the shelf/cavity, with its origin set to coincide with the seaward end of the shelf and x = −L denoting the landward end.

Under the usual assumptions of linear water-wave theory, the water velocity field in the cavity is defined as the gradient of a scalar potential function Φ. As the wavelengths are assumed to be far greater than the water depth and the wave steepness to be small, the potential satisfies the linear shallow-water equation

(1) $$\displaystyle{{\partial ^2 \Phi} \over {\partial x^2}} =- \displaystyle{{ 1} \over H}\displaystyle{{\partial \eta} \over {\partial t}},$$

where η(x, t) is the elevation of the water surface, t denotes time and Φ = Φ(x, t). Sergienko (Reference Sergienko2013) applied no-flux conditions at the ends of the cavity

(2) $$\displaystyle{{\partial \Phi} \over {\partial x}} = 0\quad {\rm at}\quad x = - L,\;0,$$

where the condition at the landward end, x = −L, implies no penetration through the solid boundary and the condition at the seaward end, x = 0, implies motions in the shelf–cavity system that are trapped/resonant.

Assuming the shelf and water remain in contact at all points x ∈ ( − L, 0) and at all times during the motion, η denotes the vertical displacements of the lower surface of the shelf. As the shelf is assumed to be thin with respect to its length and the wavelengths, Sergienko (Reference Sergienko2013) modelled the shelf as a thin elastic plate, meaning its strain field can be determined from the displacement function satisfying

(3) $$D\displaystyle{{\partial ^4 \eta} \over {\partial x^4}} + \rho _{\rm i} h\displaystyle{{\partial ^2 \eta} \over {\partial t^2}} + \rho _{\rm w} g\eta = - \rho _{\rm w} \displaystyle{{\partial \Phi} \over {\partial t}}.$$

Here g ≈ 9.81 m s⁻² is the constant of gravitational acceleration, ρ _w ≈ 1024 kg m⁻³ and ρ _i are water and ice densities, respectively, and D = Eh ³/{12(1 − ν ²)} is the flexural rigidity of the shelf, where E is its effective Young's modulus and ν ≈ 0.33 its Poisson's ratio. The right-hand side denotes pressure forcing due to water motion in the cavity. The shelf is clamped at its landward end via the conditions

(4a) $$\eta = 0\quad {\rm and}\quad \displaystyle{{\partial \eta} \over {\partial x}} = 0\quad {\rm at}\quad x = - L,$$

and free at its seaward end, with conditions

(4b) $$\displaystyle{{\partial ^2 \eta} \over {\partial x^2}} = 0\quad {\rm and}\quad \displaystyle{{\partial ^3 \eta} \over {\partial x^3}} = 0\quad {\rm at}\quad x = 0.$$

A non-dimensionalisation is applied (similar to that of Fox, Reference Fox, Dempsey and Shen2001), by defining non-dimensional spatial and temporal coordinates as, respectively,

(5) $$\hat x = \displaystyle{x \over {L_{\rm c}}} \quad {\rm and}\quad \hat t = \displaystyle{t \over {t_{\rm c}}}, $$

where

(6) $$L_{\rm c} = \root 4 \of {\displaystyle{D \over {\rho _{\rm w} g}}} \quad {\rm and}\quad t_{\rm c} = \sqrt {\displaystyle{{\rho _{\rm w} L_{\rm c}^6} \over {DH}}}, $$

are the characteristic length and time, respectively. This normalises the wave speed to unity, since

(7) $$\hat c = \displaystyle{{ct_{\rm c}} \over {L_{\rm c}}} = \sqrt {\displaystyle{{gHt_{\rm c}^2} \over {L_{\rm c}^2}}} = \sqrt {\displaystyle{{\rho _{\rm w} gHL_{\rm c}^4} \over {DH}}} = 1.$$

Non-dimensional versions of (1) and (3) are combined into a single governing equation for motion of the coupled shelf–cavity system, by eliminating the displacement function, to give

(8) $$\displaystyle{{\partial ^6 \Phi} \over {\partial x^6}} - \displaystyle{{\partial ^2 \Phi} \over {\partial t^2}} + \displaystyle{{\partial ^2 \Phi} \over {\partial x^2}} + M\displaystyle{{\partial ^4 \Phi} \over {\partial t^2 \partial x^2}} = 0\quad {\rm for}\quad x \in ( - L,0).$$

The hat notation has been dropped for clarity, on the understanding that x, t, L and Φ are non-dimensional during presentation of the solution methods. Equation (8) depends on the single parameter

(9) $$M = \displaystyle{{\rho _{\rm i} hH} \over {\rho _{\rm w} L_{\rm c}^2}}, $$

where M ≪ 1 typically.

Time-harmonic solutions of (8) are sought with (non-dimensional) angular frequency ω, by writing

(10) $$\Phi = {\rm Re}{\kern 1pt} \{ X(x)\exp ( - {\rm i}\omega t)\}, $$

where ${\rm Re}{\kern 1pt} \{ \bullet \} $ denotes the real part of the included function. Equation (8) becomes

(11) $$\displaystyle{{{\rm d}^6 X} \over {{\rm d}x^6}} + (1 - M\omega ^2 )\displaystyle{{{\rm d}^2 X} \over {{\rm d}x^2}} + \omega ^2 X = 0,$$

with associated boundary conditions

(12a) $$\displaystyle{{\partial X} \over {\partial x}} = 0,\quad \displaystyle{{\partial ^2 X} \over {\partial x^2}} = 0\quad {\rm and}\quad \displaystyle{{\partial ^3 X} \over {\partial x^3}} = 0\quad {\rm at}\;\;x = - L,$$

and

(12b) $$\displaystyle{{\partial X} \over {\partial x}} = 0,\quad \displaystyle{{\partial ^4 X} \over {\partial x^4}} = 0\quad {\rm and}\quad \displaystyle{{\partial ^5 X} \over {\partial x^5}} = 0\quad {\rm at}\quad x = 0,$$

derived from non-dimensional versions of (2) and (4). The problem is to determine the positive eigenfrequencies ω = ω ₁, ω ₂, …>0 and corresponding eigenfunctions X(x) = X ₁ (x), X ₂ (x), … for which non-trivial solutions of (11) and (12) exist. The problem is self-adjoint, meaning the eigenfrequencies are real-valued; this can be shown formally by applying the Rayleigh quotient to the variational form of the problem. The eigenfrequencies are indexed in ascending order ω ₁ <ω ₂ <…, noting the model is valid for low frequencies only.

Sergienko (Reference Sergienko2013) sought solutions of (11) of the form exp (± iαx), where the wavenumber α(ω) is such that β = α ² satisfies the dispersion relation

(13) $$\beta ^3 + p(\omega )\beta + q(\omega ) = 0,$$

where

(14) $$p = 1 - M\omega ^2 \quad {\rm and}\quad q = - \omega ^2. $$

Focusing on the low-frequency/long-wave regime, the coefficient p > 0, meaning the depressed cubic (13) has a unique positive real root

(15) $$\beta (u_0 ) = u_0 - \displaystyle{\,p \over {3u_0}} \equiv \beta _0, $$

where u ₀ is the real root u of

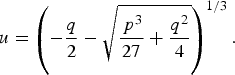(16) $$u = \left( { - \displaystyle{q \over 2} - \sqrt {\displaystyle{{\,p^3} \over {27}} + \displaystyle{{q^2} \over 4}}} \right)^{1/3}. $$

The corresponding real wavenumber is $\alpha _0 = \sqrt {\beta _0} \gt 0$ , with the positive branch of the square-root chosen, so that exp (+ iα ₀ x) is a rightward-propagating wave and exp ( − iα ₀ x) is a leftward-propagating wave. The remaining two roots of (13) are denoted β = β _±1. They are complex-valued and such that $\beta _1 = \overline {\beta _{ - 1}} $ , where the overbar denotes complex conjugation. (Cubic (13) has three real roots for frequencies high enough that p < 0, although this is outside the regime of model validity.)

Sergienko (Reference Sergienko2013) assumed the complex roots β _±1 are equal to the products of the real root β ₀ and the complex cube roots of unity, i.e.

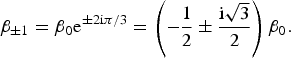(17) $$\beta _{ \pm 1} = \beta _0 {\rm e}^{ \pm 2{\rm i}\pi /3} = \left( { - \displaystyle{1 \over 2} \pm \displaystyle{{{\rm i}\sqrt 3} \over 2}} \right)\beta _0. $$

The corresponding complex-valued wavenumbers are

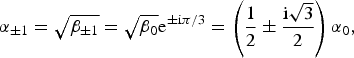(18) $$\alpha _{ \pm 1} = \sqrt {\beta _{ \pm 1}} = \sqrt {\beta _0} {\rm e}^{ \pm {\rm i}\pi /3} = \left( {\displaystyle{1 \over 2} \pm \displaystyle{{{\rm i}\sqrt 3} \over 2}} \right)\alpha _0, $$

where branches of the square-root are chosen such that ${\rm Re}{\kern 1pt} \{ \alpha _{ \pm 1} \} \gt 0$ . The imaginary components of wavenumbers α _±1 cause the associated waves to grow/decay along the coupled shelf/cavity system.

Sergienko (Reference Sergienko2013) therefore expressed the general solution of (11) in a form equivalent to

(19) $$\eqalign{X(x:\alpha _0 ) = & \sum\limits_ \pm \left\{ {C_{ - 1}^{( \pm )} {\rm e}^{ \pm {\rm i((1/2)} - ({\rm i}\sqrt 3 /2){\rm )}\alpha _0 x} + C_0^{( \pm )} {\rm e}^{ \pm {\rm i}\alpha _0 x}} \right. \cr & + \left. {C_1^{( \pm )} {\rm e}^{ \pm {\rm i((1/2)} + ({\rm i}\sqrt 3 /2){\rm )}\alpha _0 x}} \right\},} $$

where the $C_n^{( \pm )} $ (n = −1, 0, 1) are amplitudes. She proceeded to substitute (19) into boundary conditions (12a) and (12b) to produce a system of six homogeneous linear equations for the six amplitudes, in which the coefficients depend on the scaled wavenumber γ = α ₀ L only, rendering it analogous to seeking normal modes of a vibrating string. Non-trivial solutions were obtained by calculating numerically the countable infinity of values γ = γ _n (n = 1, 2, …) for which the determinant of the system equals zero. The normal modes of the problem are $\Phi _n = {\rm Re}{\kern 1pt} \{ X_n (x)\exp ( - {\rm i}\omega _n t)\} $ (n = 1, 2, …), where X _n and ω _n are the eigenfunction and frequency corresponding to γ _n , with X _n (x) = X(x:α ₀ = γ _n /L), and ω _n calculated numerically from (15) and (16) for β ₀ = (γ _n /L)², once the physical parameters are specified.

Assumption (17) is incorrect – in general, the roots of the depressed cubic (13) cannot be expressed in terms of a single parameter, as Sergienko (Reference Sergienko2013) did using β ₀. Instead, the complex roots are β _±1 ≡ β(u _±1), where u _±1 are the two complex solutions of (16)

(20) $$u = u_{ \pm 1} = u_0 \exp \left( {\displaystyle{{ \pm 2\pi{\rm i}} \over 3}} \right),$$

so that

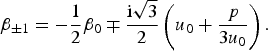(21) $$\beta _{ \pm 1} = - \displaystyle{1 \over 2}\beta _0 \mp \displaystyle{{{\rm i}\sqrt 3} \over 2}\left( {u_0 + \displaystyle{\,p \over {3u_0}}} \right).$$

Roots β _±1 differ from those used by Sergienko (Reference Sergienko2013), (17), in their imaginary parts – the components that induce the associated waves to grow/decay – but, fundamentally, depend on the physical parameters (M and L) and spectral parameter (ω) through u ₀ and p, in addition to β ₀.

Figure 1 shows the imaginary part of β ₊₁ used by Sergienko (Reference Sergienko2013) and used here, as a function of non-dimensional frequency ω, for M = 0.0162. In the low-frequency limit, ω → 0, Sergienko (Reference Sergienko2013)'s ${\rm Im}{\kern 1pt} (\beta _{ + 1} )$ vanishes, as it is proportional to β ₀ → 0 as ω → 0. In comparison, the imaginary part of β ₊₁ given by (21) tends to unity in the low-frequency limit. As the frequency increases, the ${\rm Im}{\kern 1pt} (\beta _{ + 1} )$ s get closer to one another, because the p/3u ₀ term begins to dominate over the u ₀ term.

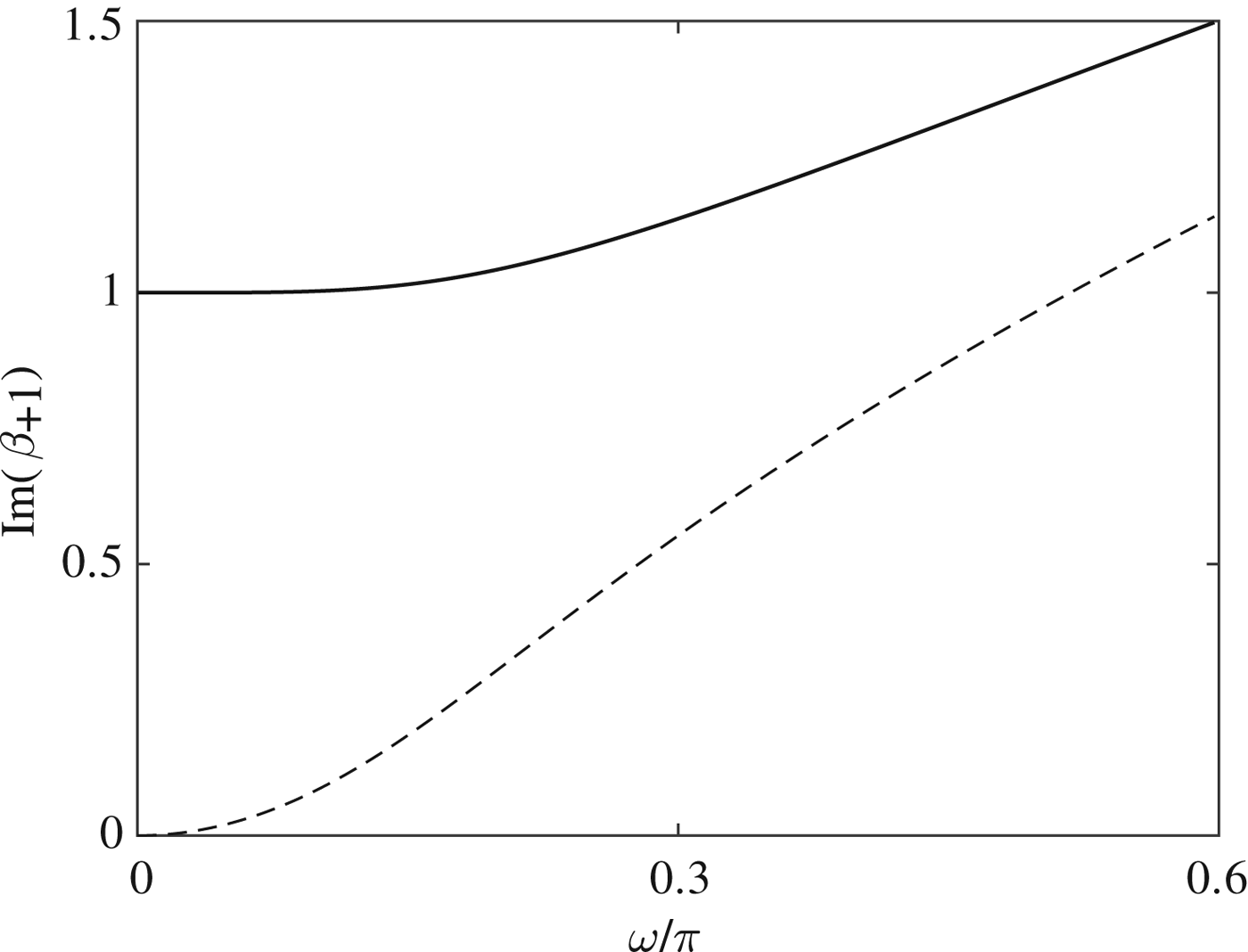
Fig. 1. Imaginary part of complex root β ₊₁, as used by Sergienko (Reference Sergienko2013) (dashed line) and used here (solid line), given by (17) and (21), respectively, as a function of non-dimensional angular frequency for M = 0.0162.

Using the corrected imaginary roots, the general solution becomes

(22) $$X(x) = \sum\limits_ \pm \left\{ {C_{ - 1}^{( \pm )} {\rm e}^{ \pm {\rm i}\alpha _{ - 1} x} + C_0^{( \pm )} {\rm e}^{ \pm {\rm i}\alpha _0 x} + C_1^{( \pm )} {\rm e}^{ \pm {\rm i}\alpha _1 x}} \right\}.$$

The wavenumbers

(23) $$\alpha _{ \pm 1} = \sqrt {\beta _{ \pm 1}} = A(\cos (\psi ) \pm {\rm i}\sin (\psi )),$$

where

(24) $$A = \root 4 \of {\beta _0^2 + p} \quad {\rm and}\quad \psi = \arctan \left( {\displaystyle{{\sqrt 3 (\,p + 3u_0^2 )} \over {\,p - 3u_0^2}}} \right),$$

with branches chosen such that ${\rm Re}{\kern 1pt} \{ \alpha _{ \pm 1} \} \gt 0$ and $ \pm {\rm Im}{\kern 1pt} \{ \alpha _{ \pm 1} \} \gt 0$ . Thus, the corrected wavenumbers differ from those of Sergienko (Reference Sergienko2013) in both real (wavelength) and imaginary (growth/decay rate) components.

Figure 2 shows the real and imaginary parts of α ₊₁ used by Sergienko (Reference Sergienko2013) and used here, as functions of non-dimensional frequency ω, for M = 0.0162. Similarly to ${\rm Im}{\kern 1pt} (\beta _{ + 1} )$ , in the low-frequency limit, Sergienko (Reference Sergienko2013)'s ${\rm Re}{\kern 1pt} (\alpha _{ + 1} )$ and ${\rm Im}{\kern 1pt} (\alpha _{ + 1} )$ vanish and the corrected values tend to a non-zero limit, and as frequency increases the corresponding values move closer together.

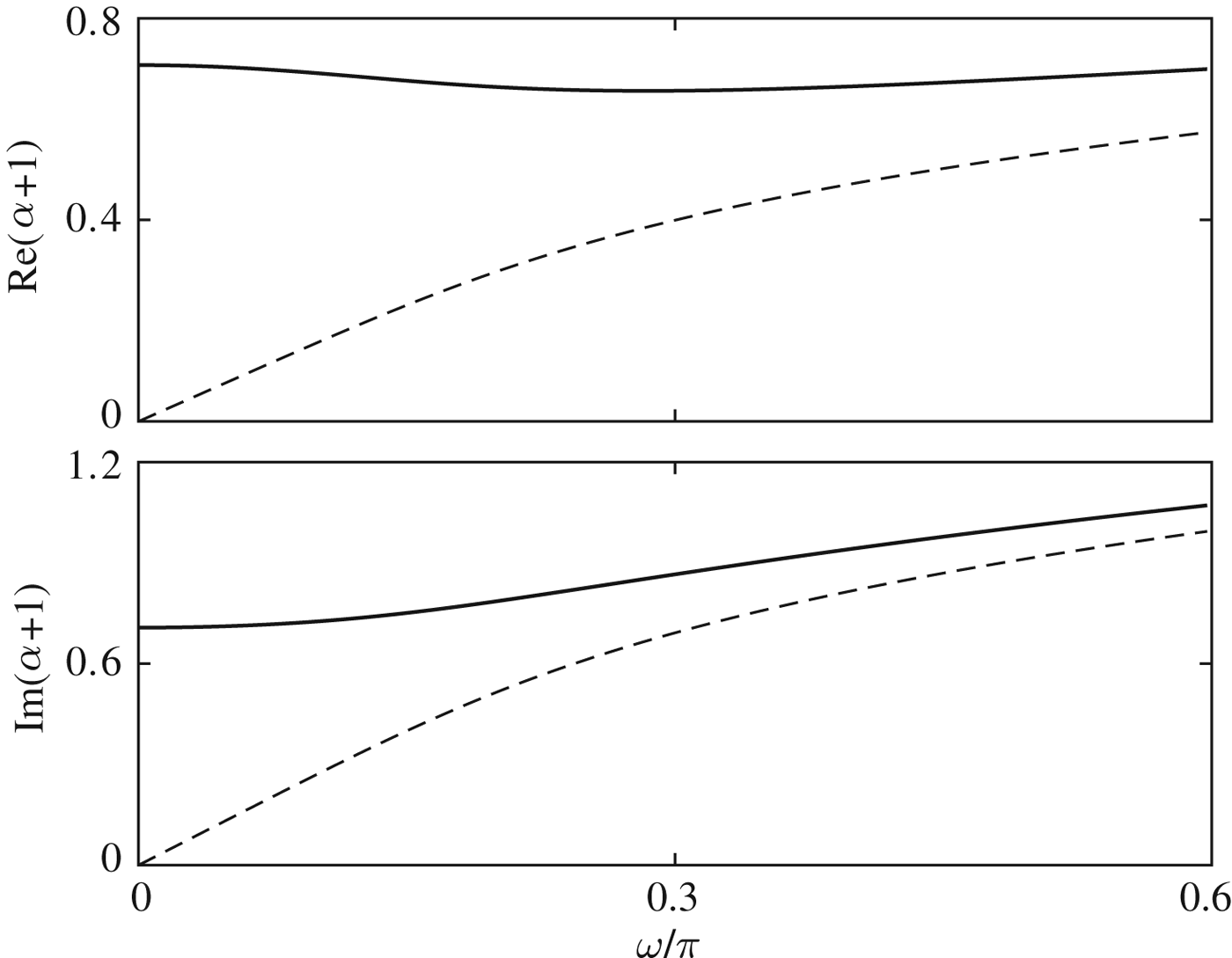
Fig. 2. Real and imaginary parts of complex wavenumber α ₊₁, as used by Sergienko (Reference Sergienko2013) (dashed line) and used here (solid line), given by (18) and (23), respectively, as a function of non-dimensional angular frequency for M = 0.0162.

Substituting general solution (22) into boundary conditions (12a) and (12b) produces a system of six homogeneous linear equations for the six amplitudes, as in Sergienko (Reference Sergienko2013). This is expressed in matrix form as

(25) $${\bf Ac} = {\bf 0},$$

where the 6 × 6 matrix

(26a) $$\{ {\bf A}\} _{i,j} = ( - {\rm i}\alpha _{\,j - 2} )^i \exp ({\rm i}\alpha _{\,j - 2} L),$$

(26b) $$\{ {\bf A}\} _{i,3 + j} = ({\rm i}\alpha _{\,j - 2} )^i \exp ( - {\rm i}\alpha _{\,j - 2} L),$$

for i, j = 1, 2, 3,

(26c) $$\{ {\bf A}\} _{4,j} = - \alpha _{\,j - 2}, \quad \{ {\bf A}\} _{4,3 + j} = \alpha _{\,j - 2} $$

for j = 1, 2, 3,

(26d) $$\{ {\bf A}\} _{4 + i,j} = ( - {\rm i}\alpha _{\,j - 2} )^{3 + i}, $$

and

(26e) $$\{ {\bf A}\} _{4 + i,3 + j} = ({\rm i}\alpha _{\,j - 2} )^{3 + i}, $$

for i = 1, 2 and j = 1, 2, 3, contains the coefficients of the system, the vector

(27) $${\bf c} = \left[ {C_{ - 1}^{( - )}, C_0^{( - )}, C_1^{( - )}, C_{ - 1}^{( + )}, C_0^{( + )}, C_1^{( + )}} \right]^T $$

contains the amplitudes, and 0 is a column vector of length 6 containing zeros.

The coefficients contained in ${\bf A}$ depend on three scaled wavenumbers α _n L (n = −1, 0, 1), which are related to one another by their dependencies on the three physical/spectral parameters M, L and ω, thus making it impractical to seek zeros of the determinant in terms of them. Alternatively, the coefficients are considered to depend on the physical parameters M and L, and squared spectral parameter ω ², with values ω ² = φ _n (n = 1, 2, …) calculated at which the determinant of the system vanishes for specified M and L. The eigenfrequencies are recovered simply as $\omega _n = \sqrt \varphi_{n} $ (n = 1, 2, …). This contrasts with Sergienko (Reference Sergienko2013)'s method of seeking values of the spectral parameter γ at which the determinant of her system vanishes, without reference to physical parameters.

The shelf thickness, density and Young's modulus, and cavity depth are set as h = 300 m, ρ _i = 917 kg m⁻³, E = 11 GPa and H = 100 m (as in Bromirski and Stephen, Reference Bromirski and Stephen2012), giving non-dimensional parameter M = 0.0162. Table 1 shows the dimensional periods (T _n ) associated with the some of the lowest eigenfrequencies, produced by Sergienko (Reference Sergienko2013)'s method and the corrected method, for shelf length L = 40 km. The non-dimensional eigenfrequencies for these periods are <π/2, meaning they are contained in the intervals used for Figures 1, 2.

Table 1. Periods (T _n ) of normal modes for L = 40 km

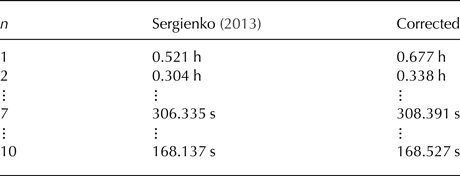
The longest periods are ~0.5 h, i.e. in the tsunami-wave regime. Periods predicted by the corrected method are longer than those predicted by Sergienko (Reference Sergienko2013)'s method, with the longest period ~30% larger for the corrected method, and ~11% larger for the second longest period. The impact of the errors in Sergienko (Reference Sergienko2013)'s method decrease as the periods decrease (frequencies increase) and the errors in complex wavenumbers diminish. For the order 100 s periods shown – the IG-wave regime – the corrected periods T ₇ and T ₁₀ are only ~0.7% and ~0.2% larger than their counterparts, respectively.

Figure 3 shows the quotient of the longest period (T ₁) calculated using the correct method ( $T_1^{{\rm corr}} $ ) on the value calculated using Sergienko (Reference Sergienko2013)'s method ( $T_1^{{\rm Serg}} $ ) as a function of shelf/cavity length in the interval 10–100 km. The quotient is greater than unity over the interval, meaning the corrected period is consistently longer than the period calculated using Sergienko (Reference Sergienko2013)'s method. Its value monotonically increases with respect to increasing length, with rapid increase from ~1.1 to ~1.3 over L = 10–50 km, followed by a slower rate of increase for L > 50 km.

Fig. 3. Quotient of the longest period (T ₁) calculated using the corrected method on the value calculated using Sergienko (Reference Sergienko2013)'s method, as a function of shelf/cavity length.

For the longest periods, i.e. the lowest frequencies, p(ω) ≈ 1, as the non-dimensional parameter M ≪ 1, meaning the cubic (13) depends on the spectral parameter ω only. Figure 4 shows the 20 longest periods for the parameters used in Table 1, and the periods calculated using M = 0 (p = 1). The periods match almost exactly, with the difference ~0.01% for the longest period and increasing only to ~3.4% for the 20th longest period, indicating dominance of shelf flexure over inertia.

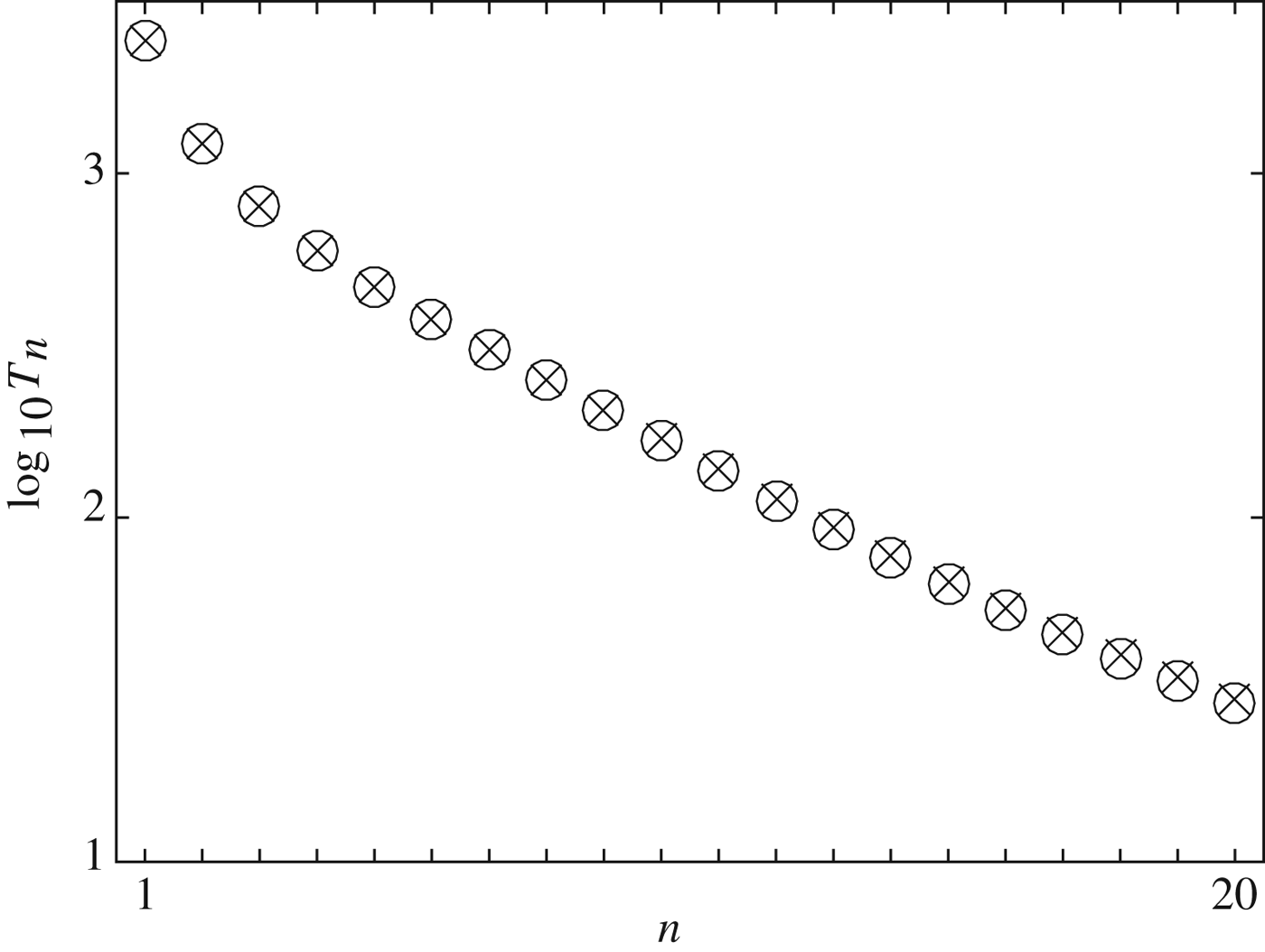
Fig. 4. Twenty longest periods of normal modes, calculated with M = 0.0162 (×) and M = 0 (○).