List of Symbols

Introduction
Sliding over hard bedrock with cavity formation has been a subject of great interest and has been treated extensively (Reference LliboutryLliboutry. 1968; Reference IkenIken, 1981; Reference KambKamb, 1987). Reference LliboutryLliboutry (1979) and Reference FowlerFowler (1986) have derived sliding laws allowing for bed separation. They have provided graphical solutions for sliding over periodic beds.
Reference Budd, Keage and BlundyBudd and others (1979) and Reference BindschadlerBindschadler (1983) originally proposed a sliding law of the form
to fit observations, Budd’s interpretation has been discussed by Reference LliboutryLliboutry (1987). Similar laws were found theoretically by Reference LliboutryLliboutry (1978) and Reference FowlerFowler (1987). Here, ub is the sliding velocity, T is the basal shear stress, N is the effective pressure (overburden pressure minus water pressure), the exponent m is often set equal to the exponent n in Glen’s flow law (in the absence of regelation) and d is an empirical positive number.
This sliding law incoporates an instability as N approaches zero, i.e. the water pressure approaches the ice-overburden pressure.
However, the sliding law in Equation (1) does not allow for an instability at a critical pressure, p0, that is lower than the overburden pressurep0. Reference IkenIken (1981) has shown the existence of such an instability at a pressure

where β is the maximum angle between the mean bed and stoss faces.The obvious contradiction between the existence of this critical pressure and the sliding law in Equation (1) was our motivation to derive a different sliding law that incorporates this instability.
Sliding Velocity Near the Critical Pressure
Assumptions
To carry out the calculations described below, we need to make the following simplifying assumptions:
(i) We consider a sinusoidal bed of small roughness and large wavelengths (so that regelation is negligible).
(ii) Plane strain is assumed.
(iii) The ice is separated from the bedrock by a thin water film, i.e. the interface supports no shear stresses.
(iv) All cavities contain water at the same pressure.
(v) The water pressure is close to the critical pressure.
We will make the point that assumption (v) means that the contact area between ice and bedrock is very small and is centered around the point of inflection on the stoss faces of the bed undulations. This is not immediately clear, since Gudmundsson (1994) has shown that for a sinusoidal bed (amplitude a and wavelength l) the pressure maxima are to be found at values of x which solves

(his equation 4.38). The pressure maxima are at the inflection points for small roughness only. However, Equation (3) was derived for a bed without bed separation. We deal with a situation if extensive bed separation. This affects the stress distribution considerably. In the case of almost complete bed separation, the contact point has to be exactly at the inflection point, because otherwise the instability would occur at a pressure that is even lower than the critical pressure. This can be seen by inspecting the balance of forces on the segment of basal ice shown in figure 1a. If the contact area was located at a point different from the inflection point, a new Equation (2) could be derived by a similar analysis. In this new equation, the angle β would be replaced by an angle β’ < β, β’ being the angle between the mean bed and the tangent at the supposed point of contact. This would lead to an even lower critical pressure. In the same way, one can show that the length of the contact zone must become very small as the water pressure approaches the critical value. Here, we bear in mind that the pressure on a contact area is, by definition, greater than the water pressure.
Stresses at the ice—bedrock contact area
The analysis is based on a force. balance acting on an element of basal ice shown in figure 1a. This element extends over one wavelength, l, in the x direction, and has a unit thickness in the y direction. The mean stresses along the upper boundary, AB, of the element are the macroscopic stresses p0 and T. The lower boundary does not support any shear stress (assumption (iii) above).The normal stress is pw on the roof of the cavity and there is a mean normal stress of tz’z’ at the contact area. The contact area is defined as that part of the bed where the pressure on the bed is larger than the water pressure in the cavity. It is indicated in figure 1b by a bold line of length Δl.

Fig. 1. Scheme of the glacier base: large, water-filled cavities between ice and sinusoidal bed, which is shown by a hatched line. (a) Element of basal ice (stippled area), to which the force balance refers. The upper boundary of the element, AB, is parallel to the mean bed and extends over one wavelength l. The lower boundary is the glacier sole between A and B; T and p0 are the mean stresses on the upper boundary. They are equal to the macroscopic stresses. (b) Coordinate systems. The x axis is chosen along the mean bed of slope α, while the x1 axis is along the steepest tangent to the bedrock, β is the angle between the two axes. The area of contact between ice and bed, △l, is marked by a bold line. The shapes of the cavities are not exactly known but they are irrelevant for the analysis.
A force balance in the z’ direction yields the stress component tz’z’, the mean normal stress on the contact area:
β is again the largest angle between the mean bed and the actual bed. s* = △l/l is a dimensionless number for the size of the contact area. The first term on the righthand side represents the contribution of the shear stress, the second the contribution of the overburden and the third the contribution of the water pressure to the force balance. The signs in the above equation reflect the fact that the stresses are compressive p0 and pw are taken to be positive).
The critical pressure (Equation (2)) is obtained by formulating a similar force balance in the x’ direction and calculating that water pressure, at which all forces in the x’ direction balance. This pressure is a limiting value. At higher water pressures, an acceleration along x’ would result.
The stress calculated in Equation (4) is a principal stress, since the water film does not support any shear stress. The second principal stress is taken to be equal to the water pressure pw. This is correct as long as the contact area is small, as can be seen by calculating the Airy stress function. The limiting case of an infinitely small region has been treated in textbooks on elasticity (e.g. Jaeger, 1971, section 36).
We can thus calculate the deviatoric stress:

p0 can now be replaced by using Equation (2):

Sliding velocity
Using the above-calculated deviatoric stress and Glen’s flow law ![]() with Teff given by
with Teff given by ![]() we obtain the strain rate εz’z’. This constitutive law is used somewhat arbitrarily since the magnitude and transience of the stress field put it outside the realms of “normal" glacial flow. We now make the additional assumption that the strain rates are effective over a normal distance corresponding to the width of the contact area Δl. This assumption is justified in a linear theory and approximately applies here. We can therefore use the stresses at the interface to estimate a deformational velocity perpendicular to the bed at the contact area.
we obtain the strain rate εz’z’. This constitutive law is used somewhat arbitrarily since the magnitude and transience of the stress field put it outside the realms of “normal" glacial flow. We now make the additional assumption that the strain rates are effective over a normal distance corresponding to the width of the contact area Δl. This assumption is justified in a linear theory and approximately applies here. We can therefore use the stresses at the interface to estimate a deformational velocity perpendicular to the bed at the contact area.

Note that Equation (7) was derived without using the assumption of a sinusoidal bed.
In steady state, the sliding motion is parallel to the mean bed, so that

Using s* ≪ 1, we get (1 — s*) cos β + s* ~ cos β. We can then simplify Equation (7) by using ![]() which holds at water pressures close to the critical pressure. Equation (7) thus becomes
which holds at water pressures close to the critical pressure. Equation (7) thus becomes

This approximate equation is valid for any periodic bed at high water pressures, β is the maximum slope of the stoss faces of the bed undulations. These undulations do not have to be sinusoidal, s* is a function of the water pressure with ![]()
In the special case of a sinusoidal bed, the function s*(p)w) can be found. Equation (16) of Schweizer and Iken (1992) provides the required relationship:

Their s is the so-called bed-separation parameter and relates to our s* by s* = 1 — s. They obtained their equation in a fashion similar to Reference LliboutryLliboutry (1968) but they made a different assumption on the location of the separated zone. They assumed that the separated zone is centered at the inflection point on the lee face of the sinusoidal bump. This assumption applies during the transient phase of the beginning of cavity growth and, if the ice is almost fully separated, also for fully developed, steady cavities.
s* can now be calculated by using the assumption of a small contact area s* ≪ 1. This allows the expansion of sine and cosine in Equation (10) using a Taylor series. Carrying this out yields:

For a sinusoidal bed,

Thus, as s*→0, the water pressure, pw. approaches the critical pressure, pc, as required.
From Equation (11), we find:

Replacing this in Equation (9), we obtain

Furthermore,

This finally gives

Discussion
Equation (16) shows the expected instability as the water pressure approaches the critical pressure It also preserves the Tn dependency of the sliding velocity that is typical of any sliding law that describes sliding over hard bedrock in the absence of regelalion. A rather appealing fact is that the sliding velocity shows the same dependency on the roughness a/l as in previously derived sliding laws (Reference KambKamb, 1970; Reference FowlerFowler, 1979, Gudmundsson, 1994). This was somewhat unexpected, because the above-mentioned authors did a detailed analysis of sliding over bedrock without cavity formation.
Sliding instabilities at pressures below overburden, as predicted here, have not been observed. The simplifying assumption of a sinusoidal bed does not explain this, since the existence of the critical pressure does not depend on that assumption. Also, it is highly unlikely to find many places with stoss faces perpendicular to the mean bed (β = 90°), which would yield pc = p0. Observations of the glacier bed in front of the present-day terminus of Findelengletschcr, for example, show a somewhat smooth bed (Reference Iken and BindschadlerIken and Bindschadler, 1986). At the few places where the stoss faces are perpendicular to the mean bed, a large proportion of the shear stress should be concentrated once the critical pressure is reached and thus accelerated motion should still occur.
We believe that assumption (iv) (all the cavities are at the same water pressure) is the major simplification. Following a recent paper (Reference IkenIken and Truffer, 1997), we argue that there are isolated cavities beneath Findelengletscher that would prevent such an instability.
Conclusion
An approximate sliding law, valid for a sinusoidal bed in the case of extensive bed separation and other idealized conditions, has been derived from a force budget. An important feature of this law, not included in other sliding laws, is the factor (pc-pw)−(n-1)/2. This factor accounts for the instability of sliding that should occur when the subglacial water pressure, pw, approaches the critical value, pc. The dependence of the sliding velocity on bed roughness (amplitude/wavelength), on wavelength and on basal shear stress is the same as for sliding over a sinusoidal bed without bed separation.
Acknowledgements
We thank K.Echelmeyer for reading the manuscript carefully and helping to improve it, and an anonymous reviewer for critical comments.


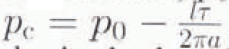 , where
, where 
