1. Introduction
Iceberg calving plays a key role in glacier dynamics, and hence in how tidewater glaciers and ice sheets respond to climate change, thereby impacting predictions of sea-level rise in the future (Reference Van der VeenVan der Veen, 1997; Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2003; Reference Benn, Warren and MottramBenn and others, 2007a; Reference Nick, Vieli, Howat and JoughinNick and others, 2009). So far, the mechanisms underlying the calving dynamics are only partly understood. To summarize the potential controls affecting iceberg calving, Reference Benn, Warren and MottramBenn and others (2007a) proposed the following classification: ‘first-order controls’ determining the position of the glacier terminus, ‘second-order controls’ responsible for the calving of individual icebergs, and ‘third-order controls’ related to the calving of submarine icebergs. The first-order control on calving is the strain rate resulting from spatial variations in the glacier velocity, responsible for the opening of crevasses. Crevasse formation is reinforced by the presence of liquid water, either from surface melt or rain events. Second-order controls are processes weakening the glacier terminus and favoring fracture, such as the presence of force imbalances at the glacier terminus resulting from the margin geometry, undercutting of ice and torque due to buoyancy. Third-order controls trigger submarine iceberg calving by processes such as the formation of basal crevasses, tides and buoyancy.
The majority of previous studies describe calving by means of macroscopic variables, such as the overall calving rate (calving speed), i.e. the total ice loss at the glacier terminus within rather long time intervals. Corresponding models (‘calving laws’) relate the dynamics of the calving speed to parameters such as the water depth (Reference Brown, Meier and PostBrown and others, 1982; Reference Oerlemans, Jania and KolondraOerlemans and others, 2011), the height-above-buoyancy (Reference Van der VeenVan der Veen, 1996; Reference Vieli, Funk and BlatterVieli and others, 2001, 2002), the penetration of surface and basal crevasses arising from the longitudinal strain near the calving terminus and surface melt (Reference Benn, Hulton and MottramBenn and others, 2007b; Reference Nick, Van der Veen, Vieli and BennNick and others, 2010; Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others, 2010) and more general glacier characteristics, such as the ice thickness, the thickness gradient, the strain rate, the mass-balance rate and backward melting of the terminus (Reference Amundson and TrufferAmundson and Truffer, 2010).
To date, only a few studies have been dedicated to a description of calving dynamics at the level of individual calving events. Continuous monitoring of individual events directly at the glacier terminus is challenging; consequently, data are sparse. Previous studies of calving-event statistics were based on occasional or discontinuous observations of calving events (Reference WashburnWashburn, 1936; Reference Warren, Glasser, Harrison, Winchester, Kerr and RiveraWarren and others, 1995; Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2003), or on indirect measurements (e.g. event sizes obtained from icebergs floating in the sea (Reference Budd, Jacka and MorganBudd and others, 1980; Reference OrheimOrheim, 1985; Reference WadhamsWadhams, 1988) or from seismic activity (Reference O’Neel, Larsen, Rupert and HansenO’Neel and others, 2010)). The available data indicate that event sizes are highly variable and broadly distributed (e.g. Reference BahrBahr, 1995; Reference O’Neel, Larsen, Rupert and HansenO’Neel and others, 2010). However, distributions of event sizes obtained from floating icebergs in the sea are likely to be biased, due to melting and disintegration (Reference NeshybaNeshyba, 1980; Reference BahrBahr, 1995). Seismic measurements can only detect large calving events reliably (Reference Köhler, Chapuis, Nuth, Kohler and WeidleKöhler and others, 2012). In addition, estimating calving-event sizes (ice volume) from seismic-event magnitudes is problematic, unless the relation between these two quantities is clearly established (e.g. through calibration by means of direct visual observations; Reference Köhler, Chapuis, Nuth, Kohler and WeidleKöhler and others, 2012). Hence, the resulting size distributions may be biased. In principle, calving activity at the single-event scale could be monitored by means of repeat photography (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2003), laser scanning or ground-based radar (Reference Chapuis, Rolstad and NorlandChapuis and others, 2010). So far, however, no such data have been published. Here we present single-event data obtained from continuous visual observations directly at the termini of two tidewater glaciers on Svalbard. Our data confirm that both the sizes of individual calving events and the time intervals between consecutive events are broadly distributed.
So far, the mechanisms underlying this calving variability remain unknown. It is unclear whether it reflects variability in external conditions (e.g. temperature or tides) or whether it is generated by the internal calving dynamics itself. Fluctuations in external conditions can hardly be controlled in nature. Disentangling these two potential sources of variability therefore requires a model of the calving process. A description of the size and timing of individual calving events is beyond the macroscopic continuum models, which focus on the overall calving rate (see above). Reference BahrBahr (1995), Reference Amundson and TrufferAmundson and Truffer (2010) and Reference BassisBassis (2011) proposed models accounting for the discreteness of calving. In the model of Reference Amundson and TrufferAmundson and Truffer (2010), calving events are triggered when the terminus thickness decreases to some critical value. According to this model, the event sizes and inter-event intervals are fixed for constant model parameters. Variability in event sizes and intervals can only result from fluctuations (e.g. seasonal variations) in these parameters. Reference BassisBassis (2011) describes the motion of the glacier terminus in one dimension as a stochastic process. In Reference BahrBahr (1995), calving is modeled as a percolation process in a two-dimensional (2-D) lattice representing a region close to the glacier terminus. In this model, microfractures are randomly and independently generated, according to some cracking probability. Calving events occur whenever a section of ice is surrounded by a cluster of connected microfractures. In this model, calving in one region of the model glacier has no effect on the state of the rest of the glacier. Both the model of Reference BahrBahr (1995) and that of Reference BassisBassis (2011) are inherently stochastic. In our study, we propose an alternative calving model, focusing on the mutual interplay between calving and the destabilization of the local neighborhood of the calving region. Although the calving dynamics of this model is fully deterministic, it generates broad distributions of event sizes and inter-event interval distributions which are consistent with the field data, even under stationary conditions.
Ultimately, breaking of ice, formation of fractures (crevasses) and, therefore, calving are consequences of internal ice stress (Reference Benn, Warren and MottramBenn and others,2007a). Several mechanisms contribute to the build-up of stress at the glacier terminus (e.g. glacier-velocity gradients, buoyancy, tides or changes in the glacier-terminus geometry due to calving itself). The model proposed in this study describes the interplay between internal ice stress and calving as a positive-feedback loop: the glacier calves if the internal ice stress exceeds a critical value. The detachment of ice leads to an increase in stress in the neighborhood of the calving region, mainly due to a loss of buttress (i.e. a reduction in physical support), but also as a consequence of a reduction in ice burden pressure, increase in buoyancy and terminus acceleration. This increase in ice stress destabilizes the neighborhood of the calving region, i.e. increases the likelihood of calving. In our model, the calving-induced change in ice stress is captured by a parameter, the calving susceptibility. We show that the positive-feedback loop between calving and terminus destabilization alone is sufficient to explain the large variability of iceberg sizes and inter-event intervals observed in the field data. In the model, all other stress contributors are treated as ‘external stress’ or are described by parameters. Keeping these parameters constant enables us to study the glacier dynamics under (ideal) stationary conditions.
The paper is organized as follows: we first describe the acquisition of the field data, the calving model and the data analysis (Section 2). We then present the event-size and interval distributions obtained from the field data and show that they are reproduced by the calving model (Section 3.1). The model predicts a large variability in the calving process even under stationary external conditions. This is supported by the field data showing that the shape of the size and interval distributions is not affected by registered fluctuations in climatic conditions (Section 3.2). Next, we discuss a prediction of the model which may be of significance for judging the stability of a glacier: the model glacier exhibits a critical point at which it enters a regime of ongoing self-sustained calving (Section 3.3), a regime which may be related to observations of rapid glacier retreats. Finally, we demonstrate that the calving model is consistent with the field data, in the sense that the size of future calving events is barely predictable from past events (Section 3.4). In the last section (Section 4), we summarize and discuss the consequences of our work, embed the results into the literature and point out limitations and possible extensions.
2. Methods
2.1. Acquisition of field data
2.1.1. Study regions
Calving activity was monitored at two tidewater glaciers on Svalbard: Kronebreen and Sveabreen. Kronebreen is a grounded, polythermal tidewater glacier, located at 78053’ N, 12030’ E, ~ 14 km southeast of Ny-Ålesund, western Spitsbergen (Fig. 1a). It is one of the fastest tidewater glaciers on Svalbard, with an average terminus velocity between 2.5 and 3.5 m d−1 during the summer months (Reference Rolstad and NorlandRolstad and Norland, 2009). Calving activity was monitored over a 4 day (26 August 2008, 19:00 to 1 September 2008, 05:11 UT) and a 12 day period (14 August 2009, 00:00 to 26 August 2009, 16:00 UT). At the end of August 2008, the terminal ice cliff had an elevation between 5 and 60 m (Reference Chapuis, Rolstad and NorlandChapuis and others, 2010). About 90% of the glacier terminus was visible from the observation camp, located ~ 1.5 km west of the glacier terminus (white triangle in Fig. 1a). The second glacier, Sveabreen, is a 30 km long, grounded tidewater glacier located at 78033’ N, 14020’ E, terminating in the northern part of Isfjorden (Fig. 1b). The observation of Sveabreen was part of a Youth Expedition program with 45 participants, lasting from 17 July 2010, 14:40 to 21 July 2010, 15:00 UT. The camp was located~ 500–700 m from the glacier terminus and offered an unobstructed view (white triangle in Fig. 1b).

Fig. 1. Aerial pictures of (a) Kronebreen and (b) Sveabreen taken in August 2009 and August 2010, respectively. Locations of the observation camps and the time-lapse camera are marked by triangles and the star, respectively. Inset: map of Svalbard showing the location of the two glaciers.
2.1.2. Perceived event sizes and inter-event intervals
Calving activity was monitored by means of direct visual (and auditory) inspection of the glacier termini using human observers. At both Kronebreen and Sveabreen, midnight sun lasts from 18 April to 24 August. Hence, calving activity could be monitored continuously (day and night). Groups of two or three observers worked in shifts. Note that, despite multiple observers, each calving event was registered only once. For each calving event, we registered the type (avalanche, block slump, column drop, column rotation, submarine event; Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2003; Reference Chapuis, Rolstad and NorlandChapuis and others, 2010), location, time and perceived size. For the data analysis, we did not distinguish between different event types. Due to delays between the occurrence of events and their registration by the human observers, we assign a temporal precision of ± 1 min to the inter-event intervals, τ, the time between two consecutive events. Following the semi-quantitative approach introduced by Reference Warren, Glasser, Harrison, Winchester, Kerr and RiveraWarren and others (1995), we monitored the perceived size,Ψ∈{1, 2, … .}, of each calving iceberg on an integer scale (Reference O’Neel, Echelmeyer and MotykaO’Neel and others, 2003). The smallest observable events (Ψ=1) correspond to icebergs with a volume of ~ 10 m3, and the largest (Ψ= 11) to >105 m3 (collapse of about one-fifth of the glacier terminus). During common observation periods, the perceived event sizes, Ψ, registered by different observers could be compared. Based on these data, the error (variability) in Ψ is estimated as ± 1.
2.1.3. Mapping perceived event sizes to iceberg volumes
The perceived iceberg sizes, Ψ, were mapped to the actual iceberg volumes, μ, by means of photogrammetry: repeat photographs were automatically taken at 3 s intervals from a fixed location (star in Fig. 1) using Harbotronics time-lapse cameras (Reference Chapuis, Rolstad and NorlandChapuis and others, 2010, and references therein). In the resulting data, we identified 18 calving events which were simultaneously registered by human observers. The approximate volume, μ, of each event was obtained from the estimated iceberg dimensions, and compared with the perceived size, Ψ (Fig. 2). The relation between μ and Ψ is well fitted by a power law (dashed line in Fig. 2; correlation coefficient c = 0: 68 in double-logarithmic representation):
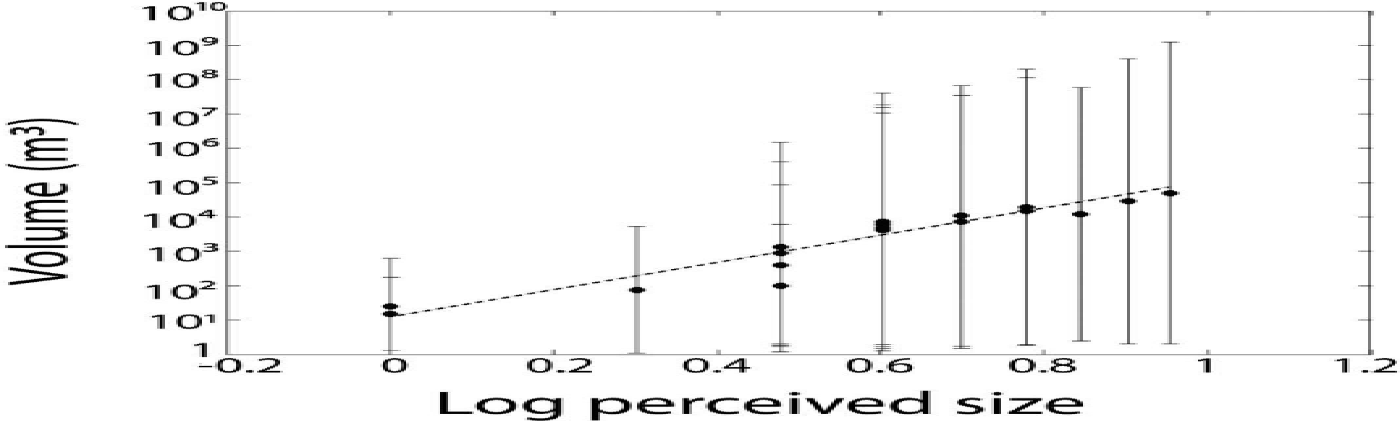
Fig. 2. Dependence of measured iceberg volume, μ, on perceived iceberg size, Ψ, (log-log scale) for 18 individual calving events (symbols). Error bars depict estimated volume measurement errors. The dotted line represents the best power-law fit, Eqn (1) (linear fit in log-log representation).
Note that the empirical power-law model, Eqn (1), is consistent with psychophysical findings (Stevens’ power law; Reference StevensStevens, 1957). Using Eqn (1), we converted the perceived iceberg sizes, Ψ, for all the visually monitored events to an estimated volume, μ (m3).
2.2. Calving model
2.2.1. Overview
In our calving model, the glacier terminus is described as a 2-D, discretized rectangular plane, subdivided into cells (Fig. 3c). Each cell corresponds to a unit volume of ice. The state of a cell is characterized by its internal ice stress. If this stress exceeds a critical level, the ice breaks, the cell ‘calves’ and its stress is reset to zero (Fig. 3a). Calving of a cell increases the stress in neighboring cells (Fig. 3c), as a consequence of a loss of buttress, a reduction in ice burden pressure, an increase in buoyancy and terminus acceleration (e.g. Reference Benn, Warren and MottramBenn and others, 2007a, and references therein). Hence, initial calving of individual cells can trigger calving avalanches involving larger regions of the glacier terminus. We probe the model glacier by applying small perturbations (small stress increments) to randomly selected, individual cells. The total number of cells participating in an avalanche triggered by a single perturbation defines the ‘event size’, μ. The time (number of perturbations) between two consecutive events of nonzero size corresponds to the ‘inter-event interval’, τ. In the following, the model components are described in detail.
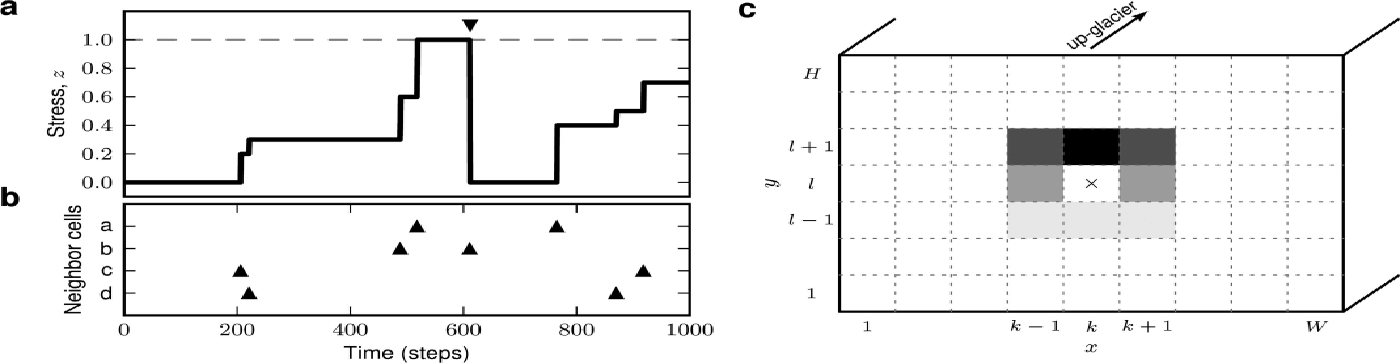
Fig. 3. Sketch of the calving model. (a) Time evolution of internal ice stress, z, in an individual cell. Calving of neighboring cells or external perturbations (triangles shown in (b)) cause jumps in ice stress, z. Crossing of critical stress, z = 1 (dashed horizontal line), leads to calving (down-triangle marker) and reset of stress level to z = 0. (c) Glacier terminus (as seen from the sea/fjord; width W, height H) subdivided into WH cells. Calving of cell {kl} (cross) leads to stress increments (gray coded) in neighboring cells (depending on relative cell position).
2.2.2. Model geometry
The calving model focuses on the calving dynamics at the glacier terminus. For simplicity, the terminus is described as a 2-D rectangular plane of width W and height H. The terminus is discretized, i.e. subdivided into WH cells with coordinates {x, y|x = 1, …, W; y = 1, …, H} (y = 0 and y = H correspond to the sea level and the height of the glacier terminus above sea level, respectively; Fig. 3c). Each cell represents a unit volume of ice. Note that the model neglects the third spatial dimension perpendicular to the terminus plane.
2.2.3. Stress dynamics and calving
The internal ice stress in a cell at position {xy} at time t is described by a scalar variable, zxy (t) (Fig. 3a). The cell calves at time ti xy if its internal stress exceeds a critical value of z crit = 1 (‘yield stress’; e.g. Reference Benn, Warren and MottramBenn and others, 2007a, and references therein), i.e. if zxy (ti xy ) > 1 (triangle in Fig. 3a). The cell’s calving activity can be described mathematically as a sequence of calving times, {ti xy |i = 1, 2, …}, or, more conveniently, as a sum of delta pulses, sxy (t)=Ʃiδ(t-ti xy) (triangles in Fig. 3a and b). Once the cell at position {xy} has calved, it is assumed to be replaced by a ‘fresh’ cell representing ice in a deeper layer. In the model, this replacement is implemented by instantaneously resetting the stress at position {xy} to zero (triangle in Fig. 3a). Note that the geometry of the model (see above) is not altered by calving. We assume that the dynamics of the internal ice stress, zxy (t), represents a jump process which is driven by calving of neighboring cells and external perturbations (triangles in Fig. 3b). Mathematically, the (subthreshold, for zxy ≤ 1) stress dynamics can be described by
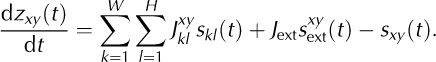
The left-hand side of Eqn (2) denotes the change in stress at time t (temporal derivative). The right-hand side (rhs) describes different types of inputs to the target cell, {xy}. In the absence of these inputs (i.e. if the rhs is zero), the stress level, zxy , remains constant. The first term on the rhs corresponds to the stress build-up due to calving in neighboring cells: calving of cell {kl} at time t leads to an instantaneous jump in zxy with amplitude Jxy kl (Fig. 3a–c; see Section 2.2.4). The second term represents stress increments as a result of external perturbations, sxy ext(t), with amplitude J ext. For simplicity, we assume that these external perturbations are punctual events in time (delta pulses), i.e. sxy ext(t) = Ʃ i δ(t – ti ext, xy ). The last term on the rhs of Eqn (2) captures the stress reset after calving of cell {xy} (as described above) and is treated as a negative input here. Note that the single-cell calving model described here is identical to the ‘perfect integrate-and-fire model’ which is widely used to study systems of pulse-coupled threshold elements such as networks of nerve cells (Reference LapicqueLapicque, 1907; Reference TuckwellTuckwell, 1988) or sand piles (Reference Bak, Tang and WiesenfeldBak and others, 1987, Reference Bak, Tang and Wiesenfeld1988) and to investigate the dynamics of earthquakes (Reference Herz and HopfieldHerz and Hopfield, 1995).
2.2.4. Interactions between cells
Calving of a cell at position {kl} leads to a destabilization of its local neighborhood, mainly caused by a loss of buttress, but also due to local increases in buoyancy and changes in terminus velocity triggered by calving. As a consequence, the stress level in neighboring cells, {xy}, is increased (first term on rhs of Eqn (2)). For simplicity, we assume that the interaction, Jxy kl = J (x – k, y – l), between cells {kl} and {xy} depends only on the horizontal and vertical distances p = x – k and q = y – l, respectively. Further, we restrict the model to excitatory (positive) nearest-neighbor interactions without self-coupling, i.e.
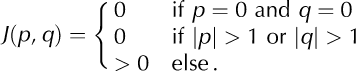
For the results reported in Section 3, we use an asymmetrical interaction kernel (Fig. 3c)
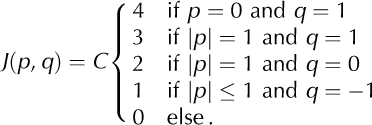
Here C is a normalization constant. The asymmetry in the vertical direction reflects the fact that cells above the calving cell will likely experience a larger stress increment than those below, due to gravity. To test whether the dynamics of the model critically depends on the specific choice of the interaction-kernel shape we also consider symmetrical kernels
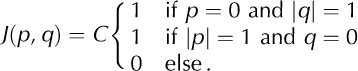
Qualitatively, the results for symmetrical and asymmetrical interaction kernels are the same (not shown here). Note that, with the symmetrical kernel in Eqn (5), our calving model is (essentially) identical to the sand-pile model of Reference Bak, Tang and WiesenfeldBak and others (1987, Reference Bak, Tang and Wiesenfeld1988). (In the model of Bak and others the ‘stress’, z, is reset by a fixed amount after ‘calving’, whereas we consider a reset to a fixed value, z = 0.)
To study the dependence of the calving dynamics on the coupling between cells, we consider the total ‘calving susceptibility’, w =ƩpƩqj(p,q), as a main parameter of the model. It characterizes the overall effect of a calving cell on the ice stress in its local neighborhood. An increase in the susceptibility, w, corresponds to a ‘destabilization’ of the glacier terminus. Note that w is measured in units of the critical stress, z crit; an increase in w can therefore also be interpreted as a decrease in z crit. To study the effect of ice susceptibility and/or yield stress, it is therefore sufficient to vary w and keep z crit = 1 constant. Both ice susceptibility and yield stress are determined by external factors (temperature, glacier velocity, buoyancy, glacier thickness, etc.). An increase in temperature, for example, lowers the yield stress (Reference Benn, Warren and MottramBenn and others, 2007a) and, thus, leads to an increase in the susceptibility, w.
The calving susceptibility, w, plays a key role in the dynamics of the calving model. To illustrate this, let us assume that the states, zxy (t), of the cells are uniformly distributed in the interval [0, 1] (across the ensemble of all cells). Calving of some cell, {kl}, at time t will inevitably trigger calving in any adjacent cell, {xy}, with zxy (t) > 1 – Jxy kl . With the above assumption, the probability of a cell, {xy}, fulfilling this condition is Jxy kl . The total number of cells calving in response to a calving cell is, on average, given by the sum Ʃ{xy} Jxy kl=w over all interaction strengths, i.e. by the calving susceptibility. Therefore, the calving susceptibility, w, can be interpreted as the gain in the total number of calving cells: if w < 1, calving activity will quickly die out; if w > 1, the total number of calving cells tends to grow in time; for w = 1, the system is balanced, in the sense that the average total number of calving cells remains approximately constant. Strictly speaking, this holds only under the above assumption of a uniform state distribution. As illustrated in Figure 6b and c, the cell states are indeed widely distributed over the entire stress interval, [0, 1]. Therefore, we may expect that w = 1 marks a transition point for the dynamics of the model. In fact, as shown in Section 3.1, the variability in calving-event sizes increases substantially at w ~ 1 (Reference Shew and PlenzShew and Plenz, 2013).
2.2.5. Experimental protocol
Due to the interactions between cells described above, calving of individual cells may trigger calving in neighboring cells, thereby causing calving avalanches. At the beginning of each experiment, the internal ice stress of each cell was initialized by a random number drawn from a uniform distribution between 0 and 1.1. On average, 10% of the cells were therefore above the critical stress, z crit = 1, and started calving immediately. In general, this initial calving stopped after some time (see, however, Section 3.3). After this warm-up period, we performed a sequence of perturbation experiments: in each trial m = 1, …, M, a single cell, {kl}, was randomly chosen and perturbed by a weak delta pulse skl ext(t) = δ (t) of amplitude J ext = 0: 1 (at the beginning of each trial, time was reset to t = 0). The trial was finished when the calving activity in response to the perturbation had stopped. We define the number of cells calving in a single trial as the ‘event size’, μ. The difference, m – u, between the id’s of two subsequent successful trials u and m > u (m, u ∈ [1, M]), i.e. trials with μ > 0, defines the ‘inter-event interval’, τ. Examples of calving activity in individual trials are shown in Figure 6.
2.2.6. Model parameters
The model parameters are summarized in Table 1.
Table 1. Model parameters. Curly brackets {} represent parameter ranges

2.2.7. Simulation details
The model dynamics was evaluated numerically using the neural-network simulator NEST (Reference Gewaltig and DiesmannGewaltig and Diesmann, 2007; www.nest-initiative.org), which was developed and optimized to simulate large systems of pulse-coupled elements. Simulations were performed in discrete time, t = 0, 1, 2, …. Cell states were updated synchronously, i.e. calving activity at time t increments the stress in neighboring cells at time t + 1.
2.3. Data analysis
In the following, we describe the characterization of the marginal distributions and autocorrelations of event sizes and inter-event intervals. Field and model data were analyzed using identical methods. Similarly, we applied identical tools to the event sizes, μ, and the inter-event intervals, τ. Unless stated otherwise, we will therefore not distinguish between μ and τ in this subsection, and use X as a placeholder.
2.3.1. Distributions of sizes and intervals
The overall characteristics of the distribution of data points, Xi (i = 1, …, n; n is sample size), are given by its mean, standard deviation, SD, minimum and maximum, and the coefficient of variation, CV = SD/ mean (Table 2). In the case of the inter-event intervals, the CV provides a measure of the regularity of the calving process: while CV = 0 corresponds to a perfectly regular process with a delta-shaped interval distribution (clock), CV = 1 is characteristic of a process with an exponential interval distribution (e.g. a Poisson point process (Reference CoxCox, 1962)). Histograms of the data on a logarithmic scale (relative frequency: number of observations within an interval [log10 (X), log10 (ΔX)] normalized by n) are used as a graphical illustration of the entire distributions. As shown in Figures 5b–g, 7a and d and 9 (symbols), the empirical distributions obtained in this way are broad, and resemble power-law or exponential distributions. Note, however, that such histograms, obtained by binning of finite datasets, are generally biased and, therefore, not appropriate for a quantitative analysis (Reference Clauset, Shalizi and NewmanClauset and others, 2009). Here we applied maximum-likelihood (ML) methods (Reference Clauset, Shalizi and NewmanClauset and others, 2009) to quantify the extent to which the field and model data, X, can be explained by an exponential or a power-law distribution:
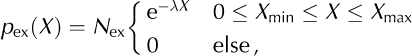
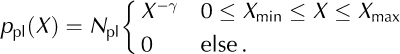
Table 2. Overview of the three field datasets with event-size and interval statistics

The cut-offs were set to the observed minimum and maximum, respectively: X min = min i (Xi ), X max = max i (Xi ). The prefactors, N pl and N ex, are normalization constants. The exponents, λ and γ, were obtained by maximizing the log-likelihoods, l ex/ pl = E i [log(p ex/ pl(Xi )), for the two model distributions. Here E i […]=1/nƩn i=1 … denotes the average across the ensemble of data points. The quality of the ML fits (goodness-of-fit test) was evaluated as described by Reference Clauset, Shalizi and NewmanClauset and others (2009), using surrogate data and Kolmogorov– Smirnov statistics. The resulting p –values indicate how well the data can be explained by the model distributions, p ex(X) or p pl(X). The log-likelihood ratio, R = l pl = l ex, the difference between the maximum log-likelihoods, is used to judge which of the two hypotheses, the power-law or the exponential model, fits the data better. R > 0 indicates that the power-law model, p pl(X), is superior (and the contrary for R < 0). The variance of R, estimated as E i [(Ri – R)2] with Ri = log(p pl(Xi )) – log(p ex(Xi )) for the best-fit distributions, was used to test whether the measured log-likelihood ratio, R, differs significantly from zero (Reference Clauset, Shalizi and NewmanClauset and others, 2009).
2.3.2. Autocorrelations
To investigate whether calving event sizes and intervals are informative about future events, we calculated the normalized autocorrelations (Fig. 11)
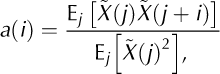
With
![]()
2.3.3. Software
The data analysis was performed using Python (http://www.python.org) in combination with NumPy (http://numpy.scipy.org) and SciPy (http://scipy.org). Results were plotted using matplotlib (http://matplotlib.sourceforge.net).
3. Results
Calving at the termini of tidewater glaciers often occurs as a sequence of events, thereby showing the characteristics of avalanches: an initial detachment of small ice blocks can cascade to events of arbitrary size (Fig. 4). Here we propose that the underlying dynamics can be understood as a result of the mutual interplay between calving and the destabilization of the local neighborhood of the calving region. By means of a simple calving model (Section 2.2), we show that this mechanism is sufficient to understand the variability in event sizes and inter-event intervals observed in the field data (Section 3.1). Fluctuations in external parameters may additionally contribute to the calving variability but are not required to explain the data. This is confirmed by our observation that changes in air temperature and tides do not affect the shape of the size and interval distributions obtained from the field data (Section 3.2). The simple calving model enables us to study the effect of glacier parameters on the distributions of event sizes and intervals in a controlled manner. An increase in the calving susceptibility leads to broader event-size distributions. At a critical susceptibility, the model glacier undergoes a transition to a regime where a small perturbation leads to ongoing calving activity (Section 3.3). Finally, we show that the simple calving model is consistent with the field data, in the sense that the size of future calving events is not correlated with the size of past events. Predicting event sizes from past events is thus difficult, if not impossible (Section 3.4).

Fig. 4. Typical calving sequence observed on 16 August 2009, 21:46 UT, at Kronebreen. The detachment of small ice blocks (b, c) triggers a large column drop, with the entire height of the terminus collapsing vertically (d–g), followed by large column-rotation events with blocks of ice rotating during their fall (h–j). Time distance between consecutive images is 3 s. Black arrow and ellipses mark location of individual calving events.
3.1. Variability of event sizes and inter-event intervals
We analyzed data obtained from Kronebreen and Sveabreen during three continuous observation periods with >7000 calving events in total. The longest observation period lasted 12 days with 5868 events (Fig. 5a). An overview of the three datasets and the basic event-size and interval statistics is provided in Table 2.

Fig. 5. Field data. (a) Example time series for 12 observation days at Kronebreen (2009). Each bar represents a calving event of size μ (log scale). (b–g) Distributions (log-log scale) of iceberg sizes, μ, (b–d) and inter-event intervals, τ, (e–g) for Kronebreen 2008 (b, e), 2009 (c, f) and Sveabreen 2010 (d, g). Field data (symbols), best-fit power-law (solid lines; decay exponents, γμ, γτ ) and exponential distributions (dashed curves; decay exponents λμ, λτ ). R represents corresponding log-likelihood ratio.
The sizes, μ, of monitored events are highly variable. They extend over four orders of magnitude, from ~ 10 m3 up to >105 m3 (symbols in Fig. 5b–d). The event-size coefficient of variation, CV, varies between 6.2 and 8.2; the standard deviations are substantially larger than the mean values (542–1512 m3). The distributions of event sizes exhibit long tails and resemble power laws, Eqn (7). Maximum-likelihood (ML) fitting yields power-law exponents, γμ , between 1.7 and 2 (solid gray lines in Fig. 5b–d). Note, however, that the p –values of the goodness-of-fit test (Section 2.3) are, in all cases, very small, indicating that the power-law model does not perfectly explain the event sizes. Nevertheless, the power-law model, Eqn (7), fits the event sizes, μ, better than the exponential model, Eqn (6) (dashed curves in Fig. 5b–d); the log-likelihood ratios, R, are in all cases significantly greater than zero (R = 2.3–14).
The inter-event intervals, τ, span more than two orders of magnitude (1 min to >400 min; symbols in Fig. 5e–g). The standard deviations exceed the mean durations between two events (3–17 min) by a factor of CV = 1.5–1.9. Hence, the calving process is highly irregular; substantially more irregular than a Poisson point process with exponential interval distribution (CV = 1; Reference CoxCox, 1962). The interval distributions have a longer tail than predicted by the exponential model, Eqn (6) (dashed curves in Fig. 5e–g), but fall off more rapidly than the power-law model, Eqn (7) (solid gray lines in Fig. 5e–g). The log-likelihood ratios R ≈ 0 confirm that the inter-event intervals τ are neither exponentially nor power-law distributed.
The simple calving model reproduces well the characteristics of the event-size and interval distributions obtained from the field data. An example time series generated by the calving model is depicted in Figure 6a for a susceptibility of w = 1: 3. Small random perturbations of the model glacier lead to responses with broadly distributed magnitudes. In most cases, there is no response (μ = 0). Small events are frequently triggered (see example in Fig. 6b, d and f), whereas large events are rare (see example in Fig. 6c, e and g). As in the field data, the distributions of event sizes, μ, generated by the calving model resemble power-law distributions (Fig. 7a). The width of the size distribution increases with the calving susceptibility, w, (Fig. 7b) while the power-law exponent, γμ , decreases and approaches 1 for w = 1: 3 (solid curve in Fig. 7c). Log-likelihood ratios, R, are always positive and increase with w (data not shown), indicating that the power-law model, Eqn (7), fits the data better than the exponential model, Eqn (6). For w = 1: 3, the size distribution spans about six orders of magnitude (μ = 1, …, 106). Note that the maximum event size can exceed the system size, WH (dashed vertical lines in Fig. 7a and b), as a single cell can calve several times during one event (trial).

Fig. 6. Size and duration variability of calving events in response to random external perturbations (model results). (a) Glacier responses (event size μ; log scale) to 1000 consecutive random perturbations. Black square (trial 190) and circle (trial 884) mark events shown in (b, d, f) and (c, e, g), respectively. (b–g) Moderate-size (b, d, f; μ = 15) and large (c, e, g; μ =27 903) calving events in response to punctual random perturbations (perturbation sites indicated by black stars) in trials 190 and 884, respectively. (b, c) Distribution of stress, zxy (gray coded), across the model-glacier terminus after calving response. (d, e) Spatial spread of single-trial calving activity across the model glacier terminus. Gray dots mark cells which have calved. (f, g) Spatio-temporal spread of the events shown in (d, e). id of cell at position (x, y) is Hx + y. Note different scales in (f) and (g). Glacier width W = 200, glacier height H = 50, calving susceptibility w = 1: 3.

Fig. 7. Size (top row) and inter-event interval distributions (bottom row) generated by the calving model. (a, d) Distributions (log-log scale) of iceberg sizes μ (a) and inter-event intervals τ (d) for calving susceptibility w = 1: 25. Simulation results (symbols), best-fit power-law (solid lines) and exponential distributions (dashed curves). (b, e) Dependence of size and interval distributions (log-log scale) on calving susceptibility, w. Solid white curves mark maximum sizes and inter-event intervals. (c, f) Dependence of decay exponents of best-fit power-law (solid curves; γμ, γτ ) and exponential distributions (dotted curves; λμ, λτ ) on calving susceptibility, w. Glacier width W = 400, glacier height H = 100. Vertical dashed lines in (a, b) indicate system size WH = 40 000. Dotted horizontal and vertical lines in (b, e) and (c, f), respectively, mark susceptibility w = 1: 25 used in (a, d). Hatched areas in (b, c, e, f) correspond to regions with ongoing self-sustained calving (Section 3.3).
The inter-event intervals, τ, obtained from the calving model span about two orders of magnitude (Fig. 7d and e). In contrast to the event-size distributions, the width of the interval distribution is independent of the calving susceptibility, w (Fig. 7e). Maximum-likelihood fitting of the power-law, Eqn (7), and the exponential model, Eqn (6), yields exponents, γτ and λτ , which are comparable to those obtained for the field data (Fig. 7f cf. Fig. 5e–g). The log-likelihood ratios, R, are always close to zero (data not shown), again consistent with the field data.
Note that the calving variability arising from the model is not merely a result of the randomness of the external perturbations (Section 2.2.5). Restricting the repeated external perturbations to one and the same cell in the center, {W/ 2, H/ 2}, of the terminus results in slightly narrower but qualitatively similar event-size and interval distributions (data not shown).
3.2. Impact of external parameters
As shown in Section 3.1, the calving model generates broad distributions of event sizes and inter-event intervals, even under perfectly stationary conditions. Fluctuations in external parameters are therefore not required to explain the event-size and interval variability observed in the field data. Here we further support this finding by analyzing the relation between calving activity and fluctuations in air temperature and tides during the observation period. Both tides and temperature can, in principle, affect calving activity. High tides increase buoyant forces, thereby destabilizing the glacier terminus. An increase in temperature lowers the yield stress (Reference Benn, Warren and MottramBenn and others, 2007a) and therefore leads to an increase in the calving susceptibility, w. Hence, one may expect that temperature and tide-level fluctuations lead to changes in the calving-event size and interval statistics, and thereby explain the large variability reported in Section 3.1 (Fig. 5).
Figure 8 depicts the simultaneous time series for event sizes, inter-event intervals, air temperature, change in air temperature and tidal amplitude during the 12 day observation period in 2009 at Kronebreen. Within this sampling period, temperatures varied between _ 0: 8 and 8.80C, tide levels between 14 and 178 cm. Significant correlations between climatic parameters and calving activity are not observed.

Fig. 8. Relationship between calving and external parameters (field data, Reference Rolstad and NorlandKronebreen, 2009). (a) Event sizes, μ (log scale). Individual events (dots) and 4 hour average (black curve). (b) Inter-event intervals, τ (log scale). Individual events (dots) and 8 hour average (black curve). (c) Air temperature (Ny-Ålesund, Norwegian Meteorological Institute). (d) Change in air temperature over 6 hour intervals. (e) Tidal amplitude (Norwegian Mapping Authorities).
To test whether fluctuations in air temperature and tidal amplitude affect the overall shape of the event-size and interval distributions, we grouped the data into high/low temperature/tide intervals. The event-size and interval histograms obtained for each group are indistinguishable (Fig. 9). Hence, the fluctuations in air temperature and tides within the observation period have no effect on the shape of the distributions. They cannot explain the observed eventsize and interval variability. This does not imply that changes in temperature and tides do not affect the calving statistics in general. Long-term observations are required to investigate how larger modulations in temperature and tide levels (e.g. seasonal fluctuations) affect the shape of the event-size and interval distributions (Section 4).

Fig. 9. Distributions of (a) iceberg sizes, μ, and (b) inter-event intervals, τ, for four different combinations of air-temperature and tide ranges (Reference Rolstad and NorlandKronebreen, 2009; log-log scaling): high temperature– high tide (HH), high temperature–low tide (HL), low temperature– high tide (LH), low temperature–low tide (LL). Low/high air-temperature interval: _ 0: 8 to 4.2 /4.2_8.80C. Low/high tide-level interval: 14–92 /92–178 cm.
From the results reported here, we cannot exclude the possibility that fluctuations in other parameters (e.g. changes in glacier velocity or buoyancy) contribute to the size and interval variability. Note, however, that both glacier velocity and buoyancy are affected by calving itself (Reference Benn, Warren and MottramBenn and others, 2007a). They are not purely ‘external’ parameters. In our simple model, the positive-feedback loop between calving and these parameters is abstracted in the form of the (positive) interaction kernel (Section 2.2). Hence, correlations between calving activity and fluctuations in glacier velocity or buoyancy can arise naturally from the local calving dynamics at the glacier terminus.
3.3. Self-sustained calving
For susceptibilities w ≤ 1: 3, small perturbations of the model glacier result in calving responses with finite lifetimes (e.g. Fig. 6f and g). Calving of a single cell can trigger an avalanche which sooner or later fades away and stops. For w > 1: 3, the model glacier enters a new regime, where the avalanche lifetimes seem to diverge (hatched areas in Fig. 7b, c, e and f). We illustrate this by randomly initializing the model glacier such that only a small fraction (1%) of cells is superthreshold (z > 1) at time t = 0 and hence starts calving immediately, simulating the model glacier until this initial calving stops and measuring the corresponding survival time for a broad range of susceptibilities, w = 0: 8, …, 1: 5 (Fig. 10). For w > 1, the survival time quickly increases with w and diverges at about w = 1: 3. Beyond this critical susceptibility, calving never stopped within the maximum simulation time (here 900 time steps). Note that this behavior is robust and does not critically depend on the choice of other model parameters, such as the terminus dimensions (W, H) and the shape of the interaction kernel, Eqn (3). In all cases, we observe a critical susceptibility close to w = 1: 3 (data not shown).

Fig. 10. Survival time of calving activity after random stress initialization (with 1% of the cells being superthreshold, zxy > 1, at time t = 0) as function of calving susceptibility, w. Mean survival time (black circles) and mean ± 2 standard deviations (gray band) for 100 random glacier initializations. Glacier width: W = 400; height: H = 100.
3.4. Predictability
In the field data, the average correlation between the sizes, μj and μj +i , of subsequent events, j and j + i, hardly differs from zero for all i > 0 (Fig. 11a). Hence, predicting future event sizes from past events appears hopeless. This behavior is reproduced by the simple calving model (Fig. 11b). The inter-event intervals, τ, obtained from the field data exhibit a moderate long-lasting correlation which is not observed in the model data (Fig. 11c and d). The reason for this discrepancy between the model and the field data is unclear, but we suspect that it is due to non-stationarities in the field data (Fig. 8b) which are, by construction, absent in the model.
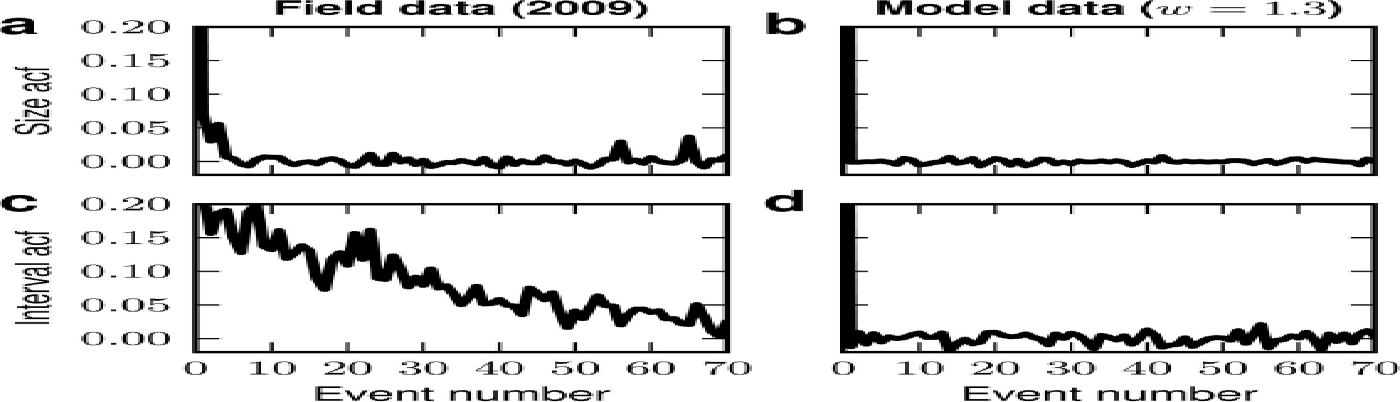
Fig. 11. Autocorrelation function (acf) of (a, b) event sizes and (c, d) inter-event intervals for the field data (a, c) and model data (b, d).
4. Discussion
We have shown that calving-event sizes and inter-event intervals obtained from direct continuous observations at the termini of two tidewater glaciers are highly variable and broadly distributed. We demonstrated that the observed variability can be fully explained by the mutual interplay between calving and the destabilization of the local neighborhood of the calving region. A simple calving model accounting for this interplay reproduces the main characteristics of the event-size and interval statistics: (1) Event-size distributions resemble power laws with long tails spanning several orders of magnitude. (2) Interval distributions are broad but fall off more rapidly than power laws. (3) Correlations between the sizes of subsequent events vanish. We conclude that the observed calving variability is a characteristic feature of calving and is not primarily the result of fluctuating external (e.g. climatic) conditions. Event sizes of all magnitudes have to be expected, even under ideal stationary conditions.
The calving model predicts that the width of the eventsize distribution depends on a parameter, w, representing the calving susceptibility of the glacier terminus: roughly, w measures how prone the glacier is to calve in response to calving. It describes to what extent calving increases the internal ice stress in the neighborhood of the calving region. Alternatively, w may represent the inverse of the yield stress, i.e. the critical stress at which ice breaks. The susceptibility, w, is determined by the properties of the ice and by factors such as temperature, glacier velocity, buoyancy or glacier thickness. In our model, the width of the event-size distribution increases monotonically with w. Therefore, the shape of the size distribution, as, for example, characterized by the power-law exponent, γμ,, may be informative about the stability of the glacier terminus. In contrast to the event-size distributions, the shape of the inter-event interval distribution is insensitive to the susceptibility, w. At a critical susceptibility, w crit, the model predicts an abrupt transition of the glacier to a new regime, characterized by ongoing, self-sustained calving activity. Observations of rapid glacier retreats (Reference PfefferPfeffer, 2007; Reference Briner, Bini and AndersonBriner and others, 2009; Reference Motyka, Truffer, Fahnestock, Mortensen, Rysgaard and HowatMotyka and others, 2011) may be explained by these supercritical dynamics (see also Reference Amundson and TrufferAmundson and Truffer, 2010). In the model, the power-law exponent, γμ , is close to 1 as the susceptibility approaches the critical value, w crit (solid curve in Fig. 7c). We found that this observation does not critically depend on the choice of the model parameters (glacier dimensions, shape of the interaction kernel, perturbation protocol; data not shown here). This suggests that the power-law exponent, γμ , may serve as an indicator of a glacier’s proximity to the transition point where it starts retreating rapidly. Reference BassisBassis (2011) proposed a similar stability criterion, which depends on various geometric and dynamical near-terminus parameters. In our case, the diagnostics is exclusively based on the distribution of event sizes.
The calving model in this study is inspired by previous work on the emergence of power-law distributions. Power-law-shaped magnitude distributions are abundant in nature. They are found, for example, for earthquake magnitudes (Reference Bak, Christensen, Danon and ScanlonBak and others, 2002; Reference HainzlHainzl, 2003), luminosity of stars (Reference BakBak, 1999), avalanche sizes in sand piles (Reference BakBak, 1999), landslide areas (Reference Guzzetti, Malamud, Turcotte and ReichenbachGuzzetti and others, 2002), subglacial water-pressure pulses (Reference KavanaughKavanaugh, 2009), dislocation avalanches in ice (Reference Richeton, Weiss and LouchetRicheton and others, 2005) and sea-ice fracturing (Reference Rampal, Weiss, Marsan, Lindsay and SternRampal and others, 2008). Reference Bak, Tang and WiesenfeldBak and others (1987) demonstrated that power-law distributions can arise naturally in spatially extended dynamical systems which have evolved into ‘self-organized critical states’, consisting of minimally stable clusters of all length scales. Perturbations can propagate through the system and evoke responses characterized by the absence of spatial and temporal scales (avalanches). The calving model used in the present study is qualitatively similar to the sand-pile model of Reference Bak, Tang and WiesenfeldBak and others (1987). It is therefore not surprising that it predicts power-law shaped event-size distributions. The scientific value of this part of our work consists in mapping the original model by Reference Bak, Tang and WiesenfeldBak and others (1987) to the dynamics of glacier calving and in relating the model parameters to physical measures. Moreover, to our knowledge, this is the first report of the phenomenon of self-sustained ongoing activity in this context.
Several aspects of this work may be subject to criticism and improvement, in particular the data acquisition and the construction of the calving model: direct visual observation by humans is, at present, one of the most reliable methods of monitoring individual calving events in continuous time (Van der Reference Van der VeenVeen, 1997). However, the results are hard to reproduce exactly; due to the sporadic unpredictable nature of calving, it is difficult to capture each event. Different observers may be in different attentive states. Each new observer needs to adjust to a common scale of perceived sizes, Ψ. To minimize the variability in perceived sizes, we arranged test observations where all observers were simultaneously confronted with size estimates (Section 2.1). To confirm our findings on the relation between the shape of the event-size distribution and the state of the glacier, more data are needed from glaciers in different environments (fresh water, floating tongue, ice shelves) and different dynamical states (advancing, stable, retreating). To test our stability criterion, one would need to continuously monitor the same glacier year after year for a few days. Long-term continuous observations or observations in cold months are difficult. Automatic monitoring would therefore be highly desirable. Unfortunately, all available automatic-monitoring methods have limitations. Terrestrial photogrammetry, for example, is limited by the iceberg size, visibility and illumination of the glacier. Iceberg size and type also limit the use of ground-based radar. Reference Chapuis, Rolstad and NorlandChapuis and others (2010) showed that radar could only detect events larger than 150 m3. Remote sensing (optical and radar imagery) has the same limitations as terrestrial photogrammetry. In addition, its low temporal resolution does not allow individual calving events to be registered. Seismic monitoring (Reference O’Neel, Larsen, Rupert and HansenO’Neel and others, 2010) is a very promising technique, but can detect only the largest events (Reference Köhler, Chapuis, Nuth, Kohler and WeidleKöhler and others, 2012). The range of event sizes accessible by seismic methods may, however, be sufficient to estimate power-law exponents. A major problem in studying the statistics of individual calving events is to define what a single event actually is. In the framework of our model, an event is defined as the total response to a single perturbation. In our numerical experiments, a new perturbation is not applied before the response to the previous perturbation has stopped. In nature, however, the glacier terminus may be constantly perturbed (e.g. by the movement of the glacier). Several events may be triggered simultaneously in neighboring regions of the terminus and, hence, overlap both spatially and temporally. The separation of individual events in the field data can therefore be difficult. In consequence, short intervals and small events may be underestimated.
The calving model used in this study is highly minimalistic. It implements the mechanism which we think is essential for an understanding of the calving variability observed in the field data (i.e. a positive-feedback loop between calving and destabilization of the glacier terminus), but neglects a variety of factors. First, the model is 2-D. Stress can only propagate tangentially and not in the third dimension, perpendicular to the terminus. Extending the model to three dimensions is not straightforward, as it is unclear how calving at the terminus affects regions deeper within the ice body. Second, the interaction kernel is restricted to nearest-neighbor interactions. Whether and how calving affects regions more distant from the calving region is unclear. A direct measurement of the interaction kernel in the field is difficult, as it would require monitoring of changes in ice stress in response to individual calving events. Conclusions about the shape of the interaction kernel could be drawn indirectly from the spatial structure of calving avalanches (e.g. obtained by terrestrial photogrammetry). For illustration, consider Figure 6e; the triangular shape of this large event is a direct consequence of the asymmetry of the interaction kernel in Eqn (4) (Fig. 3c). For symmetrical kernels, Eqn (5), we observed that the spatial structure of calving events was, on average, symmetrical (data not shown here). Note, however, that for the main findings of our study, the exact shape of the interaction kernel is not critical. Third, the relationships between the susceptibility, w (the area of the interaction kernel; Section 2.2), and external parameters, such as air temperature, tides, glacier velocity or buoyancy, are unclear. These relationships could be established empirically from a larger dataset obtained from continuous long-term observations of different glaciers in different dynamical states. For each identified set of external parameters, our model could be fitted to the distribution of monitored event sizes, thereby providing an estimate of w. Based on these relationships, the event-size distributions for a new ‘test’ dataset (i.e. for data not used for the fitting procedure) could be predicted by the model and compared with the field-data distributions. Fourth, stress increments in response to calving or external perturbations are instantaneous in the model. In reality, these interactions are likely to be smoother and delayed. Detailed information about this is, however, limited. Fifth, in the absence of calving and external perturbations, internal ice stress in a given model cell is constant. In real ice, stress in a certain volume element may slowly dissipate and decay to zero. We assume that the time constant of this decay is much larger than the time between two (external or internal) perturbations and therefore can be approximated as being infinite. Sixth, external perturbations are modeled as punctual (delta-shaped) events in time and space to characterize the system’s response in a well-defined manner (i.e. to evoke responses without spatio-temporal overlap; see above). In reality, external perturbations are spatially and temporally distributed (e.g. glacier movement, glacier velocity gradients, buoyancy). Finally, the model neglects submarine calving which, in reality, amounts to ~ 13% of the total ice loss at the terminus. One way to account for the submarine dynamics would be to assign different calving susceptibilities to the subaerial and the submarine parts. Our model describes calving at the level of individual events and focuses on a single aspect of calving: the interplay between calving and terminus destabilization. Factors such as air temperature, water depth, height-above-buoyancy, surface melt, ice thickness, thickness gradient, strain rate, mass-balance rate and backward melting of the terminus are included indirectly or lumped together and treated as constant parameters. Previous macroscopic models (Reference Brown, Meier and PostBrown and others, 1982; Reference Van der VeenVan der Veen, 1996; Reference Vieli, Funk and BlatterVieli and others, 2001, Reference Vieli, Jania and Kolondra2002; Reference Benn, Hulton and MottramBenn and others, 2007b; Reference Amundson and TrufferAmundson and Truffer, 2010; Reference Nick, Van der Veen, Vieli and BennNick and others, 2010; Reference Otero, Navarro, Martin, Cuadrado and CorcueraOtero and others, 2010; Reference Oerlemans, Jania and KolondraOerlemans and others, 2011) relate these factors to the overall calving rate. A description of size and timing of individual calving events is beyond the scope of most of these models. Our model could be connected to these models by linking the overall calving rate to the calving susceptibility or the characteristics of external perturbations. The resulting multi-scale model would have the potential to describe the statistics of event sizes and inter-event intervals under more realistic non-stationary conditions. The rationale behind the simplistic approach presented in our study is the opposite: to construct a minimal model which reproduces the main characteristics of the event-size and interval statistics. Disconnecting the glacier terminus from the external world allows us to study calving dynamics under ideal stationary conditions and to demonstrate that the observed calving variability is not primarily a result of fluctuations in external conditions, but can emerge from simple principles governing the dynamics directly at the glacier terminus.
To conclude, we propose that the observed variability of tidewater-glacier calving can result from the calving dynamics at the glacier terminus, even under stationary external conditions. Hence, calving events of all magnitudes have to be expected at any time. At a critical calving susceptibility, the terminus undergoes a phase transition, leading to self-sustained ongoing calving activity. The shape of the eventsize distribution (the power-law exponent) may be used to assess the proximity to this critical point, i.e. the stability of the glacier.
Acknowledgements
We acknowledge support from the Research Council of Norway (IPY-GLACIODYN [project 176076], eVITA [eNEURO], Notur), the Helmholtz Association (HASB and portfolio theme SMHB), the Jülich Aachen Research Alliance (JARA), EU grant 269921 (BrainScaleS) and the Svalbard Science Forum. We thank Cecilie Denby-Rolstad, Nial Peters, Allan Buras, Bas Altrena and Katrin Amby for their help collecting the calving data for Kronebreen. We are grateful to Abigail Morrison, Cecilie Denby-Rolstad and the reviewers for valuable comments on the manuscript.














