Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Connes, Alain
and
Consani, Caterina
2016.
Absolute algebra and Segal's Γ-rings.
Journal of Number Theory,
Vol. 162,
Issue. ,
p.
518.
Connes, Alain
2016.
Open Problems in Mathematics.
p.
225.
TANAKA, Hidekazu
2020.
GAMMA FACTORS OF ZETA FUNCTIONS AS ABSOLUTE ZETA FUNCTIONS.
Kyushu Journal of Mathematics,
Vol. 74,
Issue. 2,
p.
441.
Connes, Alain
and
Consani, Caterina
2021.
Segal’s Gamma rings and universal arithmetic.
The Quarterly Journal of Mathematics,
Vol. 72,
Issue. 1-2,
p.
1.
Blumberg, Andrew
and
Mandell, Michael
2024.
The Strong Künneth Theorem for Topological Periodic Cyclic Homology.
Memoirs of the American Mathematical Society,
Vol. 301,
Issue. 1508,


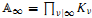 , provides the right theory to obtain, using λ-operations, Serre's archimedean local factors of the complex L-function of
, provides the right theory to obtain, using λ-operations, Serre's archimedean local factors of the complex L-function of 