Article contents
On the algebraic K-theory of truncated polynomial algebras in several variables
Published online by Cambridge University Press: 18 February 2014
Abstract
We consider the algebraic K-theory of a truncated polynomial algebra in several commuting variables, 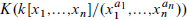 . This naturally leads to a new generalization of the big Witt vectors. If k is a perfect field of positive characteristic we describe the K-theory computation in terms of a cube of these Witt vectors on ℕn. If the characteristic of k does not divide any of the ai we compute the K-groups explicitly. We also compute the K-groups modulo torsion for k = ℤ.
. This naturally leads to a new generalization of the big Witt vectors. If k is a perfect field of positive characteristic we describe the K-theory computation in terms of a cube of these Witt vectors on ℕn. If the characteristic of k does not divide any of the ai we compute the K-groups explicitly. We also compute the K-groups modulo torsion for k = ℤ.
To understand this K-theory spectrum we use the cyclotomic trace map to topological cyclic homology, and write 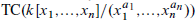 as the iterated homotopy cofiber of an n-cube of spectra, each of which is easier to understand.
as the iterated homotopy cofiber of an n-cube of spectra, each of which is easier to understand.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © ISOPP 2014
References
REFERENCES
1.Angeltveit, Vigleik, Gerhardt, Teena, and Hesselholt, Lars. On the K-theory of truncated polynomial algebras over the integers. J. Topol. 2(2) (2009), 277–294.CrossRefGoogle Scholar
2.Blumberg, Andrew J. and Mandell, Michael A.. Localization theorems in topological Hochschild homology and topological cyclic homology. Geom. Topol. 16(2) (2012), 1053–1120.CrossRefGoogle Scholar
3.Bökstedt, M., Hsiang, W. C., and Madsen, I.. The cyclotomic trace and algebraic K-theory of spaces. Invent. Math. 111(3) (1993), 465–539.CrossRefGoogle Scholar
4.Dress, Andreas W. M. and Siebeneicher, Christian. The Burnside ring of profinite groups and the Witt vector construction. Adv. in Math. 70(1) (1988),87–132.CrossRefGoogle Scholar
5.Dundas, Bjørn Ian. Relative K-theory and topological cyclic homology. Acta Math. 179(2) (1997), 223–242.CrossRefGoogle Scholar
6.Dundas, Bjørn Ian, Goodwillie, Thomas G., and McCarthy, Randy. The local structure of algebraic K-theory, Algebra and Applications 18, Springer, Berlin, 2012.Google Scholar
7.Geisser, Thomas and Hesselholt, Lars. Bi-relative algebraic K-theory and topological cyclic homology. Invent. Math. 166(2) (2006), 359–395.CrossRefGoogle Scholar
8.Hesselholt, Lars. K-theory of truncated polynomial algebras. In Handbook of K-theory 1, 2, pages 71–110. Springer, Berlin, 2005.CrossRefGoogle Scholar
9.Hesselholt, Lars. On the K-theory of the coordinate axes in the plane. Nagoya Math. J. 185 (2007), 93–109.CrossRefGoogle Scholar
10.Hesselholt, Lars and Madsen, Ib. Cyclic polytopes and the K-theory of truncated polynomial algebras. Invent. Math. 130(1) (1997), 73–97.CrossRefGoogle Scholar
11.Hesselholt, Lars and Madsen, Ib. On the K-theory of finite algebras over Witt vectors of perfect fields. Topology 36(1) (1997), 29–101.CrossRefGoogle Scholar
12.Lewis, L. G. Jr., May, J. P., Steinberger, M., and McClure, J. E.. Equivariant stable homotopy theory, Lecture Notes in Math. 1213, Springer-Verlag, Berlin, 1986. With contributions by McClure, J. E..Google Scholar
13.McCarthy, Randy. Relative algebraic K-theory and topological cyclic homology. Acta Math. 179(2) (1997), 197–222.CrossRefGoogle Scholar
14.Soulé, Christophe. Rational K-theory of the dual numbers of aring of algebraic integers. In Algebraic K-theory (Evanston, Ill., 1980), Lecture Notes in Math. 854, pages 402–408. Springer-Verlag, New York, 1981.CrossRefGoogle Scholar
15.Staffeldt, R. E.. Rational algebraic K-theory of certain truncated polynomial rings. Proc. Amer. Math. Soc. 95 (1985), 191–198.Google Scholar
- 10
- Cited by

