Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kondo, Satoshi
and
Yasuda, Seidai
2018.
First and second K-groups of an elliptic curve over a global field of positive characteristic.
Annales de l'Institut Fourier,
Vol. 68,
Issue. 5,
p.
2005.

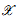 is an integral model of a smooth curve
is an integral model of a smooth curve 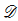 -elliptic sheaves of rank 2.
-elliptic sheaves of rank 2.