1. INTRODUCTION
Currently, the US Global Positioning System (GPS) and the Russian Global Navigation Satellite System (GLONASS) are the only two fully operational satellite positioning systems with global coverage. GPS uses Code Division Multiple Access (CDMA) techniques to differentiate the satellites. All the blocks of GPS satellites (i.e., Blocks IIA, IIR, IIR-M, and IIF) transmit at least two types of ranging codes: the Coarse/Acquisition (C/A) codes and the Precise (P) code. The C/A code is open to civilian users, and the P code is only available to military and authorised users through encryption into the Y-code. However, the P(Y) codes can still be tracked using special tracking techniques such as cross-correlation or Z-tracking (Ashjaee and Lorenz, Reference Ashjaee and Lorenz1992; Seeber, Reference Seeber2003. P.240–243). GLONASS mainly uses Frequency Division Multiple Access (FDMA) techniques to distinguish the satellites. Similar to GPS, GLONASS also has standard accuracy signals L1OF and L2OF open to the public and high accuracy signals L1SF and L2SF reserved for military (Russian Institute of Space Device Engineering, 2008).
With the modernisation of GNSS, multi-constellation and multi-frequency data processing are the foci of current GNSS research. GPS Block IIR-M satellites transmit the new L2C signal, which can enhance the use of L2 in high-precision applications. Moreover, a new civil signal L5 on a third carrier frequency band is being transmitted on the Block IIF satellites. The L5 signal is expected to improve the precision and robustness of the system, supporting ‘Safety of Life’ applications. Another new civil signal, L1C, will be available on the next-generation Block III satellites. GLONASS has started to use CDMA signals on the new GLONASS-K satellites to increase compatibility and interoperability with GPS and other GNSS systems. The European GNSS, Galileo, completed its experimental phase in 2008 and the In-Orbit Validation (IOV) phase in 2012. Galileo currently has four operational satellites in orbit and early services with reduced performance have been available since 2014. To date China has launched 17 satellites for the BeiDou Navigation Satellite System (BDS), which includes six Geosynchronous Earth Orbit (GEO) satellites, six Medium Earth Orbit (MEO) satellites, and five Inclined Geosynchronous Satellite Orbit (IGSO) satellites. BDS B1I and B2I signals are now available to the public, and the B2I signal will be gradually replaced by a better signal in the future (China Satellite Navigation Office, 2013). Japan launched one Quasi-Zenith Satellite System (QZSS) satellite ‘MICHIBIKI’ in 2010. It transmits almost the same signals as the GPS Block III satellites.
With the progress of GNSS modernisation, extensive research has been conducted to investigate the performance of multi-GNSS in terms of signal and measurement quality, positioning accuracy and precision, and positioning availability. After the launch of the first Block IIF satellite, Montenbruck et al. (Reference Montenbruck, Hugentobler, Dach, Steigenberger and Hauschild2012) reported its periodic inter-frequency clock variations, and proposed an empirical model to mitigate the variations with an accuracy of 1 cm. De Bakker et al. (Reference De Bakker, Tiberius, van der Marel and van Bree2012) analysed the Galileo E1B, and E5aQ signals; their results show the standard deviations of their DD CP measurements with zero and short baselines vary between 0·4 mm and 0·7 mm. While the authors also demonstrate mixed GPS-Galileo DD Ambiguity Resolution (AR), the positioning quality is not presented, possibly due to the insufficient number of Galileo satellites at that time. Later, Steigenberger et al. (Reference Steigenberger, Hugentobler and Montenbruck2013) showed Galileo positioning results with short baselines (19 m and 101 m). The results show the accuracy of CP positioning using four Galileo IOV satellites are from about 1 cm to 5 cm. In terms of BDS and QZSS, Montenbruck et al. (Reference Montenbruck, Hauschild, Steigenberger, Hugentobler, Teunissen and Nakamura2013) assessed the signal and measurement quality of regional BDS and QZSS satellites. The results show the IGSO CP noise and multipath errors are from 1 mm to 3 mm when the satellite is over about 45° elevation. Shi et al. (Reference Shi, Zhao, Hu and Liu2013) also report similar results in a short baseline (436 m) test, and the global BDS satellites are also not included in these assessments due to the insufficient BDS MEO satellites at that time. Combined GPS and BDS dual-frequency positioning results show that the combined system can improve the fixed solution precisions by more than 20% for GPS (Odolinski et al., Reference Odolinski, Odijk and Teunissen2014; Shi et al, Reference Shi, Zhao, Hu and Liu2013). Wang et al. (Reference Wang, Groves and Ziebart2012) use 3D city models to assess satellite visibility in an urban canyon environment. They predict that adding Galileo and BDS to GPS and GLONASS can improve the navigation reliability at most of the simulated city locations, and the availability (of more than four satellites) can reach 100% by 2020 at those locations. Lau et al. (Reference Lau, Tateshita and Sato2015) have carried out a case study on the impacts of multi-GNSS (GPS, GLONASS, and QZSS) on positioning accuracy and multipath errors in high-precision single-epoch solutions. The results show the impact of combining GNSS systems is not always beneficial compared with GPS-only solutions. Lau et al. (Reference Lau, Tateshita and Sato2015) show this is due to the introduction of more multipath errors in their selected difficult environments.
The number of visible satellites and new signals are increasing. They provide users with more observations, and hence increase redundancy in parameter estimation. When so many satellites and signals are available, surveyors and other high-precision GNSS users may not have a clear idea about what GNSS constellations or their combinations can be optimally used, what the corresponding achievable accuracy and precision would be, and if more systems/signals can always bring about improved results. Therefore, it is important to investigate the performance of multi-GNSS (GPS, GLONASS, Galileo, QZSS, and regional and global BDS) on a wider range of new signals (assessment on GPS L2C and L5 is not found in the literature) for positioning, especially in the signal domain.
This paper carries out an early assessment to perceive the impact of multi-GNSS (GPS, GLONASS, Galileo, BDS, and QZSS) on high-precision CP-based positioning with the following objectives:
• To study the effect of measurement noise levels in all currently available signals by investigating their DD CP residuals (Test 1).
• To evaluate positioning precision, accuracy, and fixed solution availability using the selected individual GNSS constellations and their selected combinations in good and realistic environments, i.e. low multipath (Test 2) and severe multipath environments (Test 3).
2. DESCRIPTION OF TESTS AND METHODOLOGIES
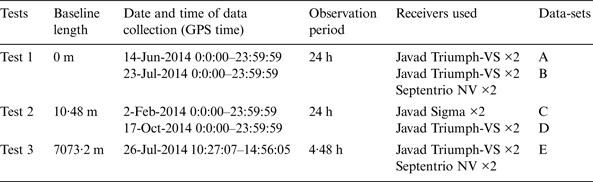
All the tests were carried out in Ningbo, China. Ningbo is located in a good GNSS area, where access to the signals from multiple constellations including GPS, GLONASS, Galileo, QZSS, and regional and global BDS is available. Three tests were carried out with zero, 10 m, and 7 km baselines as listed in Table 1. Tests 1 and 2 were conducted on known points for 24 hours, with two multi-GNSS receivers continuously operating and logging the raw observation data. All the receivers in Test 1 were connected to a Leica AR20 choke-ring antenna located on the North Pillar on the roof of the University of Nottingham Ningbo China (UNNC) Science and Engineering Building (SEB) via a GEMS GS18 signal splitter. In Test 2, two Javad receivers were connected to two Leica AR20 choke-ring antennas on the North Pillar and the South Pillar on the roof of the SEB building, respectively. Since the Javad Triumph receivers were not available on 2 February 2014 (this date is chosen because four Galileo satellites could be simultaneously observed), Javad Sigma receivers were used instead to collect data. The North Pillar was used as a reference station in Test 3, and the rover station was set on the roof of another building with a baseline length of about 7 km. The reason to choose this baseline length is that short baselines of several kilometre length are usually used in RTK surveying.
Table 1. List of relative positioning tests.

The CP residuals in Test 1 are obtained with the DD method. A single difference (SD) operation is performed for satellite p and receiver a and b by:
where ![]() $\varphi _{ab}^p $ is the SD CP, λ p is the signal wavelength of satellite p,
$\varphi _{ab}^p $ is the SD CP, λ p is the signal wavelength of satellite p, ![]() $\rho _{ab}^p $ is the SD range between satellite and receivers, c is the speed of light, dt ab is the SD receiver clock error,
$\rho _{ab}^p $ is the SD range between satellite and receivers, c is the speed of light, dt ab is the SD receiver clock error, ![]() $N_{ab}^p $ is the SD integer ambiguity, and
$N_{ab}^p $ is the SD integer ambiguity, and ![]() $\varepsilon _{ab}^p $ is the SD residual term. Then the DD operation is conducted for satellites p and q:
$\varepsilon _{ab}^p $ is the SD residual term. Then the DD operation is conducted for satellites p and q:
Since the baseline length is zero, all orbit errors, multipath effects, ionospheric and tropospheric biases can be eliminated, and ![]() $\displaystyle{1 \over {{\lambda _p}}}\rho _{ab}^p - \displaystyle{1 \over {{\lambda _q}}}\rho _{ab}^q $ is zero. The DD ambiguity,
$\displaystyle{1 \over {{\lambda _p}}}\rho _{ab}^p - \displaystyle{1 \over {{\lambda _q}}}\rho _{ab}^q $ is zero. The DD ambiguity, ![]() $N_{ab}^{pq} $, can be easily eliminated as well since it is an integer. The reference satellite p is defined by one satellite with the highest elevation angle at every epoch (the GPS satellites are chosen as the reference satellites when processing using the QZSS satellite because they have similar signal structure). For GPS and the other CDMA GNSS systems with the same wavelengths, the receiver clock error can be eliminated. The DD CP becomes:
$N_{ab}^{pq} $, can be easily eliminated as well since it is an integer. The reference satellite p is defined by one satellite with the highest elevation angle at every epoch (the GPS satellites are chosen as the reference satellites when processing using the QZSS satellite because they have similar signal structure). For GPS and the other CDMA GNSS systems with the same wavelengths, the receiver clock error can be eliminated. The DD CP becomes:
Therefore, the noise level of the CP measurement can be described by the DD CP residuals ![]() $\; \varepsilon _{ab}^{pq} $.
$\; \varepsilon _{ab}^{pq} $.
For GLONASS FDMA signals, the receiver clock error cannot be eliminated by the classical DD technique due to the different frequencies (and hence wavelengths) used for individual satellites. According to the method used by Wang (Reference Wang2000) and Ong et al. (Reference Ong, Petovello and Lachapelle2009), the strategy is to scale the SD CP into distances before DD operation:
where DD ambiguity ![]() $N_{ab}^{pq} $ and SD ambiguity
$N_{ab}^{pq} $ and SD ambiguity ![]() $N_{ab}^p $ are all integers, and
$N_{ab}^p $ are all integers, and ![]() $\bar \varepsilon _{ab}^{pq} = {\lambda _p}\varepsilon _{ab}^p - {\lambda _q}\varepsilon _{ab}^q $ (in metres). Two receivers a and b used in the tests are from the same manufacturer (either Javad or Septentrio).
$\bar \varepsilon _{ab}^{pq} = {\lambda _p}\varepsilon _{ab}^p - {\lambda _q}\varepsilon _{ab}^q $ (in metres). Two receivers a and b used in the tests are from the same manufacturer (either Javad or Septentrio).
All the data in Tests 2 and 3 are post-processed using RTKLIB (version 2.4.2) in kinematic single-epoch mode. All available signals assessed in Test 1 are used for data processing in Tests 2 and 3, 100% fixed positioning solutions are used to calculate the precision and accuracy. RTKLIB is open source software for GNSS data processing and analysis. Its functionalities include a precise positioning algorithm using GPS, GLONASS, Galileo, BDS, QZSS, and Satellite-Based Augmentation Systems (SBAS) (Takasu, Reference Takasu2013). In data processing, RTKLIB scales CP observations into distance, so that GLONASS receiver clock errors can be estimated. This is a common method for GLONASS AR. Another method is to estimate receiver clock errors from SD code pseudoranges (Takac, Reference Takac2009). Before DD is formed, RTKLIB selects a reference satellite with the highest elevation angle at each epoch, and no DD operation is performed between different systems except between GPS and QZSS. The data is processed with a combination of forward and reverse solutions (Kalman filter smoothing), with the elevation mask set at 15°. The ambiguity is resolved by LAMBDA (Least Squares Ambiguity Decorrelation Adjustment) and its extended MLAMBDA (Modified LAMBDA) method (Takasu, Reference Takasu2013; Teunissen, Reference Teunissen1993, Reference Teunissen1995). As the rover is stationary, the correctness of AR is validated by the final positioning solution. If the 3D residual error of a DD measurement of an epoch is greater than half of the observing wavelength, then it is considered as the wrong AR. The use of reverse solutions can increase the number of epochs with correct AR, so that more samples for signal quality assessment are available. Since the position of the rover station in Test 3 is unknown, its position was determined by static survey and post processing.
3. RESULTS
3.1. Zero-baseline test (Test 1) results
The DD CP residuals of some selected satellites of multi-GNSS (GPS, GLONASS, Galileo, BDS, and QZSS) for all available real signals from data collected are shown in Figures 1 to 4. The criterion of selection is to choose satellites with as many observations as possible. In Figure 1, the top five plots show the DD CP residuals of satellite PRN30 with all GPS signals and their frequency histograms. The last plot shows the elevation angles of satellite PRN30 and its reference satellites (there are some overlapping lines but easy to recognise). In Figures 1 and 5 there are more than one reference satellite during some epochs. This is because for L2C and L5 signals transmitted by GPS satellite Blocks IIR-M (L2C), IIF (L2C and L5), and the QZSS satellite, the reference satellites are selected from the same blocks to compute residuals. Though the new L2C and L5 signals are currently available, they are still in a pre-operational state (National Coordination Office for Space-Based Positioning, Navigation, and Timing, 2014), and signal interruption occurred during the tests (for example in Figure 1, there is no L2C from satellite PRN30 after epoch about 288,000).

Figure 1. GPS DD CP residual for PRN30 in Test 1.

Figure 2. GLONASS DD CP residual for PRN01 in Test 1.

Figure 3. Galileo DD CP residual for PRN19 in Test 1.

Figure 4. BDS DD CP residual for PRN09 in Test 1.

Figure 5. QZSS DD CP residual for satellite Michibiki in Test 1.
From Figures 1 to 5, it can be seen that all the DD CP residuals follow statistical normal distributions. Also, the standard deviations of the residuals increase with the decrease in satellite elevation angle, especially for GPS P(Y) signals. As stated in Section 2, the reference satellite in DD is the highest elevation satellite at each epoch, so there are no DDs for one satellite if the highest elevation satellite is itself. This situation can be seen in Figure 1 for L5 residual after about epoch 312,500, and the gaps in Figures 2, 4, and 5.
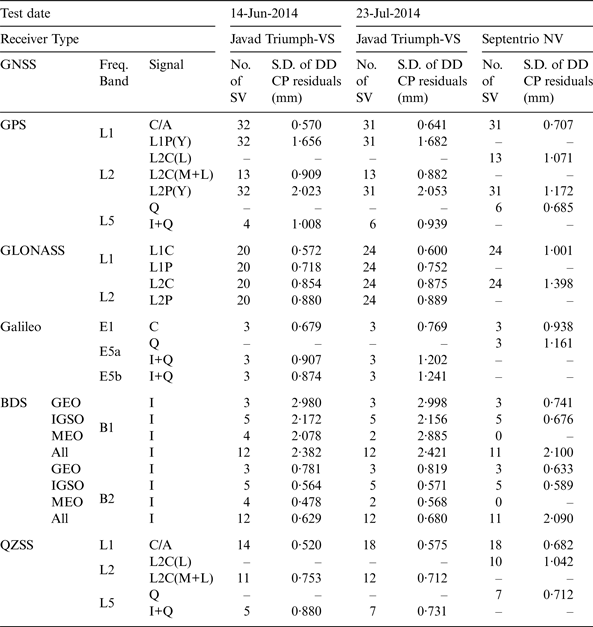
The standard deviations of residuals in all signals, modulations and the number of available satellites, are summarised in Table 2. Comparing the residuals in Column 5 (14 June 2014 / Javad Triumph-VS / S.D. of DD CP residuals) with the residuals in Column 7 (23 July 2014 / Javad Triumph-VS / S.D. of DD CP residuals), it can be seen for a receiver (Javad Triumph or Septentrio NV), the standard deviations of DD CP residuals between the two days (for each signal) are close, especially when there are enough satellites available for analysis. The Javad and Septentrio receivers generate CP measurements from different signal components when tracking some new signals (L2C and L5). The Septentrio NV receiver uses L2C(L) and L5(Q) while the Javad triumph receiver uses L2C(M + L) and L5(I + Q). Their tracking methods are not configurable by users, so it is not possible to compare the residuals of these new signals. The BDS residuals of the Septentrio datasets are always less than 1 mm if the signal transmitting satellites are from the same type of orbit such as GEO and IGSO, but the residuals are greater than 2 mm if two satellites in DD are from different types of orbits, while the residuals of Javad datasets are always above 2 mm for B1 and below 1 mm for B2. The results also show the noise of phase tracking of B1 signals in the Javad receiver is significantly higher than those of B2, while there is no big difference between B1 and B2 in the Septentrio receiver.
Table 2. Standard deviations (S.D.) of DD CP residuals using all available signals for all constellations in Test 1 (Elevation > 15°).

In summary, the DD CP residuals are between 0·5 mm and 1 mm for GPS and QZSS L1 C/A, L2C, and L5 signals, GLONASS L1 and L2 signals, and Galileo E1 signal. The DD CP residuals for GPS L1 P(Y) and L2 P(Y) signals, Galileo E5a and E5b are in the range between 1 mm and 2 mm. The BDS B1I residuals are over 2 mm when DD is formed with two satellites in two orbit types, and the B2I residuals are less than 1 mm when DD is formed with two satellites in the same orbit type.
3.2. Ten-metre baseline test (Test 2) results
3.2.1. Single constellation positioning results
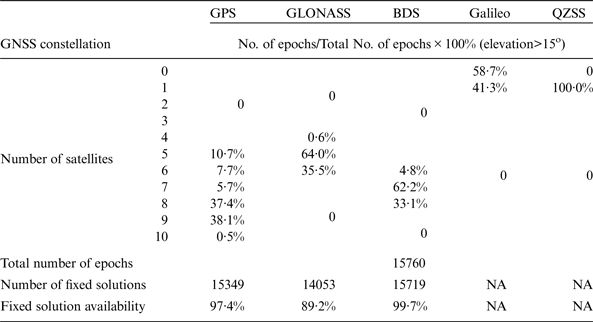
The fixed solution availability is the number of available epochs with fixed positioning solutions as a percentage of the total number of epochs. All the integer carrier phase ambiguities of observing satellites must be resolved correctly in fixed positioning solutions. The GNSS availabilities for Test 2 are summarised in Table 3. As shown in the table, GPS has very good fixed solution availabilities (over 99%) with at least four satellites available during the 24-hour observation period in Datasets C and D. GLONASS has a similarly high fixed solution availability of 98·58% in Dataset C but a low fixed solution availability of 84·31% in Dataset D with relatively fewer available satellites. The fixed solution availability for Galileo is currently low since there are currently only four satellites in orbit. No BDS result is presented in Dataset C because the receivers (Javad Sigma) used on that day cannot receive BDS signals, but a high fixed solution availability of 99·99% for BDS can be observed in Dataset D with at least six available satellites.
Table 3. The number of observed satellites and fixed solution availability of positioning with single constellations in Test 2.
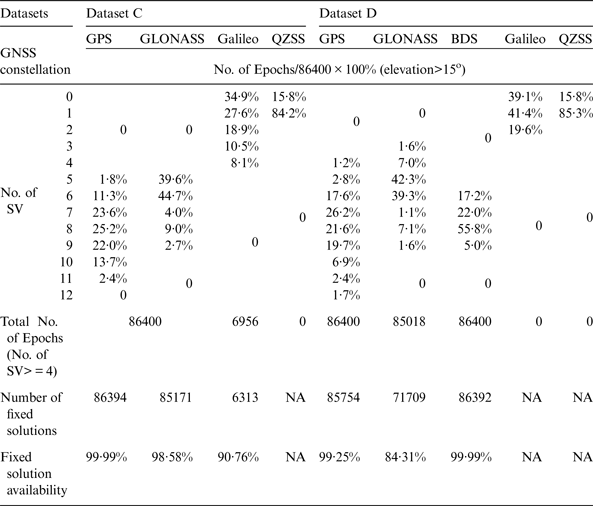
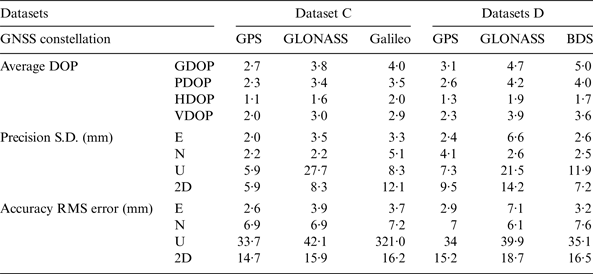
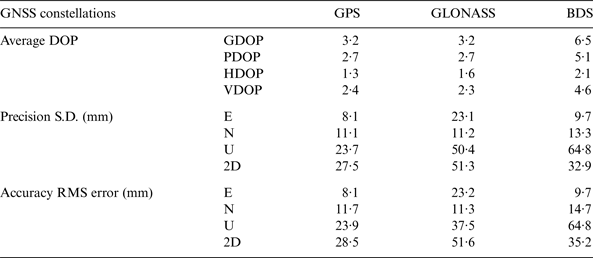
Table 4 shows the precision and accuracy results of Test 2 with average Dilution of Precision (DOP) values computed. The precision and accuracy are associated with the DOP values in the datasets. In Dataset C, GPS has the best precision at the millimetre level and the best accuracy at the centimetre level. Galileo, with a maximum of four satellites during the tests, can still achieve centimetre level accuracy and precision in plane coordinates, but it has the worst accuracy in height. For GLONASS, in spite of its low Horizontal DOP (HDOP), it has the worst precision in height. In Dataset D, the precisions and accuracies of GPS and GLONASS are relatively worse than those in Dataset C due to higher DOP value. Although BDS has higher DOPs than GPS, the precision and accuracy of BDS and GPS are close. This is because BDS has more observed satellites than GPS. Figure 6 shows the horizontal errors of the four GNSS systems in the two days. It shows GLONASS solutions have larger errors in Easting than Northing in the two days, but Galileo has larger error in Northing in the given dataset. GPS has an even spread of horizontal errors in Dataset C, but larger Northing errors in Dataset D.

Figure 6. Error distribution in the horizontal plane of GPS (a), GLONASS (b), Galileo (c) of Dataset C, and GPS (d), GLONASS (e), BDS (f) of Dataset D.
Table 4. Average DOPs, precision, accuracy of positioning with single constellations in Test 2.

The elongated scatters in Figures 6(d) and 6(e) are due to poor satellite geometry. To take the scatters in Figure 6(d) as an example, Figure 7 shows the DOPs for a 15° elevation mask, and solution errors in Easting, Northing, and height components in the time interval from 2:30 to 3:20. The number of tracked satellites decreased to five from about 3:00, the GDOP jumps from 3 to above 10. The geometry deteriorates until another satellite PRN10 rises at 3:10, and then the solution accuracy returns to a normal level.

Figure 7. Geometric DOP (GDOP), Position DOP (PDOP), Horizontal DOP (HDOP), and Vertical DOP (VDOP) (represented with yellow, pink, blue, and red lines, respectively) for a 15° elevation mask, and solution errors in Easting, Northing, and height components.
3.2.2. Multi-constellation positioning results
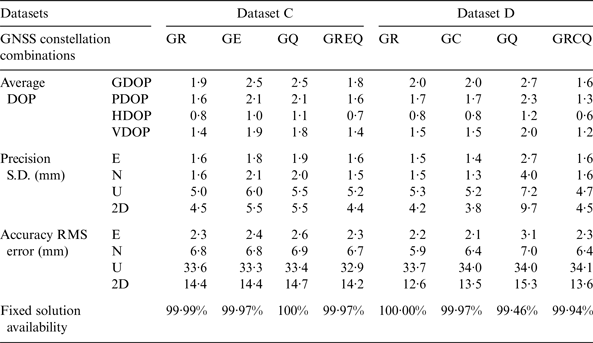
Average DOPs, precision, accuracy, and fixed solution availability of different combinations of GNSS constellations for Test 2 are summarised in Table 5. The combinations are GPS + GLONASS (GR), GPS + Galileo (GE), GPS + BDS (GC), GPS + QZSS (GQ), and all available constellations (GREQ or GRCQ). Compared with single constellation results in Table 4, there are slight improvements in both precision and accuracy in Dataset C when combining other constellations with GPS. The precision has been improved to about 5 mm in both horizontal and height components with two GNSS constellations, while accuracy improvement is insignificant. The best precision and accuracy are the combination of GREQ. The precision and accuracy results in Dataset D are close to those in Dataset C, except that GQ shows a slightly worse precision and accuracy than those of using GPS alone. This phenomenon has also been observed by Lau et al. (Reference Lau, Tateshita and Sato2015) as mentioned in Section 1, and it is also observed in the 7 km baseline test, which will be presented and analysed in Section 3.3.2.
Table 5. Average DOPs, precision, accuracy of positioning, and fixed solution availability of four combinations of constellations in Test 2.

In summary, Test 2 shows that if the baseline length is very short, millimetre level precision and centimetre level accuracy can usually be achieved with the fixed solution availability of over 90% in a good environment (CP residuals shown in Appendix A show it is a low multipath contaminated environment). The fixed solution availability can be improved to almost 100% when adding another constellation to GPS, but the precision and accuracy improvements are insignificant compared with using GPS alone. It can also be observed that using all constellations GREQ or GRCQ does not give 100% fixed solution availability, this phenomenon is more obvious in Test 3, and it will be discussed in Section 3.3.2.
3.3. 7 km baseline test (Test 3) results
3.3.1. Single constellation positioning results
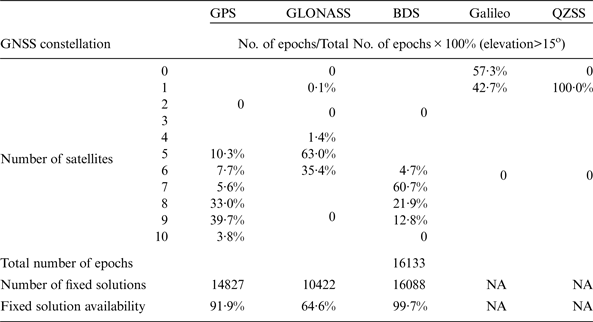
The GNSS availabilities in Test 3 using Javad and Septentrio receivers are summarised in Tables 6 and 7, respectively. Since there is only one Galileo satellite observed during the test, the Galileo data is excluded in the data processing because RTKLIB cannot perform a DD observation with mixed GNSS constellations. From the comparison of the Tests 2 and 3 with Javad datasets, the fixed solution availabilities of GPS and GLONASS show more than about 2% and 10% reductions, respectively (see the last row, Columns 2 and 3 of Tables 3 and 6). However, BDS has over 99% fixed solution availability in the test with at least six satellites. Comparing Table 6 with Table 7, it can be seen that the fixed solution availabilities for the Javad datasets are normally higher than those for the Septentrio datasets. Observations from the Septentrio dataset result in more failed AR than those from the Javad dataset when processed by RTKLIB, especially for GLONASS data. This is possibly due to a patented technique used by Javad receivers for GLONASS inter-channel bias calibration (Javad GNSS, 2013). One of the pieces of evidence is that the Signal to Noise Ratios (SNR) of Javad datasets are higher than those of Septentrio datasets (when the same antenna is used via a splitter).
Table 6. The number of satellites and fixed solution availability of single constellations with Javad Triumph-VS receivers in Test 3.

Table 7. The number of satellites and fixed solution availability of single constellations with Septentrio NV receivers in Test 3.

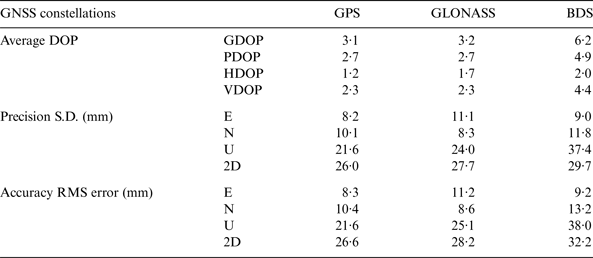
Tables 8 and 9 show the average DOPs, precision and accuracy results for Test 3 with Javad and Septentrio datasets. Opposite to the fixed solution availability, the Septentrio datasets have better precision and accuracy than the Javad datasets. This may indicate that the different signal tracking strategies of two models of receivers bring about different balances between accuracy and fixed solution availability. The precision and accuracy of the 7 km baseline test are at the centimetre level for all the GNSS constellations, and they are worse than the results in the 10 m baseline test due to increased baseline length. The two-dimensional error spread of GPS, GLONASS, and BDS solutions are plotted in Figure 8. GPS has better accuracy and precision than the other two systems as shown in Tables 8 and 9. Although BDS has more satellites than GLONASS (as presented in Tables 6 and 7), it has higher DOP values. The poor satellite geometry of BDS is due to the fact that there are only three MEO satellites observed in the test, and its GEO and IGSO satellites are at relatively high elevation angles. Besides, the circled solutions in Figure 8(b) are likely caused by multipath propagation. They are not excluded in Table 8 because these solutions are statistically in the same population. Nevertheless, the precision (U, 2D) and accuracy (U, 2D) would be (21·8 mm, 27·5 mm) and (22·6 mm, 28·7 mm), respectively, if the circled solutions in Figure 8(b) are excluded.

Figure 8. GPS (a,d), GLONASS (b,e), and BDS (c,f) positioning errors in horizontal plane with Javad Triumph (a,b,c) and Septentrio NV (d,e,f) receivers in Test 3.
Table 8. Average DOPs, precision, accuracy of single constellations with Javad Triumph-VS receiver in Test 3.

Table 9. Average DOPs, precision, and accuracy of single constellations with Septentrio NV receiver in Test 3.

3.3.2. Multi-constellation positioning results
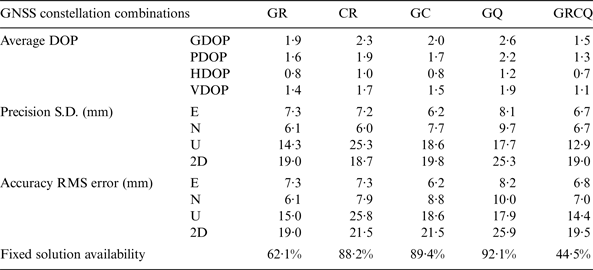
Average DOPs, precision, accuracy, and fixed solution availability of five selected combinations of GNSS constellations for Test 3 are summarised in Tables 10 and 11. The selected combinations are GR, CR, GC, GQ, and all available GNSS constellations (GRCQ). Compared with the fixed solution availabilities of single GNSS constellations in Tables 6 and 7, the fixed solution availability for combined two or more GNSS is lower than those of individual GNSS constellations (except GQ). The fixed solutions availability dramatically falls when using GRCQ. This is probably because the processing software RTKLIB cannot perform a DD between two different systems (except GQ), and the increased GNSS constellations and satellites increase the chance of multipath errors and leads to failed AR at some epochs. Multipath is the major GNSS error in practical RTK positioning. Pseudorange multipath errors in L1 (MP1) and L2 (MP2) are estimated with linear combinations of the pseudorange and carrier phase observations (Estey and Meertens, Reference Estey and Meertens1999), examples of MP1 and MP2 plots in Appendix B (Figures B1 and B2) show that the rover site in the 7 km baseline test has significant multipath effect on GNSS signals. Clear sinusoidal patterns of multipath signature can be found in ‘True’ error/residuals of some satellites with low elevation angles, examples are as shown in Appendix B (Figures B3 and B4).
Table 10. Average DOPs, precision, accuracy, and fixed solution availability of five combinations of constellations with Javad Triumph-VS receivers in Test 3.
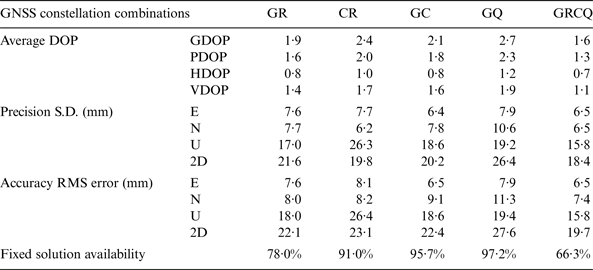
Table 11. Average DOPs, precision, accuracy, and fixed solution availability of five combinations of constellations with Septentrio NV receivers in Test 3.

In spite of decreased fixed solution availabilities of combining two or more GNSS constellations, Tables 10 and 11 show dual-constellations GR, CR and GC lead to obvious improvements in both accuracy and precision to about 2 cm. Comparing the single GNSS results in Tables 8 and 9, combination GQ (the second last column) increases the accuracy and precision by about 3% in the horizontal component and 18% in the height for both Javad and Septentrio receivers. For other combinations GR, CR and GC, the accuracy and precision in horizontal and height components are generally improved when comparing with single GPS, GLONASS, and BDS constellations by over 20%, 30% and 30%, respectively. However, there is an exception that combination CR in Septentrio dataset (the fourth column in Table 11) slightly deteriorates precision and accuracy in the height component compared to those of using GLONASS alone (the fourth column in Table 9). This is possibly caused by wrong AR due to the increased chance of multipath errors. It shows the impacts of combined GNSS systems compared with single GNSS solutions are not always beneficial.
4. CONCLUSIONS
This work has evaluated all the currently available GPS, GLONASS, Galileo, BDS and QZSS signals in a zero-baseline test, a 10 m-baseline test, and a 7 km baseline test. The carrier phase residuals in the zero-baseline test are obtained by the double difference (DD) method. In the 10 m and 7 km baseline tests the data are processed by the open source software RTKLIB with a combination of forward and reverse solutions and elevation mask of 15°.
In the zero-baseline test the data is collected on two different days by two sets of Javad and Septentrio receivers. The DD carrier phase residuals of all existing signals have been assessed. Statistical results show the residuals vary with different signals and models of receivers, but they are similar from day to day. Also, the standard deviation of the residuals is reduced with an increase in the satellite elevation angle and vice versa, especially for GPS P(Y) signals. The DD carrier phase residuals for GPS and QZSS L1 C/A, L2, and L5 signals, GLONASS L1 and L2 signals, and Galileo E1 signal are between 0·5 mm and 1 mm. The residuals for GPS L1P(Y) and L2P(Y) signals, Galileo E5a and E5b, are in the range between 1 mm and 2 mm. The BDS B1I residuals are over 2 mm when DD is performed with two satellites in two orbit types, and the B2I residuals are less than 1 mm when DD is performed with two satellites in the same orbit type.
The 10 m baseline test shows that in ideal conditions (i.e., a low multipath contaminated environment), using a single GNSS constellation (GPS, GLONASS, Galileo, or BDS) or their combinations can usually achieve millimetre-level precision and centimetre-level accuracy. The fixed solutions' availabilities are almost 100% except for Galileo, which is not at its Full Operational Capability. In the 7 km baseline test, both the positioning precision and accuracy reduce to the centimetre level. These results may provide surveyors with an idea of the achievable performance of the GNSS combinations in RTK surveying. A trade-off between fixed solution availability and accuracy has been observed in the datasets: using dual-constellations, such as GPS + GLONASS, GPS + BDS, GLONASS + BDS, and all available constellations (GPS + GLONASS + BDS + QZSS) can usually improve the precision and accuracy to about 2 cm in both plane and height components. However, using all available GNSS constellations can dramatically decrease the fixed solution availability, and using dual-constellations (e.g. GPS + QZSS in the 10 m baseline test and GLONASS + BDS in the 7 km baseline test) may slightly deteriorate precision and accuracy in some datasets. The reason is likely to be increased GNSS constellations and satellite numbers can introduce more multipath errors and lead to failed or wrong AR at some epochs.
Based on the results of this research, there are two directions of future work. Firstly, the results from the zero-baseline test are helpful in developing a stochastic model for multi-GNSS data processing. Proper weight can be assigned for carrier phase measurements according to the corresponding signal quality and satellite elevation angle. The second direction, from the observed trade-off between fixed solution availability and accuracy in Test 3, is to develop a better algorithm for satellite and signal selection to improve accuracy without compromising fix solution availability when using two or more GNSS constellations.
ACKNOWLEDGEMENTS
This work was carried out at the International Doctoral Innovation Centre (IDIC). The authors acknowledge the financial support from Ningbo Education Bureau, Ningbo Science and Technology Bureau, China's MOST and The University of Nottingham. The work is also partially supported by EPSRC grant No EP/L015463/1.
APPENDIX A. FIGURE FOR GPS CP RESIDUALS IN TEST 2

Figure A1. GPS L1 C/A DD carrier phase residuals (17-Oct-2014 dataset).
APPENDIX B. FIGURE FOR MULTIPATH COMBINATIONS AND CP RESIDUALS IN TEST 3

Figure B1. GPS L1 (left) and L2 (right) SNR and multipath combination of PRN15 in the 7 km baseline dataset.

Figure B2. GLONASS L1 (left) and L2 (right) SNR and multipath combination of SV03 in the 7 km baseline dataset.

Figure B3. ‘True’ error/residuals in L1 C/A and L2P CP of GPS PRN15 in the 7 km baseline dataset.

Figure B4. ‘True’ error/residuals in L1C and L2C of GLONASS SV17 in the 7 km baseline dataset.