Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Belanger, David R.
2015.
Weak Truth Table Degrees of Structures.
Notre Dame Journal of Formal Logic,
Vol. 56,
Issue. 2,
DOWNEY, ROD
and
GREENBERG, NOAM
2018.
A HIERARCHY OF COMPUTABLY ENUMERABLE DEGREES.
The Bulletin of Symbolic Logic,
Vol. 24,
Issue. 1,
p.
53.

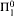 subsets of 2
subsets of 2