Article contents
Π11 relations and paths through 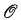
Published online by Cambridge University Press: 12 March 2014
Extract
When bounds on complexity of some aspect of a structure are preserved under isomorphism, we refer to them as intrinsic. Here, building on work of Soskov [34], [33], we give syntactical conditions necessary and sufficient for a relation to be intrinsically 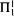 on a structure. We consider some examples of computable structures
on a structure. We consider some examples of computable structures 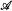 and intrinsically
and intrinsically 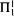 relations R. We also consider a general family of examples of intrinsically
relations R. We also consider a general family of examples of intrinsically 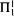 relations arising in computable structures of maximum Scott rank.
relations arising in computable structures of maximum Scott rank.
For three of the examples, the maximal well-ordered initial segment in a Harrison ordering, the superatomic part of a Harrison Boolean algebra, and the height-possessing part of a Harrison p-group, we show that the Turing degrees of images of the relation in computable copies of the structure are the same as the Turing degrees of 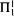 paths through Kleene's
paths through Kleene's 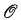 . With this as motivation, we investigate the possible degrees of these paths. We show that there is a
. With this as motivation, we investigate the possible degrees of these paths. We show that there is a 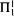 path in which ∅′ is not computable. In fact, there is one in which no noncomputable hyperarithmetical set is computable. There are paths that are Turing incomparable, or Turing incomparable over a given hyperarithmetical set. There is a pair of paths whose degrees form a minimal pair. However, there is no path of minimal degree.
path in which ∅′ is not computable. In fact, there is one in which no noncomputable hyperarithmetical set is computable. There are paths that are Turing incomparable, or Turing incomparable over a given hyperarithmetical set. There is a pair of paths whose degrees form a minimal pair. However, there is no path of minimal degree.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2004
References
REFERENCES
- 14
- Cited by

