Hostname: page-component-7dd5485656-c8zdz Total loading time: 0 Render date: 2025-10-27T09:36:08.228Z Has data issue: false hasContentIssue false
  • English
  • Français

AN ORDER ANALYSIS OF HYPERFINITE BOREL EQUIVALENCE RELATIONS

Part of: Computability and recursion theory Set theory Connections with other structures, applications

Published online by Cambridge University Press:  21 March 2025

SU GAO Open the ORCID record for SU GAO [Opens in a new window]  and
MING XIAO Open the ORCID record for MING XIAO [Opens in a new window]
SU GAO
Affiliation:
SCHOOL OF MATHEMATICAL SCIENCES AND LPMC NANKAI UNIVERSITY TIANJIN 300071 P.R. CHINA E-mail: sgao@nankai.edu.cn
MING XIAO*
Affiliation:
SCHOOL OF MATHEMATICAL SCIENCES AND LPMC NANKAI UNIVERSITY TIANJIN 300071 P.R. CHINA
*
E-mail: ming.xiao@nankai.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we first consider hyperfinite Borel equivalence relations with a pair of Borel 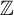$\mathbb {Z}$-orderings. We define a notion of compatibility between such pairs, and prove a dichotomy theorem which characterizes exactly when a pair of Borel 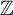$\mathbb {Z}$-orderings are compatible with each other. We show that, if a pair of Borel 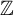$\mathbb {Z}$-orderings are incompatible, then a canonical incompatible pair of Borel 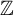$\mathbb {Z}$-orderings of 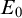$E_0$ can be Borel embedded into the given pair. We then consider hyperfinite-over-finite equivalence relations, which are countable Borel equivalence relations admitting Borel 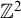$\mathbb {Z}^2$-orderings. We show that if a hyperfinite-over-hyperfinite equivalence relation E admits a Borel 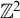$\mathbb {Z}^2$-ordering which is self-compatible, then E is hyperfinite.

Keywords

Borel equivalence relationsBorel partial ordersorder analysis

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 54H05: Descriptive set theory (topological aspects of Borel, analytic, projective, etc. sets) 03D65: Higher-type and set recursion theory

Information

Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 23
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Boykin, C. M. and Jackson, S., Borel boundedness and the lattice rounding property , Advances in Logic , vol. 425, Contemporary Mathematics, American Mathematical Society, Providence, 2007, pp. 113–126.CrossRefGoogle Scholar
Chen, R. and Kechris, A.S., Structurable equivalence relations . Fundamenta Mathematicae , vol. 242 (2018), no. 2, pp. 109–185.CrossRefGoogle Scholar
Connes, A., Feldman, J., and Weiss, B., An amenable equivalence relation is generated by a single transformation . Ergodic Theory and Dynamical Systems , vol. 1 (1981), pp. 431–450.CrossRefGoogle Scholar
Dougherty, R., Jackson, S., and Kechris, A.S., The structure of hyperfinite Borel equivalence relations . Transactions of the American Mathematical Society , vol. 341 (1994), no. 1, pp. 193–225.Google Scholar
Effros, E., Transformation groups and ${C}^{\ast }\kern-1.2pt$ -algebras . Annals of Mathematics (2) , vol. 81 (1965), pp. 38–55.CrossRefGoogle Scholar
Feldman, J. and Moore, C.C., Ergodic equivalence relations, cohomology and von Neumann algebras. I . Transactions of the American Mathematical Society , vol. 234 (1977), pp. 289–324.CrossRefGoogle Scholar
Frisch, J., Shinko, F., and Vidnyanszky, Z., Hyper-hyperfiniteness and complexity, preprint, 2024, arXiv:2409.16445.Google Scholar
Gao, S., Invariant Descriptive Set Theory , CRC Press, Boca Raton, 2009.Google Scholar
Harrington, L., Kechris, A. S., and Louveau, A., A Glimm-Effros dichotomy for Borel equivalence relations . Journal of American Mathematical Society , vol. 3 (1990), no. 4, pp. 903–928.CrossRefGoogle Scholar
Harrington, L., Marker, D., and Shelah, S., Borel orderings . Transactions of the American Mathematical Society , vol. 310 (1988), no. 1, pp. 293–302.Google Scholar
Hjorth, G. and Kechris, A. S., New dichotomies for Borel equivalence relations . Bulletin of Symbolic Logic , vol. 3 (1997), no. 3, pp. 329–346.CrossRefGoogle Scholar
Jackson, S., Kechris, A. S., and Louveau, A., Countable Borel equivalence relations . Journal of Mathematical Logic , vol. 2 (2002), no. 1, pp. 1–80.CrossRefGoogle Scholar
Kanovei, V., When a partial Borel order is linearizable . Fundamenta Mathematicae , vol. 155 (1998), no. 3, pp. 301–309.CrossRefGoogle Scholar
Kechris, A.S., Amenable equivalence relations and Turing degrees . Journal of Symbolic Logic , vol. 56 (1991), no. 1, pp. 182–194.CrossRefGoogle Scholar
Kechris, A.S., Classical Descriptive Set Theory , Springer–Verlag, New York, 1995.CrossRefGoogle Scholar
Kechris, A.S. and Louveau, A., The classification of hypersmooth equivalence relations . Journal of the American Mathematical Society , vol. 10 (1997), no. 1, pp. 215–242.CrossRefGoogle Scholar
Moschovakis, Y., Descriptive Set Theory , Second ed., American Mathematical Society, Providence, 2009.CrossRefGoogle Scholar
Thornton, R., ${\Delta}_1^1$ effectivization in Borel combinatorics, The Journal of Symbolic Logic, Published online (2024), 1–24. doi:10.1017/jsl.2024.38CrossRefGoogle Scholar
Slaman, T. and Steel, J., Definable functions on degrees , Cabal Seminar 81-85, 37–55 , vol. 1333, Lecture Notes in Mathematics, Springer-Verlag, Berlin, Heidelberg, 1988.Google Scholar
Weiss, B., Measure dynamics , Conference in Modern Analysis and Probability (New Haven, Conn., 1982), vol. 26, Contemporary Mathematics, American Mathematical Society, Providence, RI, 1984, pp. 395–421.CrossRefGoogle Scholar