The results that follow are intended to be understood as informal counterparts to formal theorems of Zermelo-Fraenkel set theory with choice. Basic notation not explained here can usually be found in [5]. It will also be necessary to assume a knowledge of the fundamentals of boolean and generic extensions, in the style of Jech's monograph [3]. Consistency results will be stated as assertions about the existence of certain complete boolean algebras, B, C, etc., either outright or in the sense of a countable standard transitive model M of ZFC augmented by hypotheses about the existence of various large cardinals. Proofs will usually be phrased in terms of the forcing relation ⊩ over such an M, especially when they make heavy use of genericity. They are then assertions about Shoenfield-style P-generic extensions M(G), in which the ‘names’ are required without loss of generality to be elements of MB = (VB)M, B is the boolean completion of P in M (cf. [3, p. 50]: the notation there is RO(P)), the generic G is named by Ĝ ∈ MB such that (⟦p ∈ Ĝ⟧B = p and 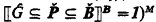(cf. [11, p. 361] and [3, pp. 58–59]), and for p ∈ P and c1, …, cn ∈ MB, p ⊩ φ(c1, …, cn) iff ⟦φ(c1, …, cn)⟧B ≥ p (cf. [3, pp. 61–62]).

Some prior acquaintance with large cardinal theory is also needed. At this writing no comprehensive introductory survey is yet in print, though [1], [10], [12]and [13] provide partial coverage. The scheme of definitions which follows is intended to fix notation and serve as a glossary for reference, and it is followed in turn by a description of the results of the paper. We adopt the convention that κ, λ, μ, ν, ρ and σ vary over infinite cardinals, and all other lower case Greek letters (except χ, φ, ψ, ϵ) over arbitrary ordinals.