Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-29T04:34:21.842Z Has data issue: false hasContentIssue false
  • English
  • Français

BOREL FUNCTORS AND INFINITARY INTERPRETATIONS

Published online by Cambridge University Press:  05 October 2018

MATTHEW HARRISON-TRAINOR ,
RUSSELL MILLER  and
ANTONIO MONTALBÁN
MATTHEW HARRISON-TRAINOR
Affiliation:
GROUP IN LOGIC AND THE METHODOLOGY OF SCIENCE UNIVERSITY OF CALIFORNIA BERKELEY, CA, USA
RUSSELL MILLER
Affiliation:
MATHEMATICS DEPT., QUEENS COLLEGE PH.D. PROGRAMS IN MATHEMATICS & COMPUTER SCIENCE GRADUATE CENTER, CITY UNIVERSITY OF NEW YORK NEW YORK, NY, USAE-mail:russell.miller@qc.cuny.eduURL: http://qcpages.qc.cuny.edu/∼rmiller
ANTONIO MONTALBÁN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA BERKELEY, CA, USAE-mail:antonio@math.berkeley.eduURL: www.math.berkeley.edu/∼antonio
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce the notion of infinitary interpretation of structures. In general, an interpretation between structures induces a continuous homomorphism between their automorphism groups, and furthermore, it induces a functor between the categories of copies of each structure. We show that for the case of infinitary interpretation the reversals are also true: every Baire-measurable homomorphism between the automorphism groups of two countable structures is induced by an infinitary interpretation, and every Baire-measurable functor between the set of copies of two countable structures is induced by an infinitary interpretation. Furthermore, we show that the complexities are maintained in the sense that if the functor is 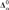${\bf{\Delta }}_\alpha ^0$, then the interpretation that induces it is 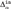${\rm{\Delta }}_\alpha ^{in}$ up to 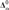${\bf{\Delta }}_\alpha ^0$ equivalence.

Keywords

03D4503C75interpretationsBorel functorsautomorphism groups
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 4 , December 2018 , pp. 1434 - 1456
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

*

Current address: DEPARTMENT OF PURE MATHEMATICS UNIVERSITY OF WATERLOO CANADA E-mail: maharris@math.uwaterloo.caURL: http://www.math.uwaterloo.ca/∼maharris/

References

REFERENCES

Ash, C. J. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North-Holland, Amsterdam, 2000.Google Scholar
Ahlbrandt, G. and Ziegler, M., Quasi-finitely axiomatizable totally categorical theories. Annals of Pure and Applied Logic, vol. 30 (1986), no. 1, pp. 63–82. Stability in model theory (Trento, 1984).CrossRefGoogle Scholar
Baldwin, J. T., Friedman, S. D., Koerwien, M., and Laskowski, M. C., Three red herrings around Vaught’s conjecture. Transactions of the American Mathematical Society, vol. 368 (2016), no. 5, pp. 3673–3694.CrossRefGoogle Scholar
Evans, D. M. and Hewitt, P. R., Counterexamples to a conjecture on relative categoricity. Annals of Pure and Applied Logic, vol. 46 (1990), no. 2, pp. 201–209.CrossRefGoogle Scholar
Gao, S., Invariant Descriptive Set Theory, Pure and Applied Mathematics, vol. 293, CRC Press, Boca Raton, FL, 2009.Google Scholar
Hjorth, G., A note on counterexamples to the Vaught conjecture. Notre Dame Journal of Formal Logic, vol. 48 (2007), no. 1, pp. 49–51.CrossRefGoogle Scholar
Hirschfeldt, D. R., Khoussainov, B., Shore, R. A., and Slinko, A. M., Degree spectra and computable dimensions in algebraic structures. Annals of Pure and Applied Logic, vol. 115 (2002), no. 1–3, pp. 71–113.CrossRefGoogle Scholar
Hodges, W., Model Theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, 1993.CrossRefGoogle Scholar
Harrison-Trainor, M., Igusa, G., and Knight, J. F., Some new computable structures of high rank. Preprint, 2016. Available at https://math.berkeley.edu/∼mattht/papers/high-scott-rank.pdf.Google Scholar
Harrison-Trainor, M., Melnikov, A., Miller, R., and Montalbán, A., Computable functors and effective interpretability, this Journal, vol. 82 (2017), no. 1, pp. 77–97.Google Scholar
Kueker, D. W., Definability, automorphisms, and infinitary languages, The Syntax and Semantics of Infinitary Languages (Barwise, J., editor), Springer, Berlin, Heidelberg, 1968, pp. 152–165.CrossRefGoogle Scholar
Makkai, M., An application of a method of Smullyan to logics on admissible sets. Bulletin de l’Académie polonaise des sciences. Série des sciences mathématiques, astronomiques, et physiques, vol. 17 (1969), pp. 341–346.Google Scholar
Montalbán, A., Computability theoretic classifications for classes of structures. Proceedings of ICM 2014, vol. 2 (2014), pp. 79-101.Google Scholar
Montalbán, A., A fixed point for the jump operator on structures, this Journal, vol. 78 (2013), no. 2, pp. 425–438.Google Scholar
Montalbán, A., A robuster Scott rank. Proceedings of the American Mathematical Society, vol. 143 (2015), no. 12, pp. 5427–5436.CrossRefGoogle Scholar
Miller, R., Poonen, B., Schoutens, H., and Shlapentokh, A., A computable functor from graphs to fields. Preprint, 2015. Available at https://arxiv.org/pdf/1510.07322.pdf.Google Scholar
Shelah, S., Can you take Solovay’s inaccessible away? Israel Journal of Mathematics, vol. 48 (1984), no. 1, pp. 1–47.CrossRefGoogle Scholar
Solovay, R. M., A model of set-theory in which every set of reals is Lebesgue measurable. Annals of Mathematics (2), vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar