Hostname: page-component-cb9f654ff-5jtmz Total loading time: 0 Render date: 2025-08-17T16:26:24.379Z Has data issue: false hasContentIssue false
  • English
  • Français

CODING IN GRAPHS AND LINEAR ORDERINGS

Part of: Computability and recursion theory Model theory

Published online by Cambridge University Press:  18 June 2020

JULIA F. KNIGHT ,
ALEXANDRA A. SOSKOVA  and
STEFAN V. VATEV
JULIA F. KNIGHT
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME NOTRE DAME, IN, USA E-mail: knight.1@nd.edu
ALEXANDRA A. SOSKOVA
Affiliation:
DEPARTMENT OF MATHEMATICAL LOGIC SOFIA UNIVERSITY SOFIA, BULGARIA E-mail: asoskova@fmi.uni-sofia.bg E-mail: stefanv@fmi.uni-sofia.bg
STEFAN V. VATEV
Affiliation:
DEPARTMENT OF MATHEMATICAL LOGIC SOFIA UNIVERSITY SOFIA, BULGARIA E-mail: asoskova@fmi.uni-sofia.bg E-mail: stefanv@fmi.uni-sofia.bg
Get access Rights & Permissions [Opens in a new window]

Abstract

There is a Turing computable embedding 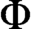$\Phi $ of directed graphs 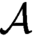$\mathcal {A}$ in undirected graphs (see [15]). Moreover, there is a fixed tuple of formulas that give a uniform effective interpretation; i.e., for all directed graphs 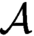$\mathcal {A}$, these formulas interpret 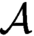$\mathcal {A}$ in 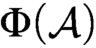$\Phi (\mathcal {A})$. It follows that 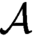$\mathcal {A}$ is Medvedev reducible to 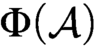$\Phi (\mathcal {A})$ uniformly; i.e., 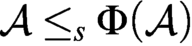$\mathcal {A}\leq _s\Phi (\mathcal {A})$ with a fixed Turing operator that serves for all 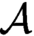$\mathcal {A}$. We observe that there is a graph G that is not Medvedev reducible to any linear ordering. Hence, G is not effectively interpreted in any linear ordering. Similarly, there is a graph that is not interpreted in any linear ordering using computable 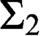$\Sigma _2$ formulas. Any graph can be interpreted in a linear ordering using computable 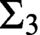$\Sigma _3$ formulas. Friedman and Stanley [4] gave a Turing computable embedding L of directed graphs in linear orderings. We show that there is no fixed tuple of 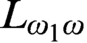$L_{\omega _1\omega }$-formulas that, for all G, interpret the input graph G in the output linear ordering 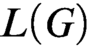$L(G)$. Harrison-Trainor and Montalbán [7] have also shown this, by a quite different proof.

Keywords

effective interpretabilityturing computable embedding

MSC classification

Primary: 03C57: Effective and recursion-theoretic model theory
Secondary: 03D45: Theory of numerations, effectively presented structures

Information

Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 2 , June 2020 , pp. 673 - 690
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Ash, C. J. and Knight, J. F., Computable Structures and the Hyperarithmetical Hierarchy, Elsevier, Amsterdam, 2000.Google Scholar
Baleva, V., The jump operation for structure degrees . Archive for Mathematical Logic, vol. 45 (2006), no. 3, pp. 249–265.CrossRefGoogle Scholar
Calvert, W., Cummins, D., Knight, J. F., and Miller, S., Comparing classes of finite structures . Algebra and Logic, vol. 43 (2004), no. 6, pp. 374–392.CrossRefGoogle Scholar
Friedman, H. and Stanley, L., A Borel reducibility theory for classes of countable structures , this Journal, vol. 54 (1989), no. 3, pp. 894–914.Google Scholar
Harrison-Trainor, M., Melnikov, A., Miller, R., and Montalbán, A., Computable functors and effective interpretability , this Journal, vol. 82 (2017), no. 1, pp. 77–97.Google Scholar
Harrison-Trainor, M., Miller, R., and Montalbán, A., Borel functors and infinitary interpretations , this Journal, vol. 83 (2018), no. 4, pp. 1434–1456.Google Scholar
Harrison-Trainor, M. and Montalbán, A., The tree of tuples of a structure, preprint.Google Scholar
Hirschfeldt, D., Khoussainov, B., Shore, R., and Slinko, A., Degree spectra and computable dimension in algebraic structures . Annals of Pure and Applied Logic, vol. 115 (2002), pp. 71–113.CrossRefGoogle Scholar
Kalimullin, I., Algorithmic reducibilities of algebraic structures . Journal of Logic and Computation, vol. 22 (2012), no. 4, pp. 831–843.CrossRefGoogle Scholar
Knight, J. F., Degrees coded in jumps of orderings , this Journal, vol. 51 (1986), no. 4, pp. 1034–1042.Google Scholar
Knight, J. F., Miller, S., and Vanden Boom, M., Turing computable embeddings , this Journal, vol. 72 (2007), no. 3, pp. 901–918.Google Scholar
Lavrov, I. S., Effective inseparability of the set of identically true formulae and finitely refutable formulae for certain elementary theories . Algebra and Logic, vol. 2 (1963), pp. 5–18.Google Scholar
Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas . Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.CrossRefGoogle Scholar
Mal’tsev, A., Some correspondences between rings and groups . Matematicheskii Sbornik. New Series, vol. 50 (1960), pp. 257–266.Google Scholar
Marker, D., Model Theory: An Introduction, GTM, Springer, New York, 2002.Google Scholar
Mekler, A., Stability of nilpotent groups of class 2 and prime exponent , this Journal, vol. 46 (1981), pp. 781–788.Google Scholar
Miller, R., Poonen, B., Schoutens, H., and Shlapentokh, A., A computable functor from graphs to fields , this Journal, vol. 83 (2018), no. 1, pp. 326–348.Google Scholar
Montalbán, A., Notes on the jump of a structure , Mathematical Theory and Computational Practice. Proceedings of CiE, 2009 (Ambos-Spies, K., Löwe, B., and Merkle, W., editors), Lecture Notes in Computer Science, vol. 5635, Springer, Berlin, Heidelberg, New York, 2009, pp. 372–378.Google Scholar
Montalbán, A., Computable Structure Theory . Perspectives in Logic, ASL and Cambridge University Press, to appear.Google Scholar
Nies, A., Undecidable fragments of elementary theories . Algebra Universalis, vol. 35 (1996), no. 1, pp. 8–33.CrossRefGoogle Scholar
Richter, L. J., Degrees of structures , this Journal, vol. 46 (1981), no. 4, pp. 723–731.Google Scholar
Soskova, A. A. and Soskov, I. N., A jump inversion theorem for the degree spectra . Journal of Logic and Computation, vol. 19 (2009), pp. 199–215.CrossRefGoogle Scholar
Stukachev, A., A jump inversion theorem for the semilattices of sigma-degrees . Siberian Advances in Mathematics, vol. 20 (2009), pp. 68–74, English translation.CrossRefGoogle Scholar