Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Caicedo, Andrés Eduardo
2006.
Set Theory.
p.
83.
Asperó, David
2006.
Coding by club-sequences.
Annals of Pure and Applied Logic,
Vol. 142,
Issue. 1-3,
p.
98.
Asperó, David
and
Friedman, Sy-David
2009.
Large cardinals and locally defined well-orders of the universe.
Annals of Pure and Applied Logic,
Vol. 157,
Issue. 1,
p.
1.
Pantsulaia, Gogi Rauli
2011.
On ordinary and standard products of infinite family of σ-finite measures and some of their applications.
Acta Mathematica Sinica, English Series,
Vol. 27,
Issue. 3,
p.
477.
Sargsyan, Grigor
2013.
Descriptive inner model theory.
The Bulletin of Symbolic Logic,
Vol. 19,
Issue. 1,
p.
1.
Asperó, David
Holy, Peter
and
Lücke, Philipp
2015.
Forcing lightface definable well-orders without the GCH.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 5,
p.
553.

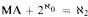
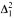 -
-