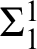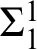Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MARCONE, ALBERTO
and
VALENTI, MANLIO
2021.
THE OPEN AND CLOPEN RAMSEY THEOREMS IN THE WEIHRAUCH LATTICE.
The Journal of Symbolic Logic,
Vol. 86,
Issue. 1,
p.
316.
Soldà, Giovanni
and
Valenti, Manlio
2023.
Algebraic properties of the first-order part of a problem.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 7,
p.
103270.
Kihara, Takayuki
2023.
Lawvere-Tierney topologies for computability theorists.
Transactions of the American Mathematical Society, Series B,
Vol. 10,
Issue. 2,
p.
48.
CIPRIANI, VITTORIO
MARCONE, ALBERTO
and
VALENTI, MANLIO
2025.
THE WEIHRAUCH LATTICE AT THE LEVEL OF
$\boldsymbol {\Pi }^1_1{-}\mathsf{CA}_0$
: THE CANTOR–BENDIXSON THEOREM.
The Journal of Symbolic Logic,
Vol. 90,
Issue. 2,
p.
752.