Hostname: page-component-7dd5485656-6kn8j Total loading time: 0 Render date: 2025-10-29T16:01:56.882Z Has data issue: false hasContentIssue false
  • English
  • Français

A completeness theorem for higher order logics

Published online by Cambridge University Press:  12 March 2014

Gábor Sági
Gábor Sági*
Affiliation:
Alfréd Rényi Mathematical Institute, Hungarian Academy of Sciences, Budapest PF. 127, H-1364 Hungary, E-mail: sagi@math-inst.hu
Get access Rights & Permissions [Opens in a new window]

Abstract

Here we investigate the classes 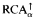of representable directed cylindric algebras of dimension α introduced by Németi [12]. 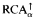can be seen in two different ways: first, as an algebraic counterpart of higher order logics and second, as a cylindric algebraic analogue of Quasi-Projective Relation Algebras. We will give a new, “purely cylindric algebraic” proof for the following theorems of Németi: (i) 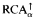is a finitely axiomatizable variety whenever α ≥ 3 is finite and (ii) one can obtain a strong representation theorem for 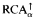if one chooses an appropriate (non-well-founded) set theory as foundation of mathematics. These results provide a purely cylindric algebraic solution for the Finitization Problem (in the sense of [11]) in some non-well-founded set theories.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 65 , Issue 2 , June 2000 , pp. 857 - 884
Copyright
Copyright © Association for Symbolic Logic 2000

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Aczel, P., Non-well-founded sets, CSLI Lecture Notes, no. 14, 1988.Google Scholar
[2]Andréka, H., Complexity of the equations valid in algebras of relations, Thesis for D.Sc (a post-habilitation degree) with Hungarian Academy of Sciences, Budapest, 1991.Google Scholar
[3]Andréka, H. and Németi, I., Connections between QRA's and CA's, Preprint, Miami, Florida International Univeristy, 1988.Google Scholar
[4]Baum, G.A., Haeberer, A.M., and Veloso, P.A.S., On the representability of the ∇-abstract relation algebra, IGPL Newsletter, vol. 1(3) (1992), pp. 3–4, European Foundation of Logic, Language and Information, Interest Group on Propositional and Predicate Logic.Google Scholar
[5]Henkin, L., Monk, D., and Tarski, A., Cylindric algebras, Part 1, North-Holland, Amsterdam, 1971.Google Scholar
[6]Henkin, L., Cylindric algebras, Part 2, North-Holland, Amsterdam, 1985.Google Scholar
[7]Kurucz, Á., Decision problems in algebraic logic, Ph.D. thesis, Budapest, 1997, Available on the following electronic address: http://circle.math-inst.hu/pub/algebraic-logic/.Google Scholar
[8]Kurucz, Á. and Németi, I., Representability of pairing relation algebras depends on your ontology, Preprint, Mathematical Institute of the Hungarian Academy of Sciences, Budapest, Available on the following electronic address: http://circle.math-inst.hu/pub/algebraic-logic/, 1997.Google Scholar
[9]Maddux, R., Some sufficient conditions for the representability of relation algebras, Algebra Universalis, vol. 8 (1978), pp. 162–172.CrossRefGoogle Scholar
[10]Mikulás, Sz., Sain, I., and Simon, A., Complexity of equational theory of relation algebras with projection elements, Bulletin of the Section of Logic, University of Lódz, vol. 21(3) (1992), pp. 103–111.Google Scholar
[11]Németi, I., Algebraization of quantifier logics, an introductory overview 12-th version, Mathematical Institute Budapest, Preprint, No. 13/1996, Available on the following electronic address: http://circle.math-inst.hu/pub/algebraic-logic/survey.dvi, An extended abstract of this appeared in Studia Logica vol. 50, No 3/4. pp. 485–569.Google Scholar
[12]Németi, I., Strong representability of fork algebras, a set theoretic foundation, Journal of IGPL, vol. 5 (1997), no. 1, pp. 3–23.CrossRefGoogle Scholar
[13]Németi, I. and Simon, A., Finitizable algebraic logic in some non-well-founded set theories, Preprint, Mathematical Institute of the Hungarian Academy of Sciences, 1995.Google Scholar
[14]Németi, I. and Simon, A., Weakly higher order cylindric algebras and finite axiomatization of the representables, Preprint, Mathematical Institute of the Hungarian Academy of Sciences, 1995.Google Scholar
[15]Sain, I. and Németi, I., Fork algebras in usual and in non-well-founded set theories (an overview), Logic at work (dedicated to the memory of Helena Rasiowa) (Orlowska, Ewa, editor), Physica-Verlag, Heidelberg, 1999, pp. 669–694.Google Scholar
[16]Sain, I. and Simon, A., The complexity of equational theory of relation algebras with projection elements, Preprint, Mathematical Institute of the Hungarian Academy of Sciences, Budapest, 1993.Google Scholar
[17]Tarski, A., Some metalogical results concerning the calculus of relations, this Journal, vol. 18 (1953), pp. 188–189.Google Scholar
[18]Tarski, A. and Givant, S., A formalization of set theory without variables, American Mathematical Society Colloquium Publications, vol. 41 (1988).Google Scholar
[19]Veloso, P.A.S. and Haeberer, A.M., A new algebra of first-order logic, Logic, methodology and philosophy of science, 9th international congress on logic, Uppsala, Sweden, 1991.Google Scholar