Article contents
The complexity of ODDnA
Published online by Cambridge University Press: 12 March 2014
Abstract
For a fixed set A. the number of queries to A needed in order to decide a set S is a measure of S's complexity. We consider the complexity of certain sets defined in terms of A:
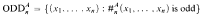
and, for m > 2,
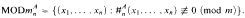
where #nA. (x1….. xn) = A(x1) + A(xn)(We identify 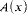 with
with 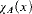 , where χA is the characteristic function of A.)
, where χA is the characteristic function of A.)
If A is a nonrecursive semirecursive set or if A is a jump, we give tight bounds on the number of queries needed in order to decide ODDnA and MODmnA:
• ODDnA can be decided with n parallel queries to A, but not with n − 1.
• ODDnA can be decided with ⌈log(n + 1)⌉ sequential queries to A but not with ⌈log(n + 1)⌉ − 1.
• MODmnA can be decided with ⌈n/m⌉ + ⌊n/m⌋ parallel queries to A but not with ⌈n/m⌉ + ⌊n/m⌋ − 1.
• MODmnA can be decided with ⌈log(⌈n/m⌉ + ⌊n/m⌋ + 1)⌉ sequential queries to A but not with ⌈log(⌈n/m⌉ + ⌊n/m⌋ + 1)⌉ − 1.
The lower bounds above hold for nonrecursive recursively enumerable sets A as well. (Interestingly, the lower bounds for recursively enumerable sets follow by a general result from the lower bounds for semirecursive sets.)
In particular, every nonzero truth-table degree contains a set A such that ODDnA cannot be decided with n − 1 parallel queries to A. Since every truth-table degree also contains a set B such that ODDnB can be decided with one query to B, a set's query complexity depends more on its structure than on its degree.
For a fixed set A,
Q(n, A) = {S: S can be decided with n sequential queries to A}.
Q∥ (n, A) = {S : S can be decided with n parallel queries to A}.
We show that if A is semirecursive or recursively enumerable, but is not recursive, then these classes form non-collapsing hierarchies:
• Q(0,A) ⊂ Q (1, A) ⊂ Q(2, A) ⊂ …
Q∥ (0, A) ⊂ Q∥ (1, A) ⊂ Q∥ (2, A) ⊂ …
The same is true if A is a jump.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000
References
REFERENCES
- 8
- Cited by

