Hostname: page-component-f554764f5-fr72s Total loading time: 0 Render date: 2025-04-18T20:55:51.626Z Has data issue: false hasContentIssue false
  • English
  • Français

Consequences of arithmetic for set theory

Published online by Cambridge University Press:  12 March 2014

Lorenz Halbeisen  and
Saharon Shelah
Lorenz Halbeisen
Affiliation:
Department of Mathematics, Eldgen. Technische Hochschule, Zürich, Switzerland, E-mail:halbeisen@math.ethz.ch
Saharon Shelah
Affiliation:
Institute of Mathematics, Hebrew University Jerusalem, Jerusalem., Israel, E-mail:shelah@math.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

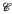In this paper, we consider certain cardinals in ZF (set theory without AC, the axiom of choice). In ZFC (set theory with AC), given any cardinals and 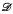, eithe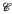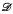r ≤ or 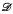≤ 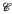. However, in ZF this is no longer so. For a given infinite set A consider seq1-1(A), the set of all sequences of A without repetition. We compare |seq1-1(A)|, the cardinality of this set, to |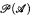|, the cardinality of the power set of A. What is provable about these two cardinals in ZF? The main result of this paper is that ZF ⊢ ∀A(| seq1-1(A)| ≠ |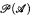|), and we show that this is the best possible result. Furthermore, it is provable in ZF that if B is an infinite set, then | fin(B)| < | 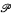(B*)| even though the existence for some infinite set B* of a function ƒ from fin(B*) onto 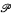(B*) is consistent with ZF.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 1 , March 1994 , pp. 30 - 40
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[Ba] Bachmann, H., Transfinite Zahlen, Springer-Verlag, Berlin, 1967.CrossRefGoogle Scholar
[Je1] Jech, Th., Set theory, Academic Press, New York, 1978.Google Scholar
[Je2] Jech, Th., The axiom of choice, North-Holland, Amsterdam, 1973.Google Scholar
[La] Läuchli, H., Auswahlaxiom in der Algebra, Commentarii Mathematici Hehetiei, vol. 37 (1962), pp. 1–18.Google Scholar
[Sl] Sloane, N. J. A., A handbook of integer sequence, Academic Press, New York, 1973.Google Scholar
[Sp1] Specker, E., Verallgemeinerte Kontinuumshypothese und Auswahlaxiom, Archiv der Mathematik, vol. 5 (1954), pp. 332–337.CrossRefGoogle Scholar
[Sp2] Specker, E., Zur Axiomatik der Mengenlehre, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 3 (1957), pp. 173–210.CrossRefGoogle Scholar