Article contents
Consistency and completeness of the theory of combinators
Published online by Cambridge University Press: 12 March 2014
Extract
The consistency of the theory of combinators, when based on the combinatory axioms, the rules of equality, and the equations

was proved in my thesis; likewise some theorems expressing certain completeness properties of this theory of combinatory equivalence formed the principal subject of that thesis and a succeeding paper. Further theorems of this sort were later demonstrated by Rosser; his theorems are, in some cases, more powerful than those just mentioned, but they apply to a weakened system. The purpose of this note is to discuss the extension of these theorems to the case where the whole of the theory of combinators is taken into account, and the rules for equality are derived from more fundamental considerations.
The paper is based on a formulation of the theory of combinators contained in a previous paper, acquaintance with which is presupposed.
A key theorem in investigations of this character is a theorem proved in 1936 by Church and Rosser. It is necessary to give a brief account of this theorem together with a generalization of it.
The theorem concerns a certain formalism, which I shall here call the λ-formalism. The terms of this formalism, which I shall call λ-terms, are constituted as follows. For primitive terms we have an infinite set of variables, together with certain constants, the nature of which is arbitrary. Further terms are formed by two operations: a binary operation (analogous to application in the theory of combinators) which combines two λ-terms 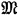 and
and 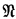 to form a new λ-term here symbolized by
to form a new λ-term here symbolized by 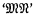 ; and another binary operation combining a variable x and a term
; and another binary operation combining a variable x and a term 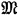 containing x as free variable to form a term
containing x as free variable to form a term 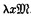 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1941
References
1 Grundlagen der kombinatorischen Logik, American journal of mathematics, vol. 52 (1930), pp. 509–536CrossRefGoogle Scholar, 789–834. This paper will be referred to hereafter as GKL, and the various subdivisions of the paper will be referred to according to the system used in the paper itself. The consistency was proved in II C 1 Satz 13, on p. 799.
2 Some additions to the theory of combinators, American journal of mathematics, vol. 54 (1932), pp. 551–558CrossRefGoogle Scholar. This paper will be referred to as ATC.
3 A mathematical logic without variables, Annals of mathematics, vol. 36 (1935), pp. 127–150CrossRefGoogle Scholar, and Duke mathematical journal, vol. 1 (1935), pp. 328–355CrossRefGoogle Scholar. References to Rosser refer, when no further explanation is given, to this paper. See also the paper by Church and Rosser cited below.
4 A revision of the fundamental rules of combinatory logic, this Journal, vol. 6 (1941), pp. 41–53Google Scholar. This paper will be cited as RFR.
5 Some properties of conversion, Transactions of the American Mathematical Society, vol. 39 (1936), pp. 472–482CrossRefGoogle Scholar.
6 For the applications it is convenient to suppose that there are primitive λ-terms which cannot function as variables—i.e., as the x in ![]() .
.
7 Church writes this ![]() . It is interpreted as meaning the value obtained by applying
. It is interpreted as meaning the value obtained by applying ![]() , considered as a function, to the argument
, considered as a function, to the argument ![]() . Church calls what is here designated ‘λ-term’ a ‘well-formed formula.’
. Church calls what is here designated ‘λ-term’ a ‘well-formed formula.’
8 This notion is here taken intuitively. For precise definitions of this and related notions in the λ-formalism see Kleene, S. C., Proof by cases informal logic, Annals of mathematics, vol. 35 (1933), see p. 530Google Scholar.
9 Since the λ is a prefixed binary operation, parentheses are unnecessary. Thus ![]() means automatically
means automatically ![]() , not
, not ![]() . However parentheses will sometimes be inserted in such cases for the sake of perspicuity, and of course they are necessary if the second of the above terms is meant rather than the first. If the other operation were indicated by a distinctive prefixed symbol, say ‘α’ or Chwistek's ‘*’, no parentheses at all would be necessary.
. However parentheses will sometimes be inserted in such cases for the sake of perspicuity, and of course they are necessary if the second of the above terms is meant rather than the first. If the other operation were indicated by a distinctive prefixed symbol, say ‘α’ or Chwistek's ‘*’, no parentheses at all would be necessary.
10 The motivation of these changes is that it may be easier to prove the consistency of stronger systems based on the theory of combinators if a normality condition such as is here expressed by ![]() is introduced. Such conditions were introduced by Rosser. If his R 2 is replaced by his M 13 his conditions are a special case of those here formulated. For the case where R 2 is used, we may note that the theorems below hold if we interpret the E in (i) and (ii) and Type I as Rosser's Σ; while in (iii) and Types II and III it is Rosser's E.
is introduced. Such conditions were introduced by Rosser. If his R 2 is replaced by his M 13 his conditions are a special case of those here formulated. For the case where R 2 is used, we may note that the theorems below hold if we interpret the E in (i) and (ii) and Type I as Rosser's Σ; while in (iii) and Types II and III it is Rosser's E.
11 In case the system is formulated with B, C, W, K as primitives instead of S and K, then the former are to be replaced respectively by B λ, C λ, W λ, K λ, where

12 The sign ‘=’ is to be regarded as defined by the equivalence ![]() . This is not to be confused with the equality of §5 below.
. This is not to be confused with the equality of §5 below.
13 E.g., if we require that x shall not appear more than once in ![]() (in order that
(in order that ![]() should be a λ-term), we have a form of conversion which goes with the system
should be a λ-term), we have a form of conversion which goes with the system ![]() with omission of the rules and axioms for W.
with omission of the rules and axioms for W.
14 There is only one term of this form.
15 Cf. Rosser's T 18.
16 A modification of the axiom Q0 is necessary in the case of GKL. Cf. Remark 1.
17 Note that ≌ here designates the primitive relation of the system ![]() ; whereas in §3 ‘=’ was a defined relation in regard to
; whereas in §3 ‘=’ was a defined relation in regard to ![]() . Of course
. Of course ![]() can be interpreted so that the two relations are the same; but this is a different interpretation from that used in Theorem 3.
can be interpreted so that the two relations are the same; but this is a different interpretation from that used in Theorem 3.
18 Apparent variables from the standpoint of combinatory logic, Annals of mathematics, vol. 34 (1934), pp. 381–104Google Scholar. The definition referred to is stated on page 390. Only obvious modifications are necessary to adapt it so as to be suitable for the system ![]() .
.
19 Instead of assigning a unique ![]() to every
to every ![]() , Rosser defines a one-many relation “
, Rosser defines a one-many relation “![]() denotes
denotes ![]() ”, and then proves (M 72) that if
”, and then proves (M 72) that if ![]() denotes
denotes ![]() and
and ![]() , then
, then ![]() . This procedure can, if desired, be followed here.
. This procedure can, if desired, be followed here.
20 For the reader who is familiar with GKL the argument of Rosser, up to M62, can be simplified as follows. In GKL, through II D, Ax. I2 has been used only in II B 2, II B 4 Satz 4, and in II D 1, 3 ff. to drop out factors of the form BmI. Without Ax. I2, however, we can replaced II B 4 Satz 4 by X×I = I×X. Then we can derive Rosser's M 53 directly; this requires first his F 12, F 16, then a proof by induction and II B 4 Satz 6 that
whence his M 53 follows as he indicates. (Here I write Bm instead of Bm because Rosser has shown it is the mth power of B). The proof of II D 2 Satz 1 then goes through with obvious modifications (cf. Rosser's F 26). Next by the method of The universal quantifier in combinatory logic §3 Theorem 8 (Annals of mathematics vol. 32 (1931), p. 165Google Scholar), we can show without using variables or the theorems of II E, that if X is a normal combinator (in the sense of GKL, or better ATC convention 3) of minimum order m and degree n, then
for p≦m and q≦n, and also
(or, if preferred
(The first of the properties to be established does not satisfy hypothesis (a) of Theorem 8 (I.c.); but if we use Theorem 7 and replace “order m and degree n” by “minimum order m and degree n,” then Theorem 8 can be established for normal combinators; cf. remark on p. 164, (I.c.).) From these properties it follows that where a factor of the form BmI occurs in a regular combinator, it can be absorbed in the factor to the left of it or passed across it, and this process can be continued until all these factors are at the beginning, where they may be combined by M 53. With this modification in II D 1 Satz 1 the transformation to a normal form of Rosser type goes through as in II D 3 ff.
- 4
- Cited by

