Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-559fc8cf4f-6pznq Total loading time: 0.26 Render date: 2021-03-07T10:20:16.273Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
The Journal of Symbolic Logic The Journal of Symbolic Logic

Article contents

The covering numbers of Mycielski ideals are all equal

Published online by Cambridge University Press:  12 March 2014

Saharon Shelah  and
Juris Steprāns
Saharon Shelah
Affiliation:
Institute of Mathematics, The Hebrew University, Jerusalem 91904, Israel, E-mail: shelah@math.huji.ac.il
Juris Steprāns
Affiliation:
Department of Mathematics, York University, 4700 Keele Street, Toronto Ontario, CanadaM3J 1P3, E-mail:steprans@mathstat.yorku.ca
Corresponding
E-mail address:
shelah@math.huji.ac.il
steprans@mathstat.yorku.ca
Get access
Rights & Permissions[Opens in a new window]

Abstract

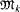The Mycielski ideal is defined to consist of all sets 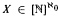A ⊆ ℕk such that {f ↾ X : f ∈ A} ≠ Xk for all . It will be shown that the covering numbers for these ideals are all equal. However, the covering numbers of the closely associated Rosłanowski ideals will be shown to be consistently different.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 2 , June 2001 , pp. 707 - 718
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below.
If you should have access and can't see this content please contact technical support.

References

[1]Balcerzak, Marek, Typical properties of continuous functions via the Vietoris topology. Real Analysis Exchange, vol. 18 (1992/1993), no. 2, pp. 532–536.Google Scholar
[2]Balcerzak, Marek and Rosłanowski, Andrzej, On Mycielski ideals, Proceedings ofthe American Mathematical Society, vol. 110 (1990), no. 1, pp. 243–250.CrossRefGoogle Scholar
[3]Cichoń, J., Rosłanowski, A., J. Steprāns, and Wȩglorz, B., Combinatorial properties of the ideal ƥ2, this Journal, vol. 58 (1993), no. 1, pp. 42–54.Google Scholar
[4]Hejduk, Jacek, Convergence with respect to the Mycielski σ-ideal, Demonstratio Mathematica, vol. 22 (1989), no. 1, pp. 43–50.CrossRefGoogle Scholar
[5]Kamo, Shizuo, Some remarks about Mycielski ideals, Colloquium Mathematicum, vol. 65 (1993), no. 2, pp. 291–299.CrossRefGoogle Scholar
[6]Mycielski, Jan, Some new ideals of sets on the real line, Colloquium Mathematicum, vol. 20 (1969), pp. 71–76.CrossRefGoogle Scholar
[7]Plewik, Szymon, On some problem of A. Roslanowski, Colloquium Mathematicum, vol. 69 (1995), no. 2, pp. 297–298.CrossRefGoogle Scholar
[8]Roslanowski, A., Mycielski ideals generated by uncountable systems, Colloquium Mathematicum, vol. 66 (1994), no. 2, pp. 187–200.CrossRefGoogle Scholar
[9]Rosłanowski, Andrzej, On game ideals, Colloquium Mathematicum, vol. 59 (1990), no. 2, pp. 159–168.CrossRefGoogle Scholar
[10]Schilling, Kenneth, A category base for Mycielski's ideals, Real Analysis Exchange, vol. 19 (1993/1994), no. 1, pp. 98–105.Google Scholar
[11]Sharp, James D. and Thomas, Simon, Uniformization problems and the cofinalily of the infinite symmetric group, Notre Dame Journal of Formal Logic, vol. 35 (1994), no. 3, pp. 328–345.Google Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 13 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 7th March 2021. This data will be updated every 24 hours.

2 Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

The covering numbers of Mycielski ideals are all equal
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

The covering numbers of Mycielski ideals are all equal
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

The covering numbers of Mycielski ideals are all equal
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *