Article contents
A decidable subclass of the minimal Gödel class with identity
Published online by Cambridge University Press: 12 March 2014
Extract
The minimal Gödel class with identity (MGCI) is the class of closed, prenex quantificational formulas whose prefixes have the form ∀x1∀x2∃x3 and whose matrices contain arbitrary predicate letters and the identity sign “=”, but contain no function signs or individual constants. The MGCI was shown undecidable (for satisfiability) in 1983 [Go2]; this both refutes a claim of Gödel's [Gö, p. 443] and settles the decision problem for all prefix-classes of quantification theory with identity.
In this paper, we show the decidability of a natural subclass of the MGCI. The formulas in this subclass can be thought of as exploiting only half of the power of the existential quantifier. That is, since an MGCI formula has prefix ∀x1∀x2∃x3, in general its truth in a model requires for any elements a and b, the existence of both a witness for 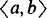 and a witness for
and a witness for 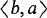 . The formulas we consider demand less: they require, for any elements a and b, a witness for the unordered pair {a, b}, that is, a witness either for
. The formulas we consider demand less: they require, for any elements a and b, a witness for the unordered pair {a, b}, that is, a witness either for 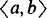 or for
or for 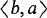 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 2
- Cited by

