Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-26T20:57:04.279Z Has data issue: false hasContentIssue false
  • English
  • Français

Decisive creatures and large continuum

Published online by Cambridge University Press:  12 March 2014

Jakob Kellner  and
Saharon Shelah
Jakob Kellner
Affiliation:
Kurt Gödel Research Center for Mathematical Logic, Universität Wien, Währinger Straße 25, 1090 Wien, Austria, E-mail: kellner@fsmat.at, URL: http://www.logic.univie.ac.at/~kellner
Saharon Shelah
Affiliation:
Einstein Institute of Mathematics, Edmond J. Safra Campus, Givat Ram, The Hebrew University of Jerusalem, Jerusalem, 91904, Israel Department of Mathematics, Rutgers University, New Brunswick, Nj 08854, USA, E-mail: shelah@math.huji.ac.il, URL: http://shelah.logic.at
Get access Rights & Permissions [Opens in a new window]

Abstract

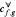For f, g ∈ ωω let be the minimal number of uniform g-splitting trees (or: Slaloms) to cover the uniform f-splitting tree, i.e., for every branch v of the f-tree, one of the g-trees contains v. 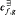is the dual notion: For every branch v, one of the g-trees guesses v(m) infinitely often.

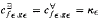It is consistent that for ℵ1 many pairwise different cardinals κ∊ and suitable pairs (f∊, g∊).

For the proof we use creatures with sufficient bigness and halving. We show that the lim-inf creature forcing satisfies fusion and pure decision. We introduce decisiveness and use it to construct a variant of the countable support iteration of such forcings, which still satisfies fusion and pure decision.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 74 , Issue 1 , March 2009 , pp. 73 - 104
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Baumgartner, James E., Iterated forcing, Surveys in set theory, London Mathematical Society Lecture Note Series, vol. 87, Cambridge University Press, Cambridge, 1983, pp. 1–59.Google Scholar
[2]Goldstern, Martin, Tools for your forcing construction, Set theory of the reals (Ramat Gan, 1991), Israel Mathematical Conference Proceedings, vol. 6, Bar-Ilan University, Ramat Gan, 1993, available at http://info.tuwien.ac.at/goldstern/, pp. 305–360.Google Scholar
[3]Goldstern, Martin and Shelah, Saharon, Many simple cardinal invariants, Archive for Mathematical Logic, vol. 32 (1993), no. 3, pp. 203–221.CrossRefGoogle Scholar
[4]Kellner, Jakob, Even more simple cardinal invariants, Archive for Mathematical Logic, vol. 47 (2008), no. 5, pp. 503–515.CrossRefGoogle Scholar
[5]Rosłanowski, Andrzej and Shelah, Saharon, Norms on possibilities. I. Forcing with trees and creatures, Memoirs of the American Mathematical Society, vol. 141 (1999), no. 671, pp. xii + 167.CrossRefGoogle Scholar
[6]Shelah, Saharon, Proper and improper forcing, second ed., Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1998.CrossRefGoogle Scholar