Hostname: page-component-76fb5796d-r6qrq Total loading time: 0 Render date: 2024-04-30T06:02:59.367Z Has data issue: false hasContentIssue false
  • English
  • Français

Definable incompleteness and Friedberg splittings

Published online by Cambridge University Press:  12 March 2014

Russell Miller
Russell Miller*
Affiliation:
Department of Mathematics, University of Chicago, Chicago, Illinois 60637, USA
*
Department of Mathematics, Cornell University, Ithaca, New York 14853, USA, E-mail: russell@math.cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a property R(A0, A1) in the partial order 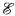of computably enumerable sets under inclusion, and prove that R implies that A0 is noncomputable and incomplete. Moreover, the property is nonvacuous. and the A0 and A1 which we build satisfying R form a Friedberg splitting of their union A, with A1 prompt and A promptly simple. We conclude that A0 and A1 lie in distinct orbits under automorphisms of 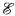, yielding a strong answer to a question previously explored by Downey, Stob, and Soare about whether halves of Friedberg splittings must lie in the same orbit.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 2 , June 2002 , pp. 679 - 696
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cholak, P., Automorphisms of the lattice of recursively enumerable sets, Memoirs of the American Mathematical Society, vol. 113 (1995), no. 541.CrossRefGoogle Scholar
[2]Cholak, P., Downey, R., and Stob, M., Automorphisms of the lattice of recursively enumerable sets: Promptly simple sets, Transactions of the American Mathematical Society, vol. 332 (1993). pp. 555–569.CrossRefGoogle Scholar
[3]Downey, R. and Stob, M., Jumps of hemimaximal sets, Zeitschrift für Math. Logik Grundlagen, vol. 37 (1991), pp. 113–120.CrossRefGoogle Scholar
[4]Downey, R. and Stob, M., Automorphisms of the lattice of recursively enumerable sets: Orbits, Advances in Mathematics, vol. 92 (1992), pp. 237–265.CrossRefGoogle Scholar
[5]Downey, R. and Stob, M., Friedberg splittings of recursively enumerable sets, Annals of Pure and Applied Logic, vol. 59 (1993), pp. 175–199.CrossRefGoogle Scholar
[6]Friedberg, R. M., Two recursively enumerable sets of incomparable degrees of unsolvability, Proceedings of the National Academy of Sciences, USA, vol. 43 (1957), pp. 236–238.CrossRefGoogle ScholarPubMed
[7]Harrington, L. and Soare, R. I., Post's program and incomplete recursively enumerable sets, Proceedings of the National Academy of Sciences, USA, vol. 88 (1991), pp. 10242–10246.CrossRefGoogle ScholarPubMed
[8]Harrington, L. and Soare, R. I., The Δ30-automorphism method and noninvariant classes of degrees, Journal of the American Mathematical Society, vol. 9 (1996). pp. 617–666.CrossRefGoogle Scholar
[9]Harrington, L. and Soare, R. I., Definable properties of the computably enumerable sets, Annals of Pure and Applied Logic, vol. 94 (1998), pp. 97–125.CrossRefGoogle Scholar
[10]Jockusch, C. G. Jr., Review of Lerman [11], Mathematical Reviews, vol. 45 (1973). #3200.Google Scholar
[11]Lerman, M., Some theorems on r-maximal sets and major subsets of recursively enumerable sets, this Journal, vol. 36 (1971). pp. 193–215.Google Scholar
[12]Maass, W. and Stob, M., The intervals of the lattice of recursively enumerable sets determined by major subsets, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 189–212.CrossRefGoogle Scholar
[13]Muchnik, A. A., On the unsolvability of the problem of reducibilily in the theory of algorithms, Dokl. Akad. Nauk SSSR, N. S., vol. 109 (1956). pp. 194–197, in Russian.Google Scholar
[14]Myhill, J., The lattice of recursively enumerable sets, this Journal, vol. 21 (1956). pp. 215, 220.Google Scholar
[15]Rogers, H. Jr., Theory of recursive functions and effective computability, The MIT Press, Cambridge, Massachusetts, 1987.Google Scholar
[16]Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, New York, 1987.CrossRefGoogle Scholar