Article contents
α-degrees of α-theories1
Published online by Cambridge University Press: 12 March 2014
Extract
Let α be a limit ordinal with the property that any “recursive” function whose domain is a proper initial segment of α has its range bounded by α. α is then called admissible (in a sense to be made precise later) and a recursion theory can be developed on it (α-recursion theory) by providing the generalized notions of α-recursively enumerable, α-recursive and α-finite. Takeuti [12] was the first to study recursive functions of ordinals, the subject owing its further development to Kripke [7], Platek [8], Kreisel [6], and Sacks [9].
Infinitary logic on the other hand (i.e., the study of languages which allow expressions of infinite length) was quite extensively studied by Scott [11], Tarski, Kreisel, Karp [5] and others. Kreisel suggested in the late '50's that these languages (even 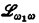 which allows countable expressions but only finite quantification) were too large and that one should only allow expressions which are, in some generalized sense, finite. This made the application of generalized recursion theory to the logic of infinitary languages appear natural. In 1967 Barwise [1] was the first to present a complete formalization of the restriction of
which allows countable expressions but only finite quantification) were too large and that one should only allow expressions which are, in some generalized sense, finite. This made the application of generalized recursion theory to the logic of infinitary languages appear natural. In 1967 Barwise [1] was the first to present a complete formalization of the restriction of 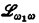 to an admissible fragment
to an admissible fragment 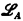 (A a countable admissible set) and to prove that completeness and compactness hold for it. [2] is an excellent reference for a detailed exposition of admissible languages.
(A a countable admissible set) and to prove that completeness and compactness hold for it. [2] is an excellent reference for a detailed exposition of admissible languages.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
Footnotes
This research was done as part of the author's Doctoral Dissertation (Cornell University, 1971) which was partially supported by NSF grant GP-22719 and was directed by Professor Anil Nerode, to whom, along with Professors R. Platek and M. D. Morley, the author expresses his thanks for numerous conversations. The author also wishes to thank the referee of this paper for his valuable suggestions.
References
REFERENCES
- 1
- Cited by

