Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Baldwin, John T.
and
Kolesnikov, Alexei
2009.
Categoricity, amalgamation, and tameness.
Israel Journal of Mathematics,
Vol. 170,
Issue. 1,
p.
411.
Lieberman, Michael
2011.
A topology for galois types in abstract elementary classes.
Mathematical Logic Quarterly,
Vol. 57,
Issue. 2,
p.
204.
2011.
Issue Information.
Mathematical Logic Quarterly,
Vol. 57,
Issue. 2,
Boney, Will
2014.
Tameness and extending frames.
Journal of Mathematical Logic,
Vol. 14,
Issue. 02,
p.
1450007.
Vasey, Sebastien
2016.
Building independence relations in abstract elementary classes.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 11,
p.
1029.
Vasey, Sebastien
2017.
Shelah's eventual categoricity conjecture in universal classes: Part I.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 9,
p.
1609.
Ghadernezhad, Zaniar
and
Villaveces, Andrés
2018.
The small index property for homogeneous models in AEC’s.
Archive for Mathematical Logic,
Vol. 57,
Issue. 1-2,
p.
141.
Shelah, Saharon
and
Vasey, Sebastien
2018.
Abstract elementary classes stable in ℵ0.
Annals of Pure and Applied Logic,
Vol. 169,
Issue. 7,
p.
565.
Vasey, Sebastien
2018.
Shelah's eventual categoricity conjecture in tame abstract elementary classes with primes.
Mathematical Logic Quarterly,
Vol. 64,
Issue. 1-2,
p.
25.
Vasey, Sebastien
2018.
Quasiminimal abstract elementary classes.
Archive for Mathematical Logic,
Vol. 57,
Issue. 3-4,
p.
299.
Ackerman, Nathanael
Boney, Will
and
Vasey, Sebastien
2019.
Categoricity in multiuniversal classes.
Annals of Pure and Applied Logic,
Vol. 170,
Issue. 11,
p.
102712.
Lieberman, Michael
Rosický, Jiří
and
Vasey, Sebastien
2019.
Internal sizes in μ-abstract elementary classes.
Journal of Pure and Applied Algebra,
Vol. 223,
Issue. 10,
p.
4560.
Mazari-Armida, Marcos
2020.
Algebraic description of limit models in classes of abelian groups.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 1,
p.
102723.
Shelah, Saharon
and
Villaveces, Andrés
2021.
The Hart-Shelah example, in stronger logics.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 6,
p.
102958.
Grossberg, Rami
and
Mazari-Armida, Marcos
2021.
Simple-like independence relations in abstract elementary classes.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 7,
p.
102971.
VASEY, SEBASTIEN
2022.
ON CATEGORICITY IN SUCCESSIVE CARDINALS.
The Journal of Symbolic Logic,
Vol. 87,
Issue. 2,
p.
545.
MAZARI-ARMIDA, MARCOS
and
YANG, WENTAO
2024.
BUILDING MODELS IN SMALL CARDINALS IN LOCAL ABSTRACT ELEMENTARY CLASSES.
The Journal of Symbolic Logic,
p.
1.
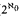 , ∞)-tame; Theorem 3.3. It is consistent with ZFC that there is an AEC with amalgamation which is not (≤ ℵ2, ≤ ℵ2)-compact.
, ∞)-tame; Theorem 3.3. It is consistent with ZFC that there is an AEC with amalgamation which is not (≤ ℵ2, ≤ ℵ2)-compact.
