Article contents
EXISTENCE OF MODELING LIMITS FOR SEQUENCES OF SPARSE STRUCTURES
Published online by Cambridge University Press: 07 March 2019
Abstract
A sequence of graphs is FO-convergent if the probability of satisfaction of every first-order formula converges. A graph modeling is a graph, whose domain is a standard probability space, with the property that every definable set is Borel. It was known that FO-convergent sequence of graphs do not always admit a modeling limit, but it was conjectured that FO-convergent sequences of sufficiently sparse graphs have a modeling limits. Precisely, two conjectures were proposed:
1. If a FO-convergent sequence of graphs is residual, that is if for every integer d the maximum relative size of a ball of radius d in the graphs of the sequence tends to zero, then the sequence has a modeling limit.
2. A monotone class of graphs
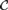 ${\cal C}$ has the property that every FO-convergent sequence of graphs from
${\cal C}$ has the property that every FO-convergent sequence of graphs from 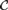 ${\cal C}$ has a modeling limit if and only if
${\cal C}$ has a modeling limit if and only if 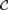 ${\cal C}$ is nowhere dense, that is if and only if for each integer p there is
${\cal C}$ is nowhere dense, that is if and only if for each integer p there is 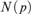 $N\left( p \right)$ such that no graph in
$N\left( p \right)$ such that no graph in 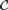 ${\cal C}$ contains the pth subdivision of a complete graph on
${\cal C}$ contains the pth subdivision of a complete graph on 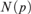 $N\left( p \right)$ vertices as a subgraph.
$N\left( p \right)$ vertices as a subgraph.
In this article we prove both conjectures. This solves some of the main problems in the area and among others provides an analytic characterization of the nowhere dense–somewhere dense dichotomy.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
A correction has been issued for this article:
- 5
- Cited by
Linked content
Please note a has been issued for this article.

