Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shelah, Saharon
2003.
Logical dreams.
Bulletin of the American Mathematical Society,
Vol. 40,
Issue. 2,
p.
203.
Shelah, Saharon
2009.
The Erdős–Rado Arrow for Singular Cardinals.
Canadian Mathematical Bulletin,
Vol. 52,
Issue. 1,
p.
127.
Benhamou, Tom
Garti, Shimon
and
Poveda, Alejandro
2025.
Galvin’s property at large cardinals and an application to partition calculus.
Israel Journal of Mathematics,


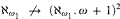 and consistently,
and consistently, 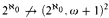 .
.