Article contents
FINDING DESCENDING SEQUENCES THROUGH ILL-FOUNDED LINEAR ORDERS
Published online by Cambridge University Press: 01 February 2021
Abstract
In this work we investigate the Weihrauch degree of the problem Decreasing Sequence ( $\mathsf {DS}$) of finding an infinite descending sequence through a given ill-founded linear order, which is shared by the problem Bad Sequence (
$\mathsf {DS}$) of finding an infinite descending sequence through a given ill-founded linear order, which is shared by the problem Bad Sequence (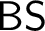 $\mathsf {BS}$) of finding a bad sequence through a given non-well quasi-order. We show that
$\mathsf {BS}$) of finding a bad sequence through a given non-well quasi-order. We show that 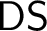 $\mathsf {DS}$, despite being hard to solve (it has computable inputs with no hyperarithmetic solution), is rather weak in terms of uniform computational strength. To make the latter precise, we introduce the notion of the deterministic part of a Weihrauch degree. We then generalize
$\mathsf {DS}$, despite being hard to solve (it has computable inputs with no hyperarithmetic solution), is rather weak in terms of uniform computational strength. To make the latter precise, we introduce the notion of the deterministic part of a Weihrauch degree. We then generalize 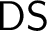 $\mathsf {DS}$ and
$\mathsf {DS}$ and 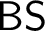 $\mathsf {BS}$ by considering
$\mathsf {BS}$ by considering  $\boldsymbol {\Gamma }$-presented orders, where
$\boldsymbol {\Gamma }$-presented orders, where  $\boldsymbol {\Gamma }$ is a Borel pointclass or
$\boldsymbol {\Gamma }$ is a Borel pointclass or 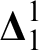 $\boldsymbol {\Delta }^1_1$,
$\boldsymbol {\Delta }^1_1$, 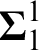 $\boldsymbol {\Sigma }^1_1$,
$\boldsymbol {\Sigma }^1_1$, 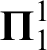 $\boldsymbol {\Pi }^1_1$. We study the obtained
$\boldsymbol {\Pi }^1_1$. We study the obtained 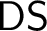 $\mathsf {DS}$-hierarchy and
$\mathsf {DS}$-hierarchy and  $\mathsf {BS}$-hierarchy of problems in comparison with the (effective) Baire hierarchy and show that they do not collapse at any finite level.
$\mathsf {BS}$-hierarchy of problems in comparison with the (effective) Baire hierarchy and show that they do not collapse at any finite level.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Association for Symbolic Logic 2021
References
- 9
- Cited by


