Article contents
THE FLUTED FRAGMENT REVISITED
Published online by Cambridge University Press: 06 June 2019
Abstract
We study the fluted fragment, a decidable fragment of first-order logic with an unbounded number of variables, motivated by the work of W. V. Quine. We show that the satisfiability problem for this fragment has nonelementary complexity, thus refuting an earlier published claim by W. C. Purdy that it is in NExpTime. More precisely, we consider 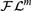 ${\cal F}{{\cal L}^m}$, the intersection of the fluted fragment and the m-variable fragment of first-order logic, for all
${\cal F}{{\cal L}^m}$, the intersection of the fluted fragment and the m-variable fragment of first-order logic, for all 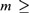 $m \ge 1$. We show that, for
$m \ge 1$. We show that, for 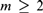 $m \ge 2$, this subfragment forces
$m \ge 2$, this subfragment forces 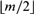 $\left\lfloor {m/2} \right\rfloor$-tuply exponentially large models, and that its satisfiability problem is
$\left\lfloor {m/2} \right\rfloor$-tuply exponentially large models, and that its satisfiability problem is 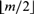 $\left\lfloor {m/2} \right\rfloor$-NExpTime-hard. We further establish that, for
$\left\lfloor {m/2} \right\rfloor$-NExpTime-hard. We further establish that, for 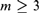 $m \ge 3$, any satisfiable
$m \ge 3$, any satisfiable 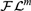 ${\cal F}{{\cal L}^m}$-formula has a model of at most (
${\cal F}{{\cal L}^m}$-formula has a model of at most (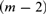 $m - 2$)-tuply exponential size, whence the satisfiability (= finite satisfiability) problem for this fragment is in (
$m - 2$)-tuply exponential size, whence the satisfiability (= finite satisfiability) problem for this fragment is in (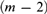 $m - 2$)-NExpTime. Together with other, known, complexity results, this provides tight complexity bounds for
$m - 2$)-NExpTime. Together with other, known, complexity results, this provides tight complexity bounds for 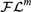 ${\cal F}{{\cal L}^m}$ for all
${\cal F}{{\cal L}^m}$ for all 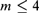 $m \le 4$.
$m \le 4$.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 7
- Cited by

