Hostname: page-component-7dd5485656-wlg5v Total loading time: 0 Render date: 2025-10-31T03:06:20.103Z Has data issue: false hasContentIssue false
  • English
  • Français

FORCING AXIOMS AND THE DEFINABILITY OF THE NONSTATIONARY IDEAL ON THE FIRST UNCOUNTABLE

Part of: Set theory

Published online by Cambridge University Press:  19 June 2023

STEFAN HOFFELNER Open the ORCID record for STEFAN HOFFELNER [Opens in a new window] ,
PAUL LARSON ,
RALF SCHINDLER  and
LIUZHEN WU
STEFAN HOFFELNER*
Affiliation:
INSTIUT FÜR MATHEMATISCHE LOGIK UND GRUNDLAGENFORSCHUNG WWU MÜNSTER, EINSTEINSTRAßE 62 48149 MÜNSTER, GERMANY
PAUL LARSON
Affiliation:
DEPARTMENT OF MATHEMATICS, MIAMI UNIVERSITY 301 S. PATTERSON AVENUE, 123 BACHELOR HALL OXFORD, OH 45056, USA E-mail: larsonpb@miamioh.edu URL: https://www.users.miamioh.edu/larsonpb/
RALF SCHINDLER
Affiliation:
INSTITUT FÜR MATHEMATISCHE LOGIK UND GRUNDLAGENFORSCHUNG UNIVERSITÄT MÜNSTER EINSTEINSTRAßE 62 48149 MÜNSTER, GERMANY E-mail: rds@uni-muenster.de URL: https://ivv5hpp.uni-muenster.de/u/rds/
LIUZHEN WU
Affiliation:
INSTITUTE OF MATHEMATICS, CHINESE ACADEMY OF SCIENCES NO. 55, EAST ZHONG GUAN CUN ROAD BEIJING 100190, CHINA E-mail: lzwu@math.ac.cn URL: http://people.ucas.ac.cn/lzwu
*
E-mail: stefan.hoffelner@gmx.at
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that under 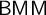$\mathsf {BMM}$ and “there exists a Woodin cardinal,$"$ the nonstationary ideal on 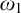$\omega _1$ cannot be defined by a 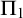$\Pi _1$ formula with parameter 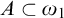$A \subset \omega _1$. We show that the same conclusion holds under the assumption of Woodin’s $(\ast )$-axiom. We further show that there are universes where 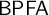$\mathsf {BPFA}$ holds and 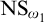$\text {NS}_{\omega _1}$ is 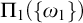$\Pi _1(\{\omega _1\})$-definable. Lastly we show that if the canonical inner model with one Woodin cardinal 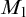$M_1$ exists, there is a generic extension of 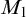$M_1$ in which 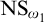$\text {NS}_{\omega _1}$ is saturated and 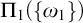$\Pi _1(\{ \omega _1\} )$-definable, and 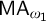$\mathsf {MA_{\omega _1}}$ holds.

Keywords

nonstationary idealdefinabilityforcing axioms

MSC classification

Primary: 03E35: Consistency and independence results
Secondary: 03E45: Inner models, including constructibility, ordinal definability, and core models 03E55: Large cardinals 03E57: Generic absoluteness and forcing axioms

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 4 , December 2024 , pp. 1641 - 1658
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bagaria, J., Generic absoluteness and forcing axioms , Models, Algebras, and Proofs (X. Caicedo and C. H. Montenegro, editors), Lecture Notes in Pure and Applied Mathematics, vol. 203, Dekker, New York, 1999, pp. 1–12.Google Scholar
Caicedo, A. and Velickovic, B., The bounded proper forcing axiom and well orderings of the reals . Mathematical Research Letters , vol. 13 (2006), nos. 2–3, pp. 393–408.CrossRefGoogle Scholar
Foreman, M. and Magidor, M., Mutually stationary sequences of sets and the non-saturation of the non-stationary ideal on ${P}_{\kappa}(\lambda)$ . Acta Mathematica , vol. 186 (2001), no. 2, pp. 271–300.CrossRefGoogle Scholar
Goldstern, M. and Shelah, S., The bounded proper forcing axiom , this Journal, vol. 60 (1995), no. 1, pp. 58–73.Google Scholar
Harrington, L., Long projective wellorderings . Annals of Mathematical Logic , vol. 12 (1977), no. 1, pp. 1–24.CrossRefGoogle Scholar
Hoffelner, S., ${NS}_{\omega_1}$ ${\varDelta}_1$ -definable and saturated , this Journal, vol. 86 (2021), no. 1, pp. 25–59.Google Scholar
Hoffelner, S., Larson, P. B., Schindler, R., and Wu, L., $\mathsf{PFA}$ and the definability of the nonstationary ideal, in preparation.Google Scholar
Jech, T., Set Theory: The Third Millennium Edition , Springer, Berlin–Heidelberg, 2003.Google Scholar
Larson, P. B., The Stationary Tower. Notes on a Course by W. Hugh Woodin , University Lecture Series, vol. 32, American Mathematical Society, Providence, 2004.Google Scholar
Larson, P. B., Forcing over models of determinacy , Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Dordrecht, 2010, pp. 2121–2177.CrossRefGoogle Scholar
Lücke, P., Schindler, R., and Schlicht, P.,  ${\varSigma}_1(\kappa)$ -definable subsets of $H({\kappa}^{+})$ , this Journal, vol. 82 (2017), no. 3, pp. 1106–1131.Google Scholar
Miyamoto, T., On iterating semiproper preorders , this Journal, vol. 67 (2002), pp. 1431–1468.Google Scholar
Moore, J. T., Set mapping reflection . Journal of Mathematical Logic , vol. 5 (2005), no. 1, pp. 87–97.CrossRefGoogle Scholar
Schindler, R. and Sun, X., $\mathsf{MM}$ and the definability of ${\mathrm{NS}}_{\omega_1}\kern-1.2pt$ , preprint, 2022.Google Scholar
Shelah, S., Proper and Improper Forcing , second ed., Perspectives in Mathematical Logic, vol. 5, Springer, Berlin, 1998, xlviii + 1020 pp.CrossRefGoogle Scholar
Taylor, A., Regularity properties of ideals and ultrafilters . Annals of Mathematical Logic , vol. 16 (1979), pp. 33–55.CrossRefGoogle Scholar
Todorcevic, S., Localized reflection and fragments of PFA , Set Theory (Piscataway, NJ, 1999) (S. Thomas, editor), DIMACS Series in Discrete Mathematics and Theoretical Computer Science, vol. 58, American Mathematics Society, Providence, 2002, pp. 135–148.CrossRefGoogle Scholar
Todorcevic, S., Generic absoluteness and the continuum . Mathematical Research Letters , vol. 9 (2002), no. 4, 465–471.CrossRefGoogle Scholar
Woodin, H. W., The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal , De Gruyter, Berlin–New York, 2001.Google Scholar