Hostname: page-component-5d84bcc8dc-b9bcm Total loading time: 0 Render date: 2026-09-11T23:28:15.037Z Has data issue: false hasContentIssue false
  • English
  • Français

Forcing the failure of CH by adding a real

Published online by Cambridge University Press:  12 March 2014

Saharon Shelah  and
Hugh Woodin
Saharon Shelah
Affiliation:
The Hebrew University, Jerusalem, Israel
Hugh Woodin
Affiliation:
California Institute of Technology, Pasadena, California 91125
Get access Rights & Permissions [Opens in a new window]

Extract

We prove several independence results relevant to an old question in the folklore of set theory. These results complement those in [Sh, Chapter XIII, §4]. The question is the following. Suppose V ⊨ “ZFC + CH” and r is a real not in V. Must V[r] ⊨ CH? To avoid trivialities assume = .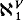

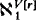We answer this question negatively. Specifically we find pairs of models (W, V) such that W ⊨ ZFC + CH, V = W[r], r a real, 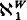= 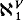and V ⊨ ¬CH. Actually we find a spectrum of such pairs using ZFC up to “ZFC + there exist measurable cardinals”. Basically the nicer the pair is as a solution, the more we need to assume in order to construct it.

The relevant results in [Sh, Chapter XIII] state that if a pair (of inner models) (W, V) satisfies (1) and (2) then there is an inaccessible cardinal in L; if in addition V ⊨ 2ℵ0 > ℵ2 then 0# exists; and finally if (W, V) satisfies (1), (2) and (3) with V ⊨ 2ℵ0 > ℵω, then there is an inner model with a measurable cardinal.

Definition 1. For a pair (W, V) we shall consider the following conditions:

(1) V = W[r], r a real, 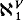= 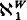, W ⊨ ZFC + CH but CH fails in V.

(2) W ⊨ GCH.

(3) W and V have the same cardinals.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 4 , December 1984 , pp. 1185 - 1189
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[BJW]Beller, A., Jensen, R. B. and Welch, P., Coding the universe, London Mathematical Society Lecture Note Series, no. 47, Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
[JS]Jensen, R. B. and Solovay, R., Some applications of almost disjoint sets, Mathematical logic and the foundations of set theory (proceedings of an international colloquium, Jerusalem, 1968; Bar-Hillel, Y., editor), North-Holland, Amsterdam, 1970, pp. 84–104.Google Scholar
[Sh]Shelah, S., Proper forcing, Lecture Notes in Mathematics, vol. 940, Springer-Verlag, Berlin, 1982.CrossRefGoogle Scholar