Article contents
The þ-function in λ-K-conversion
Published online by Cambridge University Press: 12 March 2014
Extract
In the theory of conversion it is important to have a formally defined function which assigns to any positive integer n the least integer not less than n which has a given property. The definition of such a formula is somewhat involved: I propose to give the corresponding formula in λ-K-conversion, which will (naturally) be much simpler. I shall in fact find a formula þ such that if T be a formula for which T(n) is convertible to a formula representing a natural number, whenever n represents a natural number, then þ(T, r) is convertible to the formula q representing the least natural number q, not less than r, for which T(q) conv 0.2 The method depends on finding a formula Θ with the property that Θ conv λu·u(Θ(u)), and consequently if M→Θ(V) then M conv V(M). A formula with this property is,
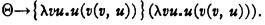
The formula þ will have the required property if þ(T, r) conv r when T(r) conv 0, and þ(T, r) conv þ(T, S(r)) otherwise. These conditions will be satisfied if þ(T, r) conv T(r, λx·þ(T, S(r)), r), i.e. if þ conv {λptr·t(r, λx·p(t, S(r)), r)}(þ). We therefore put,
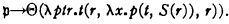
This enables us to define also a formula,
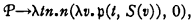
such that 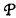 (T, n) is convertible to the formula representing the nth positive integer q for which T(q) conv 0.
(T, n) is convertible to the formula representing the nth positive integer q for which T(q) conv 0.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1937
References
1 Such a function was first defined by Kleene, S. C., A theory of positive integers in formal logic, American journal of mathematics, vol. 57 (1934), see p. 231 Google Scholar.
2 For the definition of λ-K-conversion see Kleene, S. C., λ-definability and recursiveness, Duke mathematical journal, vol. 2 (1936), pp. 340–353, footnote 12CrossRefGoogle Scholar. In λ-K-conversion we are able to define the formula 0 → λfx·x. The same paper of Kleene contains the definition of a formula L with a property similar to the essential property of Θ (p. 346).
3 “Convertible” and “conv” refer to λ-K-conversion throughout this note.
- 20
- Cited by

