Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-29T13:25:46.113Z Has data issue: false hasContentIssue false
  • English
  • Français

Incompatible Ω-Complete Theories

Published online by Cambridge University Press:  12 March 2014

Peter Koellner  and
W. Hugh Woodin
Peter Koellner
Affiliation:
Department of Philosophy, Harvard University, 25 Quincy Street, Cambridge, Ma 02138, USA, E-mail: koellner@fas.harvard.edu
W. Hugh Woodin
Affiliation:
Department of Mathematics, University of California, Berkeley, Berkeley, Ca 94720-3840, USA, E-mail: woodin@math.berkeley.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In 1985 the second author showed that if there is a proper class of measurable Woodin cardinals 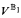and and 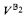are generic extensions of V satisfying CH then 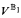and 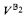agree on all Σ12-statements. In terms of the strong logic Ω-logic this can be reformulated by saying that under the above large cardinal assumption ZFC + CH is Ω-complete for Σ12. Moreover, CH is the unique Σ12-statement with this feature in the sense that any other Σ12-statement with this feature is Ω-equivalent to CH over ZFC. It is natural to look for other strengthenings of ZFC that have an even greater degree of Ω-completeness. For example, one can ask for recursively enumerable axioms A such that relative to large cardinal axioms ZFC + A is Ω-complete for all of third-order arithmetic. Going further, for each specifiable segment Vλ of the universe of sets (for example, one might take Vλ to be the least level that satisfies there is a proper class of huge cardinals), one can ask for recursively enumerable axioms A such that relative to large cardinal axioms ZFC + A is Ω-complete for the theory of Vλ. If such theories exist, extend one another, and are unique in the sense that any other such theory B with the same level of Ω-completeness as A is actually Ω-equivalent to A over ZFC, then this would show that there is a unique Ω-complete picture of the successive fragments of the universe of sets and it would make for a very strong case for axioms complementing large cardinal axioms. In this paper we show that uniqueness must fail. In particular, we show that if there is one such theory that Ω-implies CH then there is another that Ω-implies ¬-CH.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 74 , Issue 4 , December 2009 , pp. 1155 - 1170
Copyright
Copyright © Association for Symbolic Logic 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Abraham, Uri and Shelah, Saharon, Δ22 well-order of the reals and incompactness of L(QMM), Annals of Pure and Applied Logic, vol. 59 (1993), no. 1, pp. 1–32.CrossRefGoogle Scholar
[2]Bagaria, Joan, Castells, Neus, and Larson, Paul, An Ω-logic primer, Set theory (Bagaria, Joan and Todorcevic, Stevo, editors), Trends in Mathematics, Birkhäuser, Basel, 2006, pp. 1–28.CrossRefGoogle Scholar
[3]Davis, Morton, Infinite games of perfect information, Advances in game theory (Dresher, Melvin, Shapley, Lloyd S, and Tucker, Alan W., editors), Annals of Mathematical Studies, vol. 52, Princeton University Press, Princeton, 1964, pp. 85–101.Google Scholar
[4]Feferman, Solomon Jr., Dawson, John W., Kleene, Stephen C., Moore, Gregory H., Solovay, Robert M., and van Heijenoort, Jean (editors), Gödel, Kurt, Collected works, Volume II: Publications 1938–1974, Oxford University Press, New York and Oxford, 1990.Google Scholar
[5]Feng, Qi, Magidor, Menacham, and Woodin, W. Hugh, Universally Baire sets of reals, Set theory of the continuum (Judah, Haim, Just, Winfried, and Woodin, W. Hugh, editors), Mathematical Sciences Research Institute, vol. 26, Springer-Verlag, Berlin, 1992, pp. 203–242.CrossRefGoogle Scholar
[6]Gödel, Kurt, Remarks before the Princeton bicentennial conference on problems in mathematics, In Feferman et al. [4], pp. 150–153.CrossRefGoogle Scholar
[7]Hamkins, Joel David and Woodin, W. Hugh, Small forcing creates neither strong nor Woodin cardinals, Proceedings of the American Mathematical Society, vol. 128 (2000), no. 10, pp. 3025–3029.CrossRefGoogle Scholar
[8]Kanamori, Akihiro, The higher infinite: Large cardinals in set theory from their beginnings, second ed., Springer Monographs in Mathematics, Springer, Berlin, 2003.Google Scholar
[9]Koellner, Peter, On the question of absolute undecidability, Philosophia Mathematica, vol. 14 (2006), no. 2, pp. 153–188, Revised and reprinted in Kurt Gödel: Essays for his Centennial, edited by Solomon Feferman, Charles Parsons, and Stephen G. Simpson. Lecture Notes in Logic, 33. Association of Symbolic Logic, 2009.CrossRefGoogle Scholar
[10]Koellner, Peter, Truth in mathematics: The question of pluralism. New waves in philosophy of mathematics (Bueno, Otávio and Linnebo, Øystein, editors), New Waves in Philosophy, Palgrave Macmillan, 2009, Forthcoming.Google Scholar
[11]Larson, Paul, The stationary tower: Notes on a course by W. Hugh Woodin, University Lecture Series, vol. 32, American Mathematical Society, 2004.Google Scholar
[12]Larson, Paul, Ketchersid, Richard, and Zapletal, Jindrich, Regular embeddings of the stationary tower and Woodin's Σ22 maximality theorem, preprint, 2008.Google Scholar
[13]Laver, Richard, Certain very large cardinals are not created in small forcing extensions. Annals of Pure and Applied Logic, vol. 149 (2007), no. 1-3, pp. 1–6.CrossRefGoogle Scholar
[14]Lévy, Azriel and Solovay, Robert M., Measurable cardinals and the continuum hypothesis, Israel Journal of Mathematics, vol. 5 (1967), pp. 234–248.CrossRefGoogle Scholar
[15]Martin, Donald A. and Steel, John R., The extent of scales in L(ℝ), Cabal seminar 79–81 (Kechris, Alexander S., Martin, Donald A., and Moschovakis, Yiannis S., editors), Lecture Notes in Mathematics, no. 1019, Springer-Verlag, Berlin, 1983, pp. 86–96.CrossRefGoogle Scholar
[16]Martin, Donald A. and Steel, John R., A proof of projective determinacy, Journal of the American Mathematical Society, vol. 2 (1989), no. 1, pp. 71–125.CrossRefGoogle Scholar
[17]Mycielski, Jan and Swierczkowski, Stanislaw, On the Lebesgue measurability and the axiom of determinateness, Fundament a Mathematicae, vol. 54 (1964), pp. 67–71.CrossRefGoogle Scholar
[18]Paris, Jeff and Harrington, Leo, A mathematical incompleteness in Peano Arithmetic, Handbook of mathematical logic (Barwise, Jon, editor), Studies in Logic and the Foundations of Mathematics, vol. 90, Elsevier, Amsterdam, 1977, pp. 1133–1142.CrossRefGoogle Scholar
[19]Shelah, Saharon and Woodin, W. Hugh, Large cardinals imply that every reasonably definable set of reals is Lebesgue measurable, Israel Journal of Mathematics, vol. 70 (1990), pp. 381–394.CrossRefGoogle Scholar
[20]Woodin, W. Hugh, Σ12 absoluteness, unpublished, 05 1985.Google Scholar
[21]Woodin, W. Hugh,Supercompact cardinals, sets of reals, and weakly homogeneous trees, Proceedings of the National Academy of Sciences, vol. 85 (1988), no. 18, pp. 6587–6591.CrossRefGoogle ScholarPubMed
[22]Woodin, W. Hugh,The axiom of determinacy, forcing axioms, and the nonstationary ideal, de Gruyter, Series in Logic and its Applications, vol. 1, de Gruyter, Berlin, 1999.CrossRefGoogle Scholar
[23]Woodin, W. Hugh,Beyond absoluteness, Proceedings of the International Congress of Mathematicians, (Beijing, 2002), vol. I, Higher Education Press, Beijing, 2002, pp. 515–524.Google Scholar
[24]Woodin, W. Hugh,Suitable Extender Sequences, To appear, 2009.CrossRefGoogle Scholar