Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1978.
Classification Theory.
Vol. 92,
Issue. ,
p.
684.
Shelah, S.
1981.
Free limits of forcing and more on Aronszajn trees.
Israel Journal of Mathematics,
Vol. 38,
Issue. 4,
p.
315.
Shelah, Saharon
1981.
Iterated forcing and changing cofinalities.
Israel Journal of Mathematics,
Vol. 40,
Issue. 1,
p.
1.
Shelah, Saharon
1983.
Lifting problem of the measure algebra.
Israel Journal of Mathematics,
Vol. 45,
Issue. 1,
p.
90.
Shelah, Saharon
1984.
On universal graphs without instances of CH.
Annals of Pure and Applied Logic,
Vol. 26,
Issue. 1,
p.
75.
Baldwin, John T.
1987.
Classification Theory.
Vol. 1292,
Issue. ,
p.
1.
Shelah, Saharon
1987.
Classification Theory.
Vol. 1292,
Issue. ,
p.
264.
Shelah, Saharon
1990.
Universal graphs without instances of CH: Revisited.
Israel Journal of Mathematics,
Vol. 70,
Issue. 1,
p.
69.
Shelah, Saharon
1991.
Reflecting stationary sets and successors of singular cardinals.
Archive for Mathematical Logic,
Vol. 31,
Issue. 1,
p.
25.
Kojman, Menachem
and
Shelah, Saharon
1992.
The universality spectrum of stable unsuperstable theories.
Annals of Pure and Applied Logic,
Vol. 58,
Issue. 1,
p.
57.
Judah, H.
and
Shelah, S.
1994.
Killing Luzin and Sierpiński sets.
Proceedings of the American Mathematical Society,
Vol. 120,
Issue. 3,
p.
917.
Berarducci, Alessandro
Dikranjan, Dikran
and
Pelant, Jan
2002.
Functions with distant fibers and uniform continuity.
Topology and its Applications,
Vol. 121,
Issue. 1-2,
p.
3.
Džamonja, Mirna
and
Shelah, Saharon
2004.
On the existence of universal models.
Archive for Mathematical Logic,
Vol. 43,
Issue. 7,
p.
901.
Džamonja, Mirna
2005.
Club Guessing and the Universal Models.
Notre Dame Journal of Formal Logic,
Vol. 46,
Issue. 3,
Larson, Jean A.
2005.
Ramsey Theory for Countable Binary Homogeneous Structures.
Notre Dame Journal of Formal Logic,
Vol. 46,
Issue. 3,
Thompson, Katherine
2006.
Universality for Orders and Graphs Which Omit Large Substructures.
Notre Dame Journal of Formal Logic,
Vol. 47,
Issue. 2,
Kojman, Menachem
and
Shelah, Saharon
2006.
Almost isometric embedding between metric spaces.
Israel Journal of Mathematics,
Vol. 155,
Issue. 1,
p.
309.
Burke, Maxim R.
2007.
Large entire cross-sections of second category sets in Rn+1.
Topology and its Applications,
Vol. 154,
Issue. 1,
p.
215.
Burke, Maxim
2009.
Entire functions mapping uncountable dense sets of reals onto each other monotonically.
Transactions of the American Mathematical Society,
Vol. 361,
Issue. 6,
p.
2871.
Burke, Maxim R.
2009.
Simultaneous approximation and interpolation of increasing functions by increasing entire functions.
Journal of Mathematical Analysis and Applications,
Vol. 350,
Issue. 2,
p.
845.

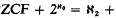 there is a universal linear order of power ℵ
there is a universal linear order of power ℵ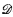 -properness for various filters and prove the consistency with G.C.H. of an axiom implying SH (for ℵ
-properness for various filters and prove the consistency with G.C.H. of an axiom implying SH (for ℵ