Hostname: page-component-7bb8b95d7b-w7rtg Total loading time: 0 Render date: 2024-09-16T20:55:03.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Isomorphisms and nonisomorphisms of graph models

Published online by Cambridge University Press:  12 March 2014

Harold Schellinx
Harold Schellinx*
Affiliation:
Department of Mathematics and Computer Science, University of Amsterdam, Amsterdam, The Netherlands
Get access Rights & Permissions [Opens in a new window]

Abstract

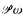In this paper the existence or nonexistence of isomorphic mappings between graph models for the untyped lambda calculus is studied. It is shown that Engeler's is DA completely determined, up to isomorphism, by the cardinality of its ‘atom-set’ A. A similar characterization is given for a collection of graph models of the -type; from this some propositions regarding automorphisms are obtained. Also we give an indication of the complexity of the first-order theory of graph models by showing that the second-order theory of first-order definable elements of a graph model is first-order expressable in the model.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 1 , March 1991 , pp. 227 - 249
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BaBo]Baeten, J. and Boerboom, R., Ω can be anything it shouldn't be, Indagationes Mathematicae, vol. 41 (1979), pp. 111–120.CrossRefGoogle Scholar
[Ba]Barendregt, H. P., The lambda calculus. Its syntax and semantics, North-Holland, Amsterdam, 1984.Google Scholar
[Lo]Longo, G., Set-theoretical models of λ-caiculus: theories, expansions, isomorphism, Annals of Pure and Applied Logic, vol. 24 (1983), pp. 153–188.CrossRefGoogle Scholar