Article contents
Models of arithmetic and closed ideals
Published online by Cambridge University Press: 12 March 2014
Extract
A set J of Turing degrees is called an ideal if (1) J ≠ ∅, (2) for any pair of degrees ã, 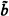 , if ã,
, if ã, 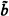 ϵ J, then ã ⋃
ϵ J, then ã ⋃ 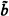 ϵJ, and (3) for any ⋃ ϵ J and any
ϵJ, and (3) for any ⋃ ϵ J and any 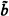 , if
, if 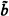 < ⋃, then
< ⋃, then 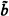 ϵ J. A set J of degrees is said to be closed if for any theory T with a set of axioms of degree in J, T has a completion of degree in J.
ϵ J. A set J of degrees is said to be closed if for any theory T with a set of axioms of degree in J, T has a completion of degree in J.
Closed ideals of degrees arise naturally in the following way. If 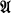 is a recursively saturated structure, let I(
is a recursively saturated structure, let I(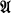 ) = {
) = {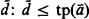 for some ā ϵ
for some ā ϵ 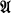 }. Let D(
}. Let D(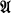 ) = {
) = {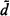 :
: 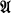 is recursive in d-saturated}. (Recursive in d-saturation is defined like recursive saturation except that the sets of formulas considered are recursive in d.) These two sets of degrees were investigated in [2]. It was shown that if
is recursive in d-saturated}. (Recursive in d-saturation is defined like recursive saturation except that the sets of formulas considered are recursive in d.) These two sets of degrees were investigated in [2]. It was shown that if 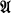 is a recursively saturated model of P, Pr = Th(ω, +), or Pr′ = Th(Z, +, 1), then I(
is a recursively saturated model of P, Pr = Th(ω, +), or Pr′ = Th(Z, +, 1), then I(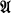 ) = D(
) = D(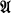 ), and this set is a closed ideal. Any closed ideal J can be represented as I(
), and this set is a closed ideal. Any closed ideal J can be represented as I(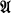 ) = D(
) = D(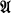 ) for some recursively saturated model
) for some recursively saturated model 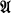 of Pr′. For sets J of power at most ℵ1, Pr′ can be replaced by P.
of Pr′. For sets J of power at most ℵ1, Pr′ can be replaced by P.
Assuming CH, all closed ideals have power at most ℵ1, but if CH fails, there are closed ideals of power greater than ℵ1, and it is not known whether these can be represented as I(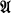 ) = D(
) = D(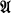 ) for a recursively saturated model
) for a recursively saturated model 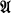 of P.
of P.
In the present paper, it will first be shown that information about representation of closed ideals provides new information about an old problem of MacDowell and Specker [6] and extends an old result of Scott [8] in a natural way. It will also be shown that the representation results from [2] answer a problem of Friedman [1]. This part of the paper is aimed at convincing the reader that representation problems are worth investigating.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1982
References
REFERENCES
- 8
- Cited by

