Article contents
More on proper forcing
Published online by Cambridge University Press: 12 March 2014
Extract
§1. A counterexample and preservation of “proper + X”.
Theorem. Suppose V satisfies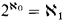 ,
, 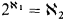 , and for some A ⊆ ω1, every B ⊆ ω1, belongs to L[A].
, and for some A ⊆ ω1, every B ⊆ ω1, belongs to L[A].
Then we can define a countable support iteration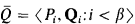 such that the following conditions hold:
such that the following conditions hold:
a) EachQiis proper and ⊩Pi “Qi, has power ℵ1”.
b) Each Qi is 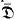 -complete for some simple ℵ1-completeness system.
-complete for some simple ℵ1-completeness system.
c) Forcing with Pα = Lim 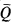 adds reals.
adds reals.
Proof. We shall define Qi by induction on i so that conditions a) and b) are satisfied, and Ci, is a Qi-name of a closed unbounded subset of ω1. Let 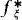 : ξ < ω1› ∈ L[A] be a list of all functions f which are from δ to δ for some δ < ω1 and let h: ω1 → ω1, h ∈ L[A], be defined by h(α) = Min{β: β > α and Lβ[A]⊨ “∣α∣ = ℵ0”}.
: ξ < ω1› ∈ L[A] be a list of all functions f which are from δ to δ for some δ < ω1 and let h: ω1 → ω1, h ∈ L[A], be defined by h(α) = Min{β: β > α and Lβ[A]⊨ “∣α∣ = ℵ0”}.
Suppose we have defined Qj for every j < i; then Pi is defined, is proper (as each Qj, j < i, is proper, and by III 3.2) and has a dense subset of power ℵ (by III 4.1). Let Gi ⊆ Pi be generic so clearly there is B ⊆ ω1, such that in V[Gi] every subset of ω1 belongs to L[A, B], The following now follows:
Fact. In V[Gi], every countableN ⥽(H(ℵ2), ∈, A, B) is isomorphic toLβ[A ∩ δ, B ∩ δ] for some β < h(δ), where δ = δ(N) = ω1, ∩ N.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCE
- 1
- Cited by

