Published online by Cambridge University Press: 07 September 2020
In connection with the work of Anscombe, Macpherson, Steinhorn and the present author in [1] we investigate the notion of a multidimensional exact class (R-mec), a special kind of multidimensional asymptotic class (R-mac) with measuring functions that yield the exact sizes of definable sets, not just approximations. We use results about smooth approximation [24] and Lie coordinatization [13] to prove the following result (Theorem 4.6.4), as conjectured by Macpherson: For any countable language 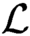 $\mathcal {L}$ and any positive integer d the class
$\mathcal {L}$ and any positive integer d the class 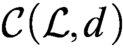 $\mathcal {C}(\mathcal {L},d)$ of all finite
$\mathcal {C}(\mathcal {L},d)$ of all finite 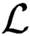 $\mathcal {L}$-structures with at most d 4-types is a polynomial exact class in
$\mathcal {L}$-structures with at most d 4-types is a polynomial exact class in 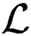 $\mathcal {L}$, where a polynomial exact class is a multidimensional exact class with polynomial measuring functions.
$\mathcal {L}$, where a polynomial exact class is a multidimensional exact class with polynomial measuring functions.
Dedicated to the memories of my son Arthur and my mother Valerie