Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Donder, Hans-Dieter
and
Koepke, Peter
1983.
On the consistency strength of ‘Accessible’ Jonsson Cardinals and of the Weak Chang Conjecture.
Annals of Pure and Applied Logic,
Vol. 25,
Issue. 3,
p.
233.
1984.
Combinatorial Set Theory: Partition Relations for Cardinals.
Vol. 106,
Issue. ,
p.
335.
Shelah, Saharon
1986.
Around Classification Theory of Models.
Vol. 1182,
Issue. ,
p.
224.
Tryba, Jan
1986.
Rowbottom-type properties and a cardinal arithmetic.
Proceedings of the American Mathematical Society,
Vol. 96,
Issue. 4,
p.
661.
Shelah, Saharon
1987.
Classification Theory.
Vol. 1292,
Issue. ,
p.
264.
Shelah, Saharon
1987.
More on powers of singular cardinals.
Israel Journal of Mathematics,
Vol. 59,
Issue. 3,
p.
299.
Shelah, Saharon
and
Stanley, Lee
1987.
A theorem and some consistency results in partition calculus.
Annals of Pure and Applied Logic,
Vol. 36,
Issue. ,
p.
119.
Shelah, Saharon
1988.
Successors of singulars, cofinalities of reduced products of cardinals and productivity of chain conditions.
Israel Journal of Mathematics,
Vol. 62,
Issue. 2,
p.
213.
Donder, Hans-Dieter
and
Levinski, Jean-Pierre
1989.
Some principles related to Chang's conjecture.
Annals of Pure and Applied Logic,
Vol. 45,
Issue. 1,
p.
39.
Burke, Maxim R.
and
Magidor, Menachem
1990.
Shelah's pcf theory and its applications.
Annals of Pure and Applied Logic,
Vol. 50,
Issue. 3,
p.
207.
Jech, Thomas
1995.
Singular Cardinals and the PCF Theory.
Bulletin of Symbolic Logic,
Vol. 1,
Issue. 4,
p.
408.
Pereira, Luís
2007.
Cardinal estimates using a topological approach.
Periodica Mathematica Hungarica,
Vol. 55,
Issue. 2,
p.
149.
Shelah, Saharon
2009.
The Erdős–Rado Arrow for Singular Cardinals.
Canadian Mathematical Bulletin,
Vol. 52,
Issue. 1,
p.
127.
Larson, Jean A.
2012.
Sets and Extensions in the Twentieth Century.
Vol. 6,
Issue. ,
p.
145.
Shelah, Saharon
2012.
PCF arithmetic without and with choice.
Israel Journal of Mathematics,
Vol. 191,
Issue. 1,
p.
1.
Shelah, Saharon
2024.
Pcf without choice Sh835.
Archive for Mathematical Logic,
Vol. 63,
Issue. 5-6,
p.
623.

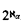 , for ℵ
, for ℵ