Published online by Cambridge University Press: 12 March 2014
Let (M, 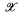 )⊨ ACA0 be such that
)⊨ ACA0 be such that 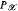 , the collection of all unbounded sets in
, the collection of all unbounded sets in 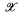 , admits a definable complete ultrafilter and let T be a theory extending first order arithmetic coded in
, admits a definable complete ultrafilter and let T be a theory extending first order arithmetic coded in 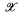 such that M thinks T is consistent. We prove that there is an end-extension N ⊨ T of M such that the subsets of M coded in N are precisely those in
such that M thinks T is consistent. We prove that there is an end-extension N ⊨ T of M such that the subsets of M coded in N are precisely those in 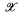 . As a special case we get that any Scott set with a definable ultrafilter coding a consistent theory T extending first order arithmetic is the standard system of a recursively saturated model of T.
. As a special case we get that any Scott set with a definable ultrafilter coding a consistent theory T extending first order arithmetic is the standard system of a recursively saturated model of T.