Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pudlák, Pavel
2008.
Computer Science – Theory and Applications.
Vol. 5010,
Issue. ,
p.
13.
Beckmann, Arnold
2009.
Logic, Language, Information and Computation.
Vol. 5514,
Issue. ,
p.
1.
BECKMANN, ARNOLD
and
BUSS, SAMUEL R.
2009.
POLYNOMIAL LOCAL SEARCH IN THE POLYNOMIAL HIERARCHY AND WITNESSING IN FRAGMENTS OF BOUNDED ARITHMETIC.
Journal of Mathematical Logic,
Vol. 09,
Issue. 01,
p.
103.
Beyersdorff, Olaf
2009.
On the correspondence between arithmetic theories and propositional proof systems – a survey.
Mathematical Logic Quarterly,
Vol. 55,
Issue. 2,
p.
116.
Krajíček, Jan
2010.
Computer Science Logic.
Vol. 6247,
Issue. ,
p.
22.
Krajíček, Jan
2011.
A note on propositional proof complexity of some Ramsey-type statements.
Archive for Mathematical Logic,
Vol. 50,
Issue. 1-2,
p.
245.
Pollett, Chris
2011.
Conservative fragments of $${{S}^{1}_{2}}$$ and $${{R}^{1}_{2}}$$.
Archive for Mathematical Logic,
Vol. 50,
Issue. 3-4,
p.
367.
Thapen, Neil
2011.
Higher complexity search problems for bounded arithmetic and a formalized no-gap theorem.
Archive for Mathematical Logic,
Vol. 50,
Issue. 7-8,
p.
665.
Kołodziejczyk, Leszek Aleksander
Nguyen, Phuong
and
Thapen, Neil
2011.
The provably total NP search problems of weak second order bounded arithmetic.
Annals of Pure and Applied Logic,
Vol. 162,
Issue. 6,
p.
419.
Arai, Toshiyasu
2011.
Nested PLS.
Archive for Mathematical Logic,
Vol. 50,
Issue. 3-4,
p.
395.
Pudlák, Pavel
and
Thapen, Neil
2012.
Alternating minima and maxima, Nash equilibria and Bounded Arithmetic.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 5,
p.
604.
Beckmann, Arnold
Pudlák, Pavel
and
Thapen, Neil
2014.
Parity Games and Propositional Proofs.
ACM Transactions on Computational Logic,
Vol. 15,
Issue. 2,
p.
1.
Beckmann, Arnold
and
Razafindrakoto, Jean-José
2017.
Logic, Language, Information, and Computation.
Vol. 10388,
Issue. ,
p.
31.
Beckmann, Arnold
and
Buss, Sam
2017.
The NP Search Problems of Frege and Extended Frege Proofs.
ACM Transactions on Computational Logic,
Vol. 18,
Issue. 2,
p.
1.
Goldberg, Paul W.
and
Papadimitriou, Christos H.
2018.
Towards a unified complexity theory of total functions.
Journal of Computer and System Sciences,
Vol. 94,
Issue. ,
p.
167.
Pudlák, Pavel
and
Thapen, Neil
2019.
Random resolution refutations.
computational complexity,
Vol. 28,
Issue. 2,
p.
185.
Krajíček, Jan
2019.
Proof Complexity.
Müller, Moritz
2021.
Typical forcings, NP search problems and an extension of a theorem of Riis.
Annals of Pure and Applied Logic,
Vol. 172,
Issue. 4,
p.
102930.
Kołodziejczyk, Leszek Aleksander
and
Thapen, Neil
2022.
Approximate counting and NP search problems.
Journal of Mathematical Logic,
Vol. 22,
Issue. 03,
Akbar Tabatabai, Amirhossein
2022.
Logic, Language, Information, and Computation.
Vol. 13468,
Issue. ,
p.
378.

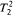 and
and 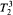 .
.