It is well known that many statements provable from combinatorial principles true in the constructible universe L can also be shown to be consistent with ZFC by forcing. Recent work by Shelah and Stanley [4] and the author [5] has clarified the relationship between the axiom of constructibility and forcing by providing Martin's Axiom-type forcing axioms equivalent to ◊ and the existence of morasses. In this paper we continue this line of research by providing a forcing axiom equivalent to □κ. The forcing axiom generalizes easily to inaccessible, non-Mahlo cardinals, and provides the motivation for a corresponding generalization of □κ.

In order to state our forcing axiom, we will need to define a strategic closure condition for partial orders. Suppose P = 〈P, ≤〉 is a partial order. For each ordinal α we will consider a game 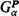played by two players, Good and Bad. The players choose, in order, the terms in a descending sequence of conditions 〈pβ∣β < α〉 Good chooses all terms pβ for limit β, and Bad chooses all the others. Bad wins if for some limit β<α, Good is unable to move at stage β because 〈pγ∣γ < β〉 has no lower bound. Otherwise, Good wins. Of course, we will be rooting for Good.